小学六年级奥数专项训练：第14讲：应用题（二） 教学课件PPT

这是一份小学六年级奥数专项训练：第14讲：应用题（二） 教学课件PPT，共16页。PPT课件主要包含了应用题二，年龄差不变，年龄差，－6＝28岁，－7＝28岁，定价占成本的百分比，＋20%，打八八折后，＝1500元，＝0056等内容，欢迎下载使用。

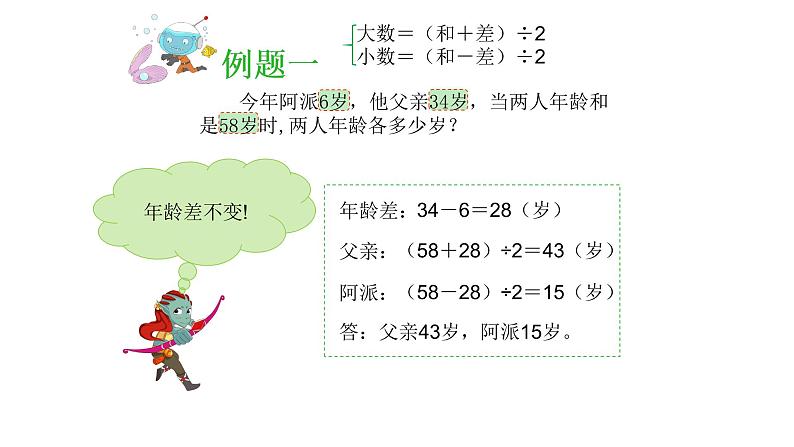
今年阿派6岁，他父亲34岁，当两人年龄和是58岁时,两人年龄各多少岁？
（58＋28）÷2＝43（岁）
（58－28）÷2＝15（岁）
答：父亲43岁，阿派15岁。
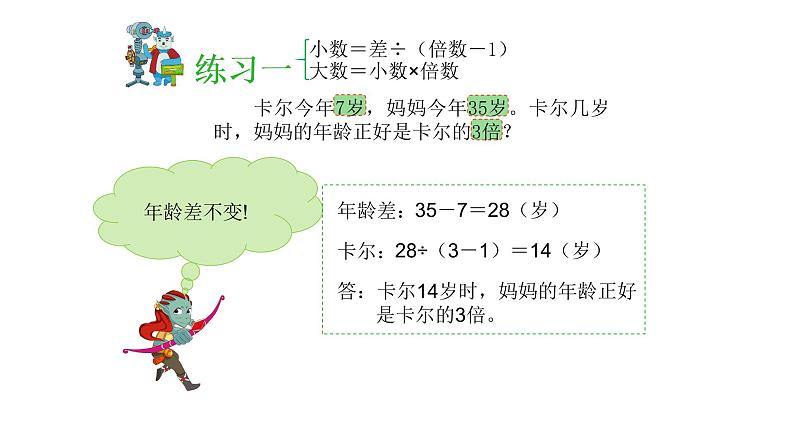
卡尔今年7岁，妈妈今年35岁。卡尔几岁时，妈妈的年龄正好是卡尔的3倍？
28÷（3－1）＝14（岁）
答：卡尔14岁时，妈妈的年龄正好 是卡尔的3倍。
某商品按20%利润定价，然后按八八折卖出，共获得利润84元，这件商品的成本是多少元？
（1＋20%）×88%
新定价的利润占成本百分比：
（1＋20%）×88%－1
答：这件商品的成本是1500元。
旧定价占成本的百分比：
某商品按定价的80%出售，仍可获得20%的利润，定价时期望的利润是百分之几？
新定价占成本的百分比：
答：定价时期望的利润是50%。
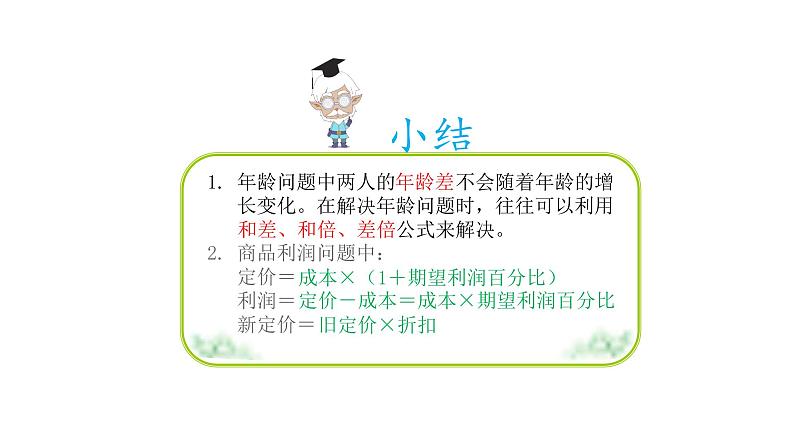
2. 商品利润问题中： 定价＝ 利润＝ 新定价＝
1. 年龄问题中两人的 不会随着年龄的增 长变化。在解决年龄问题时，往往可以利用 公式来解决。
成本×（1＋期望利润百分比）
定价－成本＝成本×期望利润百分比
阿博士将16000元存入银行，定期2年，年利率是2.25%，问到期后阿博士能拿回本息共多少元？
利息＝本金×利率×时间
16000×2.25%×2
答：到期后博士能拿回本息16720元。
288÷1200÷0.8%
答：存款期为30个月。
欧拉存入银行1200元，月利率0.8%，到期后连本带利共取出1488元，求存款期多长？
时间＝利息÷本金÷利率
一列火车经过南京长江大桥，大桥长6700米，这列火车长140米，火车每分钟行400米，这列火车通过长江大桥需要多少分钟？
答：这列火车通过长江大桥需要17.1分钟。
一列火车通过360米的第一个隧道用了24秒钟，接着通过第二个长216米的隧道用了16秒钟，求这列火车的长度。
答：这列火车的长度是72米。
轮船以相同的速度航行，从A城到B城需3天，从B城到A城需4天。小筏从A城漂到B城需几天？
假设A城到B城的距离为12千米。
12÷3＝4（千米/天）
12÷4＝3（千米/天）
（4-3）÷2＝0.5（千米/天）
答：小筏从A城漂到B城需24天。
12÷0.5＝24（天）
已知一艘轮船顺水行48千米需4小时，逆水行48千米需6小时。现在轮船从上游A港到下游B港，已知两港间的水路长为72千米，开船时有一游客从窗口扔到水里一块木板，问船到B港时，木板离B港还有多远？
48÷4＝12（千米/小时）
48÷6＝8（千米/小时）
（12－8）÷2＝2（千米/小时）
答：木板离B港还有60千米。
72÷12＝6（小时）
72－2×6＝60（千米）