中考数学全程复习方略 第11讲 一次函数 课件

这是一份中考数学全程复习方略 第11讲 一次函数 课件，共56页。PPT课件主要包含了ykx+b，ykx，一次函数的图象，待定系数法，解析式，-2x2，自变量的，取值范围，函数值等内容，欢迎下载使用。

考点一　一次函数的图象和性质【主干必备】1.一次函数与正比例函数的概念
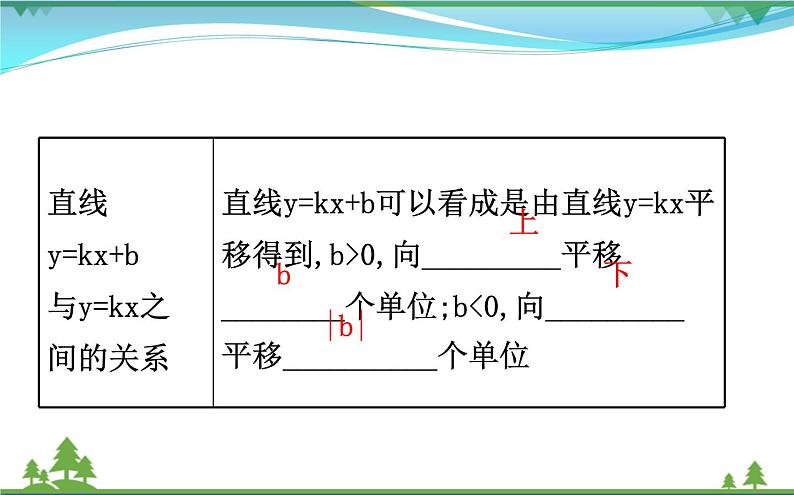
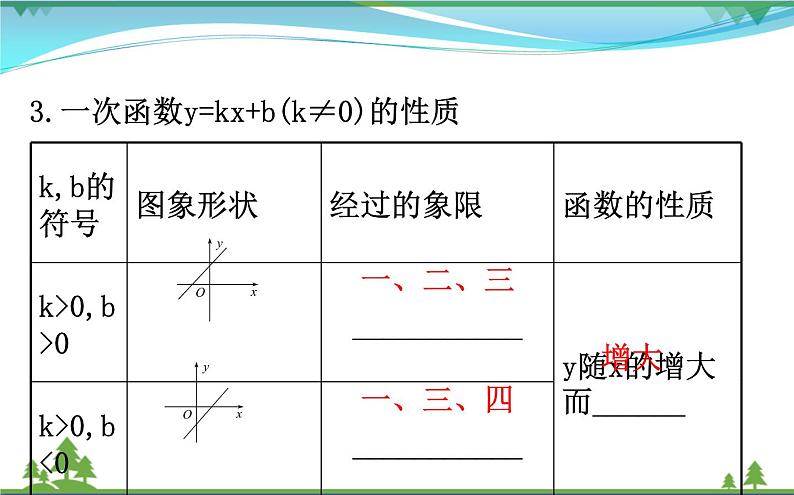
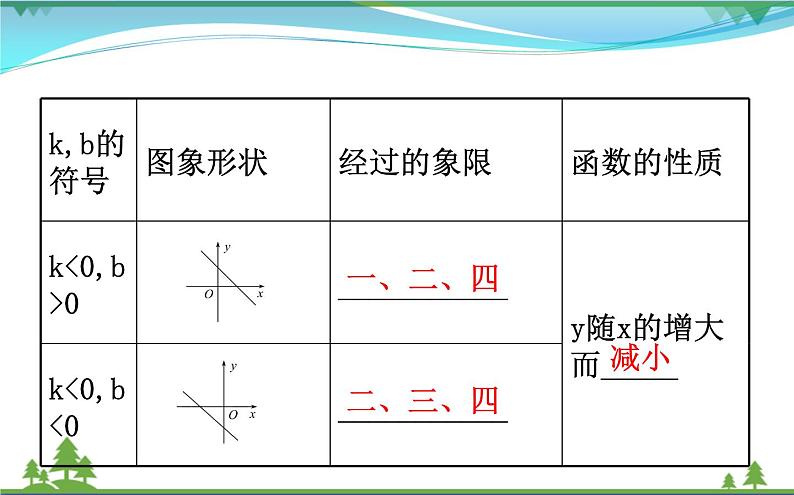
3.一次函数y=kx+b(k≠0)的性质
【微点警示】当两个函数y1=k1x+b1(k1≠0)与y2=k2x+b2(k2≠0)所在直线平行时⇔k1=k2,b1≠b2.
【核心突破】例1(1)(2019·临沂中考)下列关于一次函数y=kx+b (k<0,b>0)的说法,错误的是(　 　)A.图象经过第一、二、四象限B.y随x的增大而减小C.图象与y轴交于点(0,b)D.当x>- 时,y>0
(2)(2019·潍坊中考)当直线y=(2-2k)x+k-3经过第二、三、四象限时,则k的取值范围是____________. 
【明·技法】1.已知k的符号,可以确定函数值随着自变量增大而变化的规律;反之,已知函数值随着自变量的增大而变化的规律,可以推测k的符号.当函数值随着自变量的增大而增大时,k>0;当函数值随着自变量的增大而减小时,k<0.
2.|k|的大小决定直线的倾斜程度,即|k|越大,直线与x轴相交所成的锐角越大,y随x变化越快;|k|越小,直线与x轴相交所成的锐角越小,y随x变化越慢.
【题组过关】1.(2019·杭州中考)已知一次函数y1=ax+b和y2=bx+a (a≠b),函数y1和y2的图象可能是(　 　)
2.(2019·广州一模)已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数的图象的交点在(　 　)A.第一象限　　　　　B.第二象限C.第三象限D.第四象限
3.(2019·天津中考)直线y=2x-1与x轴的交点坐标为_________. 4.(2019·成都简阳期末)已知一次函数y=(-3a+1)x+a的图象上两点A(x1,y1),B(x2,y2),当x1>x2时,有y1考点二　一次函数解析式的确定【主干必备】一次函数解析式的确定方法及步骤
【核心突破】例2(2019·盐城中考)如图,在平面直角坐标系中,一次函数y=2x-1的图象分别交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是__________. 
【明·技法】用待定系数法求一次函数解析式时对特殊点的利用(1)与y轴的交点:一次函数图象与y轴交点的纵坐标的值即一次函数y=kx+b中b的值,可直接代入.(2)与x轴的交点:若一次函数图象与x轴交点为(x,0),则代入可建立方程kx+b=0.
【题组过关】1.(2019·绍兴中考)若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于(　 　)A.-1　　　　B.0　　　　C.3　　　　D.4
2.(2019·乐山中考)如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(-1,a).(1)求直线l1的解析式.(2)求四边形PAOC的面积.
【解析】(1)∵点P(-1,a)在直线l2:y=2x+4上,∴2×(-1)+4=a,即a=2,则点P的坐标为(-1,2),设直线l1的解析式为:y=kx+b(k≠0),那么 解得: ∴直线l1的解析式为y=-x+1.
(2)∵直线l1与y轴相交于点C,∴C的坐标为(0,1),又∵直线l2与x轴相交于点A,∴A点的坐标为(-2,0),则AB=3,而S四边形PAOC=S△PAB-S△BOC,∴S四边形PAOC= ×3×2- ×1×1= .
3.(2019·广州一模)如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与直线AD交于点A ,点D的坐标为(0,1).(1)求直线AD的解析式.
(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
考点三　一次函数与方程(组)、不等式的关系【主干必备】一次函数与方程(组)、不等式的关系
【微点警示】一次函数与方程(组)、不等式的关系问题一定要结合图象去解决,即数形结合.
【核心突破】例3(1)(2019·滨州中考)如图,直线y=kx+b(k<0)经过点A(3,1),当kx+b< x时,x的取值范围为__________. 
(2)(2018·白银中考)如图,一次函数y=-x-2与y=2x+m的图象相交于点P(n,-4),则关于x的不等式组 的解集为_____________. 
【明·技法】解答一次函数与方程、不等式的题目的三点注意(1)要明确一次函数、一次方程和一元一次不等式的内在联系.(2)在观察图象时,特别注意直线与x轴的交点以及两直线的交点.
(3)要做到数形结合.这类题目中自变量的取值通常在给定的两个点的横坐标之间.
【题组过关】1.(2019·安庆桐城期末)已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是(　 　)
2.(2019·河南一模)一次函数y=-3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥-3x+b的解集在数轴上表示正确的是(　 　)
3.(2019·南通二模)已知直线y=-x+2与直线y=2x+6相交于点A,与x轴分别交于C,B两点,若点D 落在△ABC内部(不含边界),则a的取值范围是世纪金榜导学号(　 　)A.-34.(2019·榆林期末)如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组 的解是_______. 
考点四　一次函数的应用【主干必备】一次函数的实际应用
【微点警示】解决分段函数问题时,各段自变量做到不重不漏,注意每段自变量的取值范围.
【核心突破】例4(2019·河南中考)学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5个A奖品和4个B奖品共需210元.(1)求A,B两种奖品的单价.
(2)学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的 .请设计出最省钱的购买方案,并说明理由.
【思路点拨】(1)根据两个等量关系:①3个A奖品+2个B奖品=120元;②5个A奖品+4个B奖品=210元,列出方程组求解即可.
(2)设购买A奖品z个,购买奖品的花费为W元,根据“A奖品的数量不少于B奖品数量的 ”列出关于z的不等式,求出其解集;根据(1)中的结论并结合题意列出W关于z的一次函数解析式,最后根据自变量的取值范围和一次函数的性质求解即可.
【自主解答】(1)设A的单价为x元,B的单价为y元,根据题意,得 ∴A的单价为30元,B的单价为15元.
(2)设购买A奖品z个,则购买B奖品为(30-z)个,购买奖品的花费为W元,由题意可知,z≥ (30-z),∴z≥ ,W=30z+15(30-z)=450+15z,当z=8时,W有最小值为570元,即购买A奖品8个,购买B奖品22个,花费最少.
【明·技法】应用一次函数知识解决实际问题常见的两种模式(1)建立函数模型,然后借助方程或不等式或函数图象来解决问题.
(2)利用一次函数的图象的性质,如增减性等来解决生活中的最优化问题,它常与方程(组)或不等式(组)一起考查.
【题组过关】1.(2019·山西中考)某游泳馆推出了两种收费方式.方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).(1)请分别写出y1,y2与x之间的函数表达式.(2)小亮一年内在此游泳馆游泳的次数x在什么范围时,选择方式一比方式二省钱.
【解析】(1)y1=30x+200;y2=40x.(2)由y120,∴当x>20时选择方式一比方式二省钱.
2.(2019·重庆南岸区模拟)蓝莓果实中含有丰富的营养成分,经常食用蓝莓制品,还可明显地增强视力,消除眼睛疲劳,某蓝莓种植生产基地产销两旺,当天采摘的蓝莓部分加工成蓝莓汁销售(按1斤蓝莓加工成1斤蓝莓汁计算),剩下的部分直接销售,且当天加工的蓝莓汁以及剩余的蓝莓都能在当天全部售出,3斤蓝莓与2斤蓝莓
汁的售价是580元,4斤蓝莓与3斤蓝莓汁的售价是840元.已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤蓝莓或加工35斤蓝莓汁.
(1)请问购买1斤蓝莓多少元?购买1斤蓝莓汁多少元?(2)设安排x名工人采摘蓝莓,剩下的工人加工蓝莓汁,基地应如何分配工人,才能使一天的销售额最大?并求出最大销售额.
【解析】(1)设购买1斤蓝莓m元,购买1斤蓝莓汁n元,根据题意得: 解得: 则购买1斤蓝莓60元,购买1斤蓝莓汁200元.
(2)设安排x名工人采摘蓝莓,剩下的(20-x)名工人加工蓝莓汁,销售额为w元,根据题意得:w=70x×60+35×(20-x)×200=4 200x+140 000-7 000x=-2 800x+140 000,∵-2 800<0,∴w随x的增大而减小,∵70x≥35(20-x),