第五单元 第13课时 平面直角坐标系（含答案）

这是一份第五单元 第13课时 平面直角坐标系（含答案），共29页。PPT课件主要包含了小题热身，图13－1，考点管理，x为任意实数y＝0，x＝0y为任意实数，x0y0，横坐标与纵坐标相等，x＋ay，xy＋b，xy－b等内容，欢迎下载使用。

1．在平面直角坐标系中，点P(－2，－3)所在的象限是(　 　)A．第一象限 B．第二象限C．第三象限 D．第四象限2．若将点A(1，3)向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为 (　 　)A．(2，－1) B．(－1，0)C．(－1，－1) D．(－2，0)
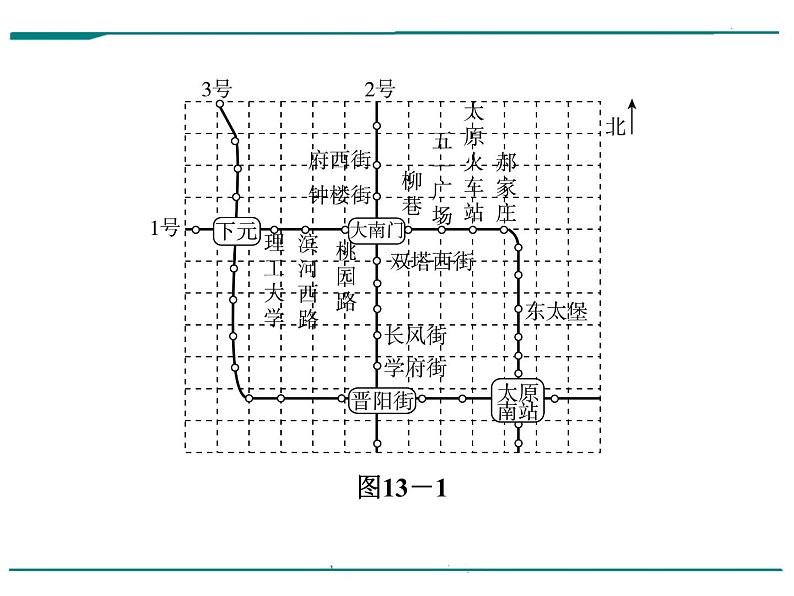
3．点A(3，－2)关于x轴对称的点的坐标是_________．4．如图13－1是利用网格画出的太原市地铁1，2，3号线路部分规划示意图．若建立适当的平面直角坐标系，表示双塔西街点的坐标为(0，－1)，表示桃园路的点的坐标为(－1，0)，则表示太原火车站的点(正好在网格点上)的坐标是__________．
一、必知6 知识点1．平面直角坐标系坐标平面内的点与有序实数对是________对应的．x轴，y轴上的点不属于任何象限．点P(x，y)在x轴上⇔______________________；点P(x，y)在y轴上⇔____________________；点P(x，y)既在x轴上，又在y轴上⇔x，y同时为零，即点P的坐标为(0，0)．
平面内点的坐标的特征：点P(x，y)在第一象限⇔____________；点P(x，y)在第二象限⇔____________；点P(x，y)在第三象限⇔____________；点P(x，y)在第四象限⇔____________．2．平面直角坐标系内点的坐标特征平行于x轴(或垂直于y轴)的直线上的点：纵坐标相同，横坐标为不相等的实数；平行于y轴(或垂直于x轴)的直线上的点：横坐标相同，纵坐标为不相等的实数．
【智慧锦囊】各象限角平分线上的点的坐标特征：(1)第一、三象限角平分线上的点______________________；(2)第二、四象限角平分线上的点__________________________ __．
横坐标与纵坐标互为相反数
3．点与坐标轴的距离(1)点P(a，b)到x轴的距离等于______；(2)点P(a，b)到y轴的距离等于______．4．平面直角坐标系中的平移点的平移：在平面直角坐标系中，将点(x，y)向右或向左平移a个单位，可以得到的对应点是_____________或______ _______；将点(x，y)向上或向下平移b个单位，可以得到的对应点____________或____________．图形的平移：对于一个图形平移，这个图形上所有点的坐标都要发生相应的变化，反过来，从图形上的点的坐标的某种变化也可以看出对这个图形进行了怎样的平移．
5．平面直角坐标系中的对称点的坐标对称点的坐标的特征：点P(x，y)关于x轴对称的点P1的坐标为___________；关于y轴对称的点P2的坐标为__________ __；关于原点对称的点P3的坐标为______________．
【智慧锦囊】(1)点的平移口诀：右加左减，上加下减；(2)点的对称口诀：关于x轴对称横等纵反，关于y轴对称横反纵等，关于原点对称横反纵反．
6．用坐标表示地理位置确定位置的方法主要有两种：(1)横纵交错法，由交点的唯一性确定点的位置；(2)方位角＋距离．
二、必会2 方法1．确定点在坐标系中的位置的方法根据问题中的已知条件，判断横坐标、纵坐标是大于0，等于0，还是小于0.2．数形结合思想数形结合是重要的数学思想，已知点的坐标可以确定点在坐标系中的位置，反过来已知点的位置，可以确定其坐标，这就是数形结合思想．
坐标平面内的点的坐标特征 　在平面直角坐标系中，点P(m－3，4－2m)不可能在 (　 　)A．第一象限 B．第二象限C．第三象限 D．第四象限【解析】 ①m－3＞0，即m＞3时，－2m＜－6，4－2m＜－2，∴点P(m－3，4－2m)在第四象限；②m－3＜0，即m＜3时，－2m＞－6，4－2m＞－2，∴点P(m－3，4－2m)可以在第二或三象限，综上所述，点P不可能在第一象限．
1．已知点P(0，m)在y轴的负半轴上，则点M(－m，－m＋1)在 (　 　)A．第一象限 B．第二象限C．第三象限 D．第四象限【解析】 ∵点P(0，m)在y轴的负半轴上，∴m<0，∴点M(－m，－m＋1)在第一象限
2．点P(x－2，x＋3)在第一象限，则x的取值范围________．【点悟】　解决此类问题的一般方法是根据点在坐标系中的符号特征，建立不等式(组)或者方程(组)，把点的问题转化为不等式(组)或方程(组)来解决．
平面直角坐标系中的平移、旋转与对称 　如图13－2所示，三架飞机P，Q，R保持编队
飞行，某时刻在坐标系中的坐标分别为(－1，1)，(－3，1)，(－1，－1)，30 s后，飞机P飞到P′(4，3)位置，则飞机Q，R的位置Q′，R′分别为 (　 　)A．Q′(2，3)，R′(4，1)B．Q′(2，3)，R′(2，1)C．Q′(2，2)，R′(4，1)D. Q′(3，3)，R′(3，1)
【解析】 由点P(－1，1)到P′(4，3)知，编队需向右平移5个单位、向上平移2个单位，∴点Q(－3，1)的对应点Q′坐标为(2，3)，点R(－1，－1)的对应点R′坐标为(4，1)．
1．如图13－3，点A，B的坐标分别为(2，0)，(0，1)，若将线段AB平移至A1B1，则a＋b的值为 (　 　)A．2 B．3C．4 D．5 
【解析】 由点B平移前后的纵坐标分别为1，2，可得点B向上平移了1个单位，由点A平移前后的横坐标分别为2，3，可得点A向右平移了1个单位，由此得线段AB的平移的过程是：向上平移1个单位，向右平移1个单位，点A，B均按此规律平移，由此可得a＝0＋1＝1，b＝0＋1＝1，故a＋b＝2.
2．在平面直角坐标系中，把点A(2，3)向左平移一个单位得到点A′，则点A′的坐标为__________．【解析】 ∵点A(2，3)向左平移1个单位长度，∴点A′的横坐标为2－1＝1，纵坐标不变，∴A′的坐标为(1，3)．
3．如图13－4，在平面直角坐标系中，Rt△ABC的三个顶点分别是A(－3，1)，B(0，3)，C(0，1)．(1)将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1；(2)分别连结AB1，BA1后，求四边形AB1A1B的面积．
解： (1)如答图所示；
【点悟】　(1)求一个图形旋转、平移后的图形对应点的坐标，一般要把握三点：一是根据图形变换的性质；二是利用图形的全等关系；三是确定点所在的象限；(2)平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．
平面直角坐标系中点的规律探究 　把多块大小不同的30°直角三角板如图13－5所示摆放在平面直角坐标系中，第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0，1)，∠ABO＝30°；第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1；第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2；第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3；…按此规律继续下去，则点B2 017的坐标为_____________.
1．如图13－6，在平面直角坐标系中，每个最小方格的边长均为1个单位长度，P1，P2，P3，…均在格点上，其顺序按图中“→”方向排列，如：P1(0，0)，P2(0，1)，P3(1，1)，P4(1，－1)，P5(－1，－1)，P6(－1，2)，…根据这个规律，点P2 016的坐标为________________．
【解析】 根据各个点的位置关系，可得出下标数为4的倍数的点在第四象限的角平分线上，下标数被4除余1的点在第三象限，下标数被4除余2的点在第二象限的角平分线上，下标数被4除余3的点在第一象限的角平分线上，2 016为4的倍数，则点P2 016的在第四象限的角平分线上，且横纵坐标的绝对值为2 016÷4＝504，∴点P2 016的坐标为(504，－504)．
2．如图13－7，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次不断地移动，每次移动一个单位，得到点A1(0，1)，A2(1，1)，A3(1，0)，A4(2，0)，…那么点A4n＋1(n是自然数)的坐标为__________ __．
【解析】 ∵n＝1时，4×1＋1＝5，点A5(2，1)，n＝2时，4×2＋1＝9，点A9(4，1)，n＝3时，4×3＋1＝13，点A13(6，1)，…∴点A4n＋1的坐标为(2n，1)．
必明3 易错点1．注意点的坐标与该点到坐标轴的距离的关系，不要把它们混淆；2．坐标系中点的平移，注意平移方向不要弄反；3．关于x轴与y轴的坐标特征不要弄错．