





华师大版八年级下册第17章 函数及其图象17.1 变量与函数多媒体教学ppt课件
展开变量与函数
大千世界处在不停的运动变化之中,如何 来研究这些运动变化并寻找规律呢?数学上常用变量与函数来刻画各种运动变化.
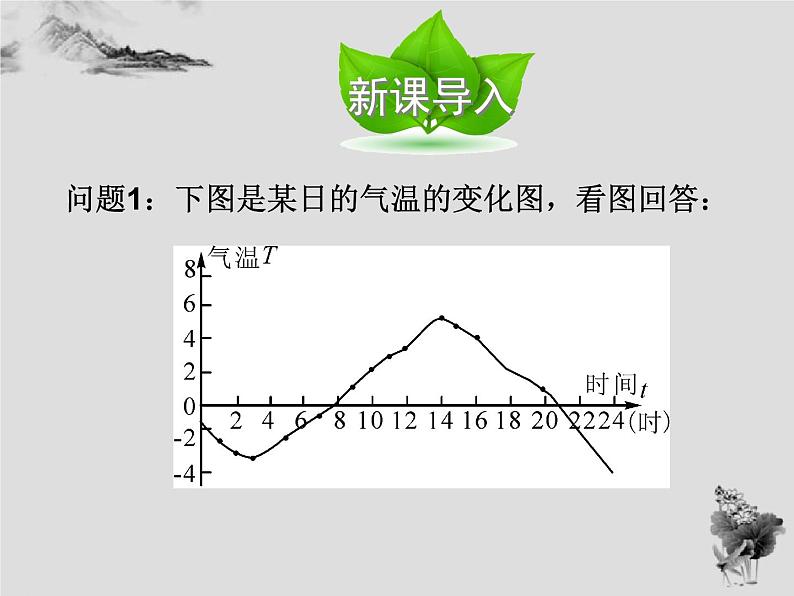
问题1:下图是某日的气温的变化图,看图回答:
1.这天的6时、10时和14时的气温分别是多少?任意给出这天中的某一时刻,你能否说出这一时刻的气温是多少吗?2.这一天中,最高气温是多少?最低气温是多少?3.这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
从图中我们可以看出,随着时间t(时)的变化,相应的气温T(℃)也随之变化.
观察上表,说一说随着年龄的增长,小蕾的体重是如何变化的?在哪一段时间内体重的增加较快?
问题2:小蕾在过14岁生日的时候,看到了爸爸为她记录的各周岁时的体重(kg),如下表:
从图中我们可以看出,随着周岁的变化,相应的体重也随之变化.
问题3:收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:
细心的同学可能会发现: l 与 f 的乘积是一个定值,即 说明波长越大,频率f 就____________
l ·f = 30000
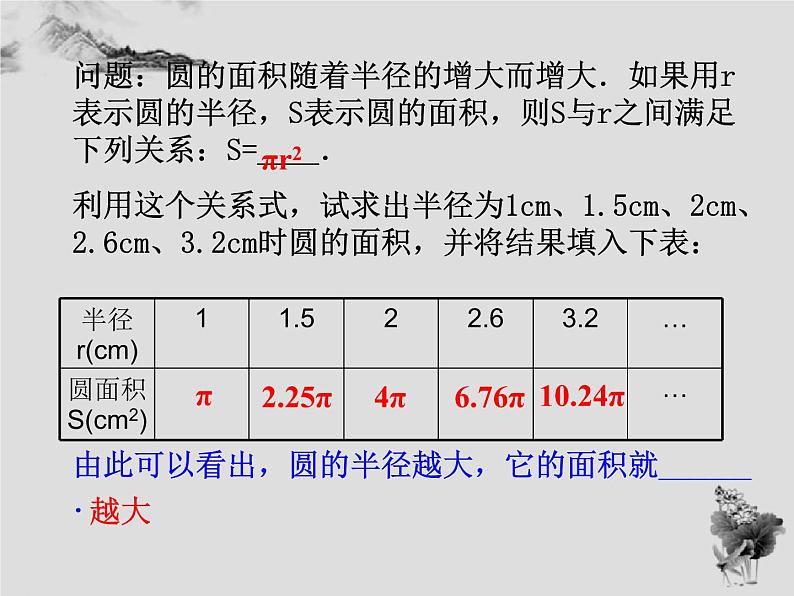
利用这个关系式,你能算出半径为1 cm、1.5 cm、2 cm、2.6 cm、3.2 cm时圆的面积吗?
问题4:圆的面积随着半径的增大而增大,如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=πr2.
问题:圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=____.利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积,并将结果填入下表:由此可以看出,圆的半径越大,它的面积就______.
在上述问题中分别有几个量?分别指出每个问题中的各个量.
在第1个问题中,有两个变量,一个是时间,另一个是温度,温度随着时间的变化而变化.在第2个问题中,有两个变量,一个是年龄,另一个是体重,体重随着年龄的变化而变化.
在第3个问题中,λ和f是变量,而它们的积等于300 000,是常量.在第4个问题中,S和r都是变量,π和2都是常量.
常量:在某一变化过程中始终保持不变的量称为常量.变量:在某一变化过程中可以取不同数值的量叫做变量.
大家举例说一说哪些是常量和变量?
一般地,如果在一个变化过程中,有两个变量,假设为x与y,对于x的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是因变量,此时也称y是x的函数.
日常生活和自然界中函数关系的例子很多。请大家举一些函数关系的例子
上述的第3个问题中,λf=300 000,给出一个f的值,变量λ有唯一值与之对应,f是自变量,λ是因变量(λ是f的函数).上述的第4个问题中,S=πr2,给出变量r的一个值,便可以得到变量S的唯一值和它对应,r是自变量,S是因变量(S是r的函数).
练一练:判断下列变量关系是不是函数?
(1)等腰三角形的底边长与面积
判断是不是函数,我们可以看它的数学式子中的变量之间是否满足函数的定义
表示函数关系的方法通常有三种:(1)解析法,如问题3中的f=300000/λ,问题4中的S=πr2,这些表达式称为函数的关系式.(2)列表法,如问题2中的小蕾的体重表,问题3中的波长与频率关系表.(3)图象法,如问题1中的气温曲线.
1、先认真审题,根据题意找出相等关系
2、按相等关系,写出含有两个变量的等式
3、将等式变形为用含有自变量的代数式表示函数的式子
函数的关系式是等式,通常等式的右边是含有自变量的代数式,左边的一个字母表示函数。例如: S=πr2 y=0.50x y=2.4x+0.2
例1用总长60 m的篱笆围成矩形场地,求矩形面积S(m2)与边l (m)之间的关系式,并指出式中的常量和变量,自变量与函数.
面积和总长是常量,边长是变量.
下列关系式中,哪些式中的y是x的函数?
(1)和(3)中的y是x的函数.
求当x=5时,各个函数的函数值.
1.常量和变量在研究“某一变化过程中”时是确定的,以s=vt为例(t为时间,v为速度,s为路程):①若速度v固定,则常量是_______,变量是_______;②若时间t固定,则常量是_______,变量是_______.
分析:①速度v固定,即在这个变化过程中v的取值保持不变,此时s随t的变化而变化,可以取不同的数值,故v为常量,s和t为变量;②t固定,即为常量,此时s和v可以取不同的数值,是变量.解:①v,s、t;②t,s、v
2.当x=-2和x=3时,分别求出下列函数的函数值:
(1)当x=-2时,y=-1.5;当x=3时,y=11.
(2)当x=-2时,y=4;当x=3时,y=4.
2.已知变量x与y的四种关系:y=︱x︱,︱y︱=x,2x2-y=0,2x-y2=0其中y是x的函数的有_____个.
分析:依函数定义,︱y︱=x与2x-y2=0中,x每取一个大于0的值,y都有两个与之对应,例如x=4时,︱y︱=4,有y=±4,故y不是x的函数;只有y=︱x︱和2x2-y=0中y是x的函数.解:2
3.若一辆汽车以50千米/时的速度匀速行驶,则行驶的路程s(千米)与行驶的时间t(时)之间的函数关系式是( )A.s=50+50t B.s=50tC.s=50-50t D.以上都不对
4.下列变量间的关系不是函数关系的是( )A.长方形的宽一定,其长与面积B.正方形的周长与面积C.圆的半径与面积D.等腰三角形的底边长与面积
5.下列说法不正确的是( )A.公式V=4/3πr3中,4/3是常量,r是变量,V是πr的函数B.公式V=4/3πr3中,V是r的函数C.公式v=s/t中,v可以是变量,也可以是常量D.圆的面积S是半径r的函数
将t=8代入s=10t+2t2 ,得s=208.所以坡长为208米.
6.一架雪橇沿一斜坡滑下,经过时间t (秒)滑下的路程s(米)由下式给出:s=10t+2t2 .假如从坡顶滑到坡底的时间为8秒,试问坡长为多少?
1.关于函数的定义的理解应注意两个方面,其一是变化过程中有且只有两个变量,其二是对于其中一个变量的每一个值,另一个变量都有唯一的值与它对应.
数学华师大版17.1 变量与函数作业课件ppt: 这是一份数学华师大版17.1 变量与函数作业课件ppt,共10页。PPT课件主要包含了金额数量单价等内容,欢迎下载使用。
华师大版八年级下册17.1 变量与函数教学演示ppt课件: 这是一份华师大版八年级下册17.1 变量与函数教学演示ppt课件,共31页。PPT课件主要包含了不能确定,-32m,-41m,y5-xm,问题1,问题2,问题3,问题4,m×1=50m,m×2100m等内容,欢迎下载使用。
华师大版八年级下册17.1 变量与函数课前预习ppt课件: 这是一份华师大版八年级下册17.1 变量与函数课前预习ppt课件,共28页。PPT课件主要包含了1变量与函数,第1课时变量与函数,-1℃,-4℃,温度升高,温度降低,或者说,πr2,25π,76π等内容,欢迎下载使用。













