- 中考总复习:圆综合复习--知识讲解(提高) 试卷 7 次下载
- 中考总复习:图形的变化--巩固练习(基础) 试卷 1 次下载
- 中考总复习:图形的变化--巩固练习(提高) 试卷 1 次下载
- 中考总复习:图形的变换--知识讲解(提高) 试卷 2 次下载
- 中考总复习:统计与概率--巩固练习 试卷 3 次下载
中考总复习:图形的变换--知识讲解(基础)
展开【考纲要求】
1.通过具体实例认识轴对称、平移、旋转,探索它们的基本性质;
2.能够按要求作出简单平面图形经过轴对称、平移、旋转后的图形,能作出简单平面图形经过一次或两次轴对称后的图形;
3.探索基本图形(等腰三角形、矩形、菱形、等腰梯形、正多边形、圆)的轴对称性质及其相关性质.
4.探索图形之间的变换关系(轴对称、平移、旋转及其组合);
5.利用轴对称、平移、旋转及其组合进行图案设计;认识和欣赏轴对称、平移、旋转在现实生活中的应用.
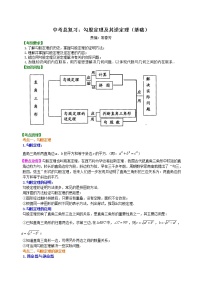
【知识网络】
【考点梳理】
考点一、平移变换
1. 平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,平移不改变图形的形状和大小.
【要点诠释】
(1)平移是运动的一种形式,是图形变换的一种,本讲的平移是指平面图形在同一平面内的变换;
(2)图形的平移有两个要素:一是图形平移的方向,二是图形平移的距离,这两个要素是图形平移的依据;
(3)图形的平移是指图形整体的平移,经过平移后的图形,与原图形相比,只改变了位置,而不改变图形的大小,这个特征是得出图形平移的基本性质的依据.
2.平移的基本性质:由平移的概念知,经过平移,图形上的每一个点都沿同一个方向移动相同的距离,平移不改变图形的形状和大小,因此平移具有下列性质:经过平移,对应点所连的线段平行且相等,对应角相等.
【要点诠释】
(1)要注意正确找出“对应线段,对应角”,从而正确表达基本性质的特征;
(2)“对应点所连的线段平行且相等”,这个基本性质既可作为平移图形之间的性质,又可作为平移作图的依据.
考点二、轴对称变换
1.轴对称与轴对称图形
轴对称:把一个图形沿着某一条直线折叠,如果能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也叫做这两个图形成轴对称,这条直线叫做对称轴,折叠后重合的对应点,叫做对称点.
轴对称图形:把一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
2.轴对称变换的性质
①关于直线对称的两个图形是全等图形.
②如果两个图形关于某直线对称,对称轴是对应点连线的垂直平分线.
③两个图形关于某直线对称,如果它们对应线段或延长线相交,那么交点在对称轴上.
④如果两个图形的对应点连线被同一直线垂直平分,那么这两个图形关于这条直线对称.
3.轴对称作图步骤
①找出已知图形的关键点,过关键点作对称轴的垂线,并延长至2倍,得到各点的对称点.
②按原图形的连结方式顺次连结对称点即得所作图形.
考点三、旋转变换
1.旋转概念:把一个图形绕着某一点O转动一个角度的图形变换叫做旋转.点O叫做旋转中心,转动的角叫做旋转角.
2.旋转变换的性质
图形通过旋转,图形中每一点都绕着旋转中心沿相同的方向旋转了同样大小的角度,任意一对对应点与旋转中心的连线都是旋转角,对应点到旋转中心的距离相等,对应线段相等,对应角相等,旋转过程中,图形的形状、大小都没有发生变化.
3.旋转作图步骤
①分析题目要求,找出旋转中心,确定旋转角.
②分析所作图形,找出构成图形的关键点.
③沿一定的方向,按一定的角度、旋转各顶点和旋转中心所连线段,从而作出图形中各关键点的对应点.
④ 按原图形连结方式顺次连结各对应点.
4.中心对称与中心对称图形
中心对称:
把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心对称的对称点.
中心对称图形:
把一个图形绕着某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫中心对称图形.
5.中心对称作图步骤
① 连结决定已知图形的形状、大小的各关键点与对称中心,并且延长至2倍,得到各点的对称点.
② 按原图形的连结方式顺次连结对称点即得所作图形.
【要点诠释】
图形变换与图案设计的基本步骤
①确定图案的设计主题及要求;
②分析设计图案所给定的基本图案;
③利用平移、旋转、轴对称对基本图案进行变换,实现由基本图案到各部分图案的有机组合;
④对图案进行修饰,完成图案.
【典型例题】
类型一、平移变换
1.如图1,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图2,则阴影部分的周长为____________.
【思路点拨】
根据两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,得出线段之间的相等关系,进而得出OM+MN+NR+GR+EG+OE=A′D′+CD=1+1=2,即可得出答案.
【答案与解析】
∵两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B′D′的位置,
∴A′M=A′N=MN,MO=DM=DO,OD′=D′E=OE,EG=EC=GC,B′G=RG=RB′,
∴OM+MN+NR+GR+EG+OE=A′D′+CD=1+1=2;
【总结升华】
此题主要考查了平移的性质以及等边三角形的性质,根据题意得出A′M=A′N=MN,MO=DM=DO,
OD′=D′E=OE,EG=EC=GC,B′G=RG=RB′是解决问题的关键.
举一反三:
【变式】(2015•顺义区一模)如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.
(1)画出△DEC平移后的三角形;
(2)若BC=,BD=6,CE=3,求AG的长.
【答案】解:(1)△AGB为△DEC平移后的三角形,如下图所示;
(2)∵△AGB为△DEC平移后的三角形,
∴BG=CE=3,BG∥CE,
∵CE⊥BD,
∴BG⊥BD.
在Rt△BDG中,∵∠GBD=90°,BG=3,BD=6,
∴DG==3,
∵四边形ABCD是平行四边形,
∴AD=BC=2,
∴AG=DG﹣AD=3﹣2=.
2.如图(1),已知的面积为3,且现将沿CA方向平移CA长度得到.
(1)求所扫过的图形面积;
(2)试判断,AF与BE的位置关系,并说明理由;
(3)若求AC的长.
B
C
A
()
F
E
【思路点拨】(1)根据平移的性质及平行四边形的性质可得到S△EFA=S△BAF=S△ABC,从而便可得到四边形CEFB的面积;
(2)由已知可证得平行四边形EFBA为菱形,根据菱形的对角线互相垂直平分可得到AF与BE的位置关系为垂直;
(3)作BD⊥AC于D,结合三角形的面积求解.
【答案与解析】(1)由平移的性质得
AF∥BC,且AF=BC,△EFA≌△ABC
∴四边形AFBC为平行四边形
S△EFA=S△BAF=S△ABC=3
∴四边形EFBC的面积为9;
(2)BE⊥AF
证明:由(1)知四边形AFBC为平行四边形
∴BF∥AC,且BF=AC
又∵AE=CA
∴BF∥AE且BF=AE
∴四边形EFBA为平行四边形又已知AB=AC
∴AB=AE
∴平行四边形EFBA为菱形
∴BE⊥AF;
(3)如上图,作BD⊥AC于D
∵∠BEC=15°,AE=AB
∴∠EBA=∠BEC=15°
∴∠BAC=2∠BEC=30°
∴在Rt△BAD中,AB=2BD
设BD=x,则AC=AB=2x
∵S△ABC=3,且S△ABC=AC•BD=•2x•x=x2
∴x2=3
∵x为正数
∴x=
∴AC=2.
【总结升华】此题主要考查了全等三角形的判定,平移的性质,菱形的性质等知识点的综合运用及推理计算能力.
类型二、轴对称变换
3(2016•贵阳模拟)(1)数学课上,老师出了一道题,如图①,Rt△ABC中,∠C=90°,,求证:∠B=30°,请你完成证明过程.
(2)如图②,四边形ABCD是一张边长为2的正方形纸片,E、F分别为AB、CD的中点,沿过点D的抓痕将纸片翻折,使点A落在EF上的点A′处,折痕交AE于点G,请运用(1)中的结论求∠ADG的度数和AG的长.
(3)若矩形纸片ABCD按如图③所示的方式折叠,B、D两点恰好重合于一点O(如图④),当AB=6,求EF的长.
【思路点拨】(1)Rt△ABC中,根据sinB═=,即可证明∠B=30°;
(2)求出∠FA′D的度数,利用翻折变换的性质可求出∠ADG的度数,在Rt△A'FD中求出A'F,得出A'E,在Rt△A'EG中可求出A'G,利用翻折变换的性质可得出AG的长度.
(3)先判断出AD=AC,得出∠ACD=30°,∠DAC=60°,从而求出AD的长度,根据翻折变换的性质可得出∠DAF=∠FAO=30°,在Rt△ADF中求出DF,继而得出FO,同理可求出EO,再由EF=EO+FO,即可得出答案.
【答案与解析】
(1)证明:Rt△ABC中,∠C=90°,,
∵sinB==,
∴∠B=30°;
(2)解:∵正方形边长为2,E、F为AB、CD的中点,
∴EA=FD=×边长=1,
∵沿过点D的抓痕将纸片翻折,使点A落在EF上的点A′处,
∴A′D=AD=2,
∴=,
∴∠FA′D=30°,
可得∠FDA′=90°﹣30°=60°,
∵A沿GD折叠落在A′处,
∴∠ADG=∠A′DG,AG=A′G,
∴∠ADG===15°,
∵A′D=2,FD=1,
∴A′F==,
∴EA′=EF﹣A′F=2﹣,
∵∠EA′G+∠DA′F=180°﹣∠GA′D=90°,
∴∠EA′G=90°﹣∠DA′F=90°﹣30°=60°,
∴∠EGA′=90°﹣∠EA′G=90°﹣60°=30°,
则A′G=AG=2EA′=2(2﹣);
(3)解:∵折叠后B、D两点恰好重合于一点O,
∴AO=AD=CB=CO,
∴DA=,
∵∠D=90°,
∴∠DCA=30°,
∵AB=CD=6,
在Rt△ACD中,=tan30°,
则AD=DC•tan30°=6×=2,
∵∠DAF=∠FAO=∠DAO==30°,
∴=tan30°=,
∴DF=AD=2,
∴DF=FO=2,
同理EO=2,
∴EF=EO+FO=4.
【总结升华】本题考查了翻折变换的知识,涉及了含30°角的直角三角形的性质、平行四边形的性质,综合考察的知识点较多,注意将所学知识融会贯通.
举一反三:
【变式】(2016·松北区模拟)如图(1)是四边形纸片ABCD,其中∠B=120°,∠D=50°.若将其右下角向内这出△PCR,恰使CP∥AB,RC∥AD,如图(2)所示,则∠C= 度.
【答案】∵∠CPR=∠B=×120°=60°,∠CRP=∠D=×50°=25°,
∴∠C=180°-60°-25°=95°.
4. 如图1,矩形纸片ABCD的边长分别为a,b(a
(2)若∠QPC的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕PQ,MN间的距离有何变化?请说明理由.
(3)若∠QPC的角度在每次翻折的过程中都为45°(如图4),每次翻折后,非重叠部分的四边形MC′QD,及四边形BPA′N的周长与a,b有何关系,为什么?
(1) (2) (3) (4)
【思路点拨】(1)猜想两直线平行,由矩形的对边平行,得到一组内错角相等,翻折前后对应角相等,那么可得到PQ与MN被MP所截得的内错角相等,得到平行.
(2)作出两直线间的距离.∵PM长相等,∠NPM是不变的,所以利用相应的三角函数可得到两直线间的距离不变.
(3)由特殊角得到所求四边形的形状,把与周长相关的边转移到同一线段求解.
【答案与解析】
(1)PQ∥MN.
∵四边形ABCD是矩形,∴AD∥BC,且M在AD直线上,则有AM∥BC.
∴∠AMP=∠MPC.
由翻折可得:∠MPQ=∠CPQ=∠MPC,
∠NMP=∠AMN=∠AMP,
∴∠MPQ=∠NMP,故PQ∥MN.
(2)两折痕PQ,MN间的距离不变.
过P作PH⊥MN,则PH=PM•sin∠PMH,
∵∠QPC的角度不变,
∴∠C′PC的角度也不变,则所有的PM都是平行的.
又∵AD∥BC,
∴所有的PM都是相等的.
又∵∠PMH=∠QPC,故PH的长不变.
(3)当∠QPC=45°时,
四边形PCQC′是正方形,
四边形C′QDM是矩形.
∵C′Q=CQ,C′Q+QD=a,
∴矩形C′QDM的周长为2a.
同理可得矩形BPA′N的周长为2a,∴两个四边形的周长都为2a,与b无关.
【总结升华】翻折前后对应角相等,对应边相等,应注意使用相应的三角函数,平行线的判断,特殊四边形的判定.
类型三、旋转变换
【高清课堂 图形的变换 例4】
5.已知O是等边三角形ABC内一点,∠AOB=110°,∠BOC=135°,试问:
(1)以OA,OB,OC为边能否构成一个三角形?若能,求出该三角形各角的度数;若不能,请说明理由;
(2)如果∠AOB的大小保持不变,那么当∠BOC等于多少度时,以OA,OB,OC为边的三角形是一个直角三角形?
【思路点拨】因为△ABC是等边三角形,所以可以运用旋转将△BCO转至△ACD.
【答案与解析】(1)以OC为边作等边△OCD,连AD.
∵ △ABC是等边三角形
∴ ∠BCO=∠ACD (∠BCO+∠ACO=60°,∠ACD+∠ACO=60°)
∵ BC=AC,OC=CD
∴ △BCO≌△ACD (SAS)
∴ OB=AD,∠ADC=∠BOC
又∵OC=OD
∴△OAD是以线段OA,OB,OC为边构成的三角形
∵ ∠AOB=110°, ∠BOC=135°
∴ ∠AOC=115°
∴ ∠AOD=115°-60°=55°
∵ ∠ADC=135°
∴ ∠ADO=135°-60°=75°
∴ ∠OAD=180°-55°-75°=50°
∴ 以线段OA,OB,OC为边构成的三角形的各角是50°、55°、75°.
(2)∠AOB+∠AOC+∠BOC=∠AOB+∠AOC+∠ADC
=∠AOB+(∠AOD+∠DOC)+(∠ADO+∠CDO)
=∠110°+(∠AOD+60°)+(∠ADO+60°) =360°
∴∠AOD+∠ADO=130°
∴∠OAD=50°
当∠AOD是直角时,∠AOD=90°,∠AOC=90°+60°=150°,∠BOC=100°;
当∠ADO是直角时,∠ADC=90°+60°=150°,∠BOC=150°.
【总结升华】此题主要运用旋转的性质、等边三角形的判定、勾股定理的逆定理等知识,渗透分类讨
论思想.
6 . 如图1,O为正方形ABCD的中心,分别延长OA、OD到点F、E,使OF=2OA,OE=2OD,连接
EF.将△EOF绕点O逆时针旋转角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当=30°时,求证:△AOE1为直角三角形.
【思路点拨】(1)要证AE1=BF1,就要首先考虑它们是全等三角形的对应边;
(2)要证△AOE1为直角三角形,就要考虑证∠E1AO=90°.
【答案与解析】(1)AE1=BF1,证明如下:
∵O为正方形ABCD的中心,∴OA=OB=OD.∴OE=OF .
∵△E1OF1是△EOF绕点O逆时针旋转角得到,∴OE1=OF1.
∵ ∠AOB=∠EOF=900, ∴ ∠E1OA=900-∠F1OA=∠F1OB.
在△E1OA和△F1OB中,,∴△E1OA≌△F1OB(SAS).
∴ AE1=BF1.
(2)取OE1中点G,连接AG.
∵∠AOD=900,=30° ,
∴ ∠E1OA=900-=60°.
∵OE1=2OA,∴OA=OG,∴ ∠E1OA=∠AGO=∠OAG=60°.
∴ AG=GE1,∴∠GAE1=∠GE1A=30°.
∴ ∠E1AO=90°.
∴△AOE1为直角三角形.
【总结升华】正方形的性质,旋转的性质,全等三角形的判定和性质,直角三角形的判定.
举一反三:
【变式】如图,P为正方形ABCD内一点,若PA=a,PB=2a,PC=3a(a>0).
(1)求∠APB的度数;
(2)求正方形ABCD的面积.
【答案】(1)将△ABP绕点B顺时针方向旋转90°得△CBQ.
则△ABP≌△CBQ且PB⊥QB.
于是PB=QB=2a,.
在△PQC中,∵ ,.
∴ .
∴ .
∵ △PBQ是等腰直角三角形,
∴ ∠BPQ=∠BQP=45°.
故∠APB=∠CQB=90°+45°=135°.
(2)∵ ∠APQ=∠APB+∠BPQ=135°+45°=180°,
∴ 三点A、P、Q在同一直线上.
在Rt△AQC中,.
∴ 正方形ABCD的面积.
专题5.1 图形的变换-平移、轴对称、旋转(知识讲解)-2022年中考数学基础知识专项讲练(全国通用): 这是一份专题5.1 图形的变换-平移、轴对称、旋转(知识讲解)-2022年中考数学基础知识专项讲练(全国通用),共18页。
01中考总复习:实数--知识讲解(基础): 这是一份01中考总复习:实数--知识讲解(基础),共8页。
(人教版)数学中考总复习45中考总复习:图形的变换(基础)珍藏版: 这是一份(人教版)数学中考总复习45中考总复习:图形的变换(基础)珍藏版,文件包含中考总复习图形的变化--巩固练习基础doc、中考总复习图形的变换--知识讲解基础doc等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。