中考总复习：特殊三角形--知识讲解（基础）

这是一份中考总复习：特殊三角形--知识讲解（基础），共14页。

【考纲要求】
【高清课堂：等腰三角形与直角三角形 考纲要求】
1.了解等腰三角形、等边三角形、直角三角形的概念，会识别这三种图形；理解等腰三角形、等边三角形、直角三角形的性质和判定；
2.能用等腰三角形、等边三角形、直角三角形的性质和判定解决简单问题；
3.会运用等腰三角形、等边三角形、直角三角形的知识解决有关问题．
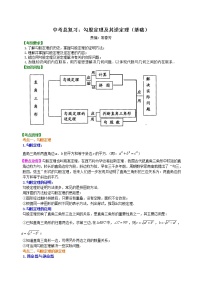
【知识网络】
【考点梳理】
考点一、等腰三角形
1.等腰三角形：有两条边相等的三角形叫做等腰三角形.
2.性质：
(1)具有三角形的一切性质.
(2)两底角相等(等边对等角)
(3)顶角的平分线，底边中线，底边上的高互相重合(三线合一)
(4)等边三角形的各角都相等，且都等于60°.
3.判定：
(1)如果一个三角形有两个角相等，那么这两个角所对的边也相等(等角对等边)；
(2)三个角都相等的三角形是等边三角形；
(3)有一个角为60°的等腰三角形是等边三角形.
要点诠释：
(1)腰、底、顶角、底角是等腰三角形特有的概念；
(2)等边三角形是特殊的等腰三角形.
考点二、直角三角形
1.直角三角形：有一个角是直角的三角形叫做直角三角形.
2性质：
(1)直角三角形中两锐角互余.
(2)直角三角形中，30°锐角所对的直角边等于斜边的一半.
(3)在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°.
(4)勾股定理：直角三角形中，两条直角边的平方和等于斜边的平方.
(5)勾股定理逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形.
(6)直角三角形中，斜边上的中线等于斜边的一半.
3．判定：
(1)有两内角互余的三角形是直角三角形.
(2)一条边上的中线等于该边的一半，则这条边所对的角是直角，这个三角形是直角三角形.
(3)如果三角形两边的平方和等于第三边的平方，则这个三角形是直角三角形，第三边为斜边.
【典型例题】
类型一、等腰三角形
1．如图，等腰三角形一腰上的高与底边所成的角等于( )
A.顶角的2倍 B.顶角的一半 C.顶角 D.底角的一半

【思路点拨】等角的余角相等.
【答案】B.
【解析】如图，△ABC中，AB=AC，BD⊥AC于D，所以∠ABC=∠C，∠BDC=90°，所以∠DBC=90°-∠C=
90°-(180-∠A)= ∠A，
【总结升华】本题适用于任何一种等腰三角形,可以试着证明在钝角三角形中结论一样成立；总结规律，等腰三角形一腰上的高与底边所成的角等于顶角的一半.
举一反三：
【变式】如图，在△ABC中，AB＝AC，∠A＝36°，BD、CE分别是△ABC、△BCD的角平分线，则图中的等腰三角形有（ ）A．5个 B．4个 C．3个 D．2个
【答案】A．
2．（2015秋•南通校级月考）如图，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=30cm，DE=2cm，则BC= cm．
【思路点拨】作出辅助线后根据等腰三角形的性质得出BE=30，DE=2，进而得出△BEM为等边三角形，△EFD为等边三角形，从而得出BN的长，进而求出答案．
【答案】32;
【解析】
解：延长ED交BC于M，延长AD交BC于N，作DF∥BC，
∵AB=AC，AD平分∠BAC，
∴AN⊥BC，BN=CN，
∵∠EBC=∠E=60°，
∴△BEM为等边三角形，
∴△EFD为等边三角形，
∵BE=30，DE=2，
∴DM=28，
∵△BEM为等边三角形，
∴∠EMB=60°，
∵AN⊥BC，
∴∠DNM=90°，
∴∠NDM=30°，
∴NM=14，
∴BN=16，
∴BC=2BN=32，
故答案为32．
【总结升华】本题主要考查了等腰三角形的性质和等边三角形的性质，能求出MN的长是解决问题的关键．
类型二、直角三角形
3．将一张矩形纸片如图所示折叠，使顶点落在点.已知，，则折痕的长为( )
A. B. C. D.

【思路点拨】直角三角形是常见的几何图形，在习题中比较多的利用数形结合解决相应的问题.常用的是两锐角互余，三边满足勾股定理和直角三角形中，30°角所对的边等于斜边的一半.
【答案】C.
【解析】由折叠可知，∠CED=∠C′ED =30°，因为在矩形ABCD中，∠C等于90°，CD=AB=2，
所以在Rt△DCE中，DE=2CD=4.故选C.
【总结升华】折叠题型一定要注意对应的边相等，对应的角相等.
【变式】 如图，一张直角三角形纸片，两直角边AC=4cm，BC=8cm，将△ABC折叠，点B与点A重合，折痕为DE，则DE的长为( )．
A. B. C. D.5

【答案】B.
解析：由折叠可知，AD=BD，DE⊥AB， ∴BE=AB
设BD为x，则CD=8-x
∵∠C=90°，AC=4，BC=8，∴AC2+BC2=AB2
∴AB2=42+82=80，∴AB=，∴BE=
在Rt△ACD中，AC2+CD2=AD2 ，∴42+(8-x)2=x2，解得x=5
在Rt△BDE中，BE2+DE2=BD2，即()2+DE2=52，∴DE=， 故选B.
4．已知：在直角△ABC中，∠C=90°，BD平分∠ABC且交AC于D.
(1)若∠BAC=30°，求证: AD=BD；
(2)若AP平分∠BAC且交BD于P，求∠BPA的度数.

图1 图2
【思路点拨】(1)利用直角三角形两锐角互余，求得∠ABD=∠A=30°，得出AD=BD.
(2)利用三角形内角和及角平分线定义或利用三角形外角性质.
【答案与解析】
(1)证明：∵∠BAC=30°，∠C=90°，∴∠ABC=60°
又∵ BD平分∠ABC， ∴∠ABD=30°，∴ ∠BAC =∠ABD，∴BD=AD；
(2)解法一： ∵∠C=90°，∴∠BAC+∠ABC=90°
∴=45°
∵ BD平分∠ABC，AP平分∠BAC
∠BAP=，∠ABP=
即∠BAP+∠ABP=45°
∴∠APB=180°-45°=135°
解法二： ∵∠C=90°，∴∠BAC+∠ABC=90°
∴=45°
∵BD平分∠ABC，AP平分∠BAC
∠DBC=，∠PAC=
∴∠DBC+∠PAD=45°
∴∠APB=∠PDA+∠PAD =∠DBC+∠C+∠PAD=∠DBC+∠PAD+∠C=45°+90°=135°.
【总结升华】本题利用了：1、直角三角形的性质，两锐角互余，2、角的平分线的性质，3、三角形的外角与内角的关系．
类型三、综合运用
5 . 已知ABC的两边AB、AC的长是关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0的两个实数根，第三边BC的长为5.
（1）k为何值时，ΔABC是以BC为斜边的直角三角形？
（2）k为何值时，ΔABC是等腰三角形？并求出ΔABC的周长。
【思路点拨】△ABC的两边的长是关于x的一元二次方程的两个实数根，应该想到一元二次方程中根与系数的关系.
【答案与解析】(1)∵AB、ACAB、AC的长是关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0的两个实数根,
∴AB+AC=2k+3,AB×AC= k2+3k+2
又∵ΔABC是以BC为斜边的直角三角形，BC=5
∴
∴
即
∴
当k=-5时，方程为
解得（不合题意，舍去）
当k=2时，方程为
解得
∴当k=2时，ΔABC是以BC为斜边的直角三角形.
(2)当ΔABC是等腰三角形时，则有①AB=AC,②AB=BC,③AB=BC三种情况：
∵△==1>0
∴AB≠AC,故第一种情况不成立；
当AB=BC或AC=BC时，5是方程x2-(2k+3)x+k2+3k+2=0的根
∴
当k=3时，，
∴
∴等腰三角形的边长分别是5,5,4.周长为14；
当k=4时，，
∴
所以等腰三角形的边长是5,5,6，周长是16.
【总结升华】当三角形是等腰三角形并且未明确哪两边为腰时,要注意分类讨论.
【变式】已知等腰三角形三边的长为a、b、c且a=c，若关于x的一元二次方程ax2-bx+c=0的两根之差为，则等腰三角形的一个底角是（ ）.
A. 150 B. 300 C. 450 D. 600
【答案】B.
6．（2015春•威海期末）如图，△ABC中，∠BAC=90°，AB=AC，AD⊥BC，垂足是D，AE平分∠BAD，交BC于点E，EH⊥AB，垂足是H．在AB上取一点M，使BM=2DE，连接ME．求证：ME⊥BC．
【思路点拨】根据EH⊥AB于H，得到△BEH是等腰直角三角形，然后求出HE=BH，再根据角平分线上的点到角的两边距离相等可得DE=HE，然后求出HE=HM，从而得到△HEM是等腰直角三角形，再根据等腰直角三角形的性质求解即可．
【答案与解析】解：∵∠BAC=90°，AB=AC，
∴∠B=∠C=45°，
∵EH⊥AB于H，
∴△BEH是等腰直角三角形，
∴HE=BH，∠BEH=45°，
∵AE平分∠BAD，AD⊥BC，
∴DE=HE，
∴DE=BH=HE，
∵BM=2DE，
∴HE=HM，
∴△HEM是等腰直角三角形，
∴∠MEH=45°，
∴∠BEM=45°+45°=90°，
∴ME⊥BC．
【总结升华】本题考查等腰直角三角形的判定与性质，角平分线上的点到角的两边距离相等的性质，熟记性质并证明出等腰直角三角形是解题的关键．
【高清课堂：等腰三角形与直角三角形 例6】
【变式】如图，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC交AC的延长线于M，连接CD，给出四个结论：①∠ADC=45°；②BD=AE；③AC+CE=AB；④ AB-BC=2MC；其中正确的结论有( ) A.1个 B.2个 C.3个 D.4个
【答案】D.