

苏教版数学六年级上学期期中测试卷5
展开江苏省苏州市张家港市红蕾小学六年级(上)期中数学试卷
一、认真思考,正确填写.(每空1分,共24分)
1.的倒数是 ; 的倒数是1.
2.的是 ; 的是.
3.3﹕4==6÷ =9﹕ .
4.“实际用电量比原计划节约了”是把 看作单位“1”,数量关系式是 ×= .
5.分= 秒
米= 厘米
9.04立方分米= 毫升
4500立方分米= 立方米.
6.不计算,在横线填上“>”、“<”或“=”.
×
÷ .
7.一个正方体的棱长总和是48厘米,它的表面积是 平方厘米,体积是 立方厘米.
8.一种汽车行千米用汽油升,这种汽车行1千米用汽油 升,这种汽车用1升汽油可行 千米.
9.一块橡皮的体积约是6 ;一个纯净水桶的容积大约19 .
10.一项工程,甲队独做10天完成,乙队独做15天完成.甲、乙两队每天完成这项工程量的最简整数比是 ,比值为 .
二、精挑细选(10分,每题2分)
11.至少( )个完全一样的小正方体可以拼成一个稍大的正方体.
A.4 B.8 C.9
12.一个铁桶可装水100升,这个桶的体积可能是( )
A.100立方分米 B.98立方分米 C.105立方分米
13.一个正方体的棱长扩大3倍,体积扩大( )倍.
A.3 B.9 C.27
14.两根都是1米长的钢管,第一根用去米,第二根用去.用去部分比较( )
A.两根用去一样长 B.第一根用去长
C.第二根用去长
15.下面的图形中,折叠后能围成正方体的是( )
A. B. C. D.
三、慎思妙断(10分,每题2分)
16.1米的和7米的一样长. .(判断对错)
17.0.13=0.3 .(判断对错)
18.甲数除以乙数等于甲数乘乙数的倒数. .(判断对错)
19.棱长是6厘米的正方体表面积和体积相等. .(判断对错)
20.一个不为0的数乘积小于这个数. .(判断对错)
四、看清题目,巧思妙算.
21.
直接写得数. 2×= | 1÷= | ﹣= |
÷= | 8÷= | ÷12= |
×0= | ×= | |
22.计算下面各题.
×× | ××15 | 4×÷ | ÷÷ |
23.解方程.
x=
x=.
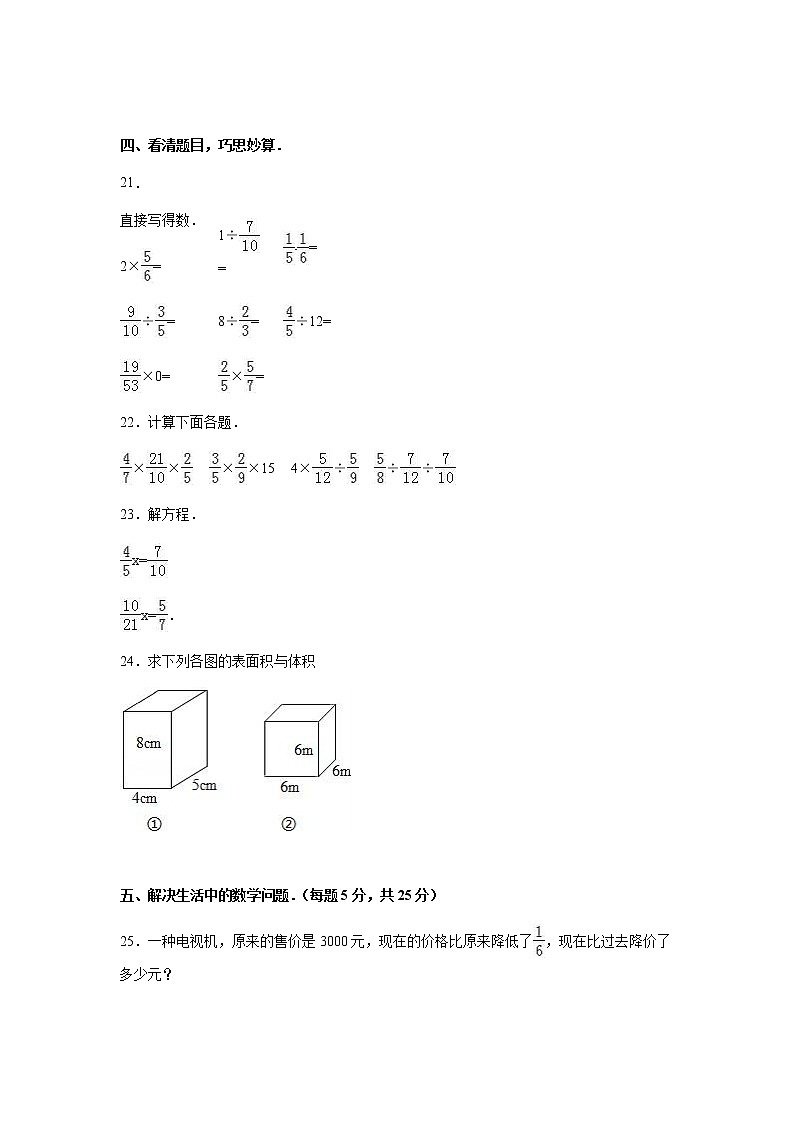
24.求下列各图的表面积与体积
五、解决生活中的数学问题.(每题5分,共25分)
25.一种电视机,原来的售价是3000元,现在的价格比原来降低了,现在比过去降价了多少元?
26.商店运来一批水果,其中有60筐苹果,占运来水果筐数的,这批水果共有多少筐?(用方程解)
27.水果店运来梨、苹果、香蕉共120千克,梨、苹果和香蕉的质量比是3:7:2,运来的梨、苹果和香蕉各多少千克?
28.小明家客厅的形状是一个长方体,长8米,宽4米,高3米.要在客厅四周的墙上贴墙纸(门窗面积为14平方米),至少要用墙纸多少平方米?
29.永新面粉厂小时可以磨面粉吨.照这样计算,小时可以磨面粉多少吨??
江苏省苏州市张家港市红蕾小学六年级(上)期中数学试卷
参考答案与试题解析
一、认真思考,正确填写.(每空1分,共24分)
1.的倒数是 ; 1 的倒数是1.
【考点】倒数的认识.
【分析】直接根据倒数的定义进行解答即可,注意1的倒数是它本身.
【解答】解:的倒数是;
1的倒数是1.
故答案为:;1.
2.的是 ; 的是.
【考点】分数乘法;分数除法.
【分析】求的是多少,根据分数乘法的意义,用乘法计算;已知一个数的是,求这个数,根据分数除法的意义,用除法计算.
【解答】解:×=;
=.
故答案为:,.
3.3﹕4==6÷ 8 =9﹕ 12 .
【考点】比与分数、除法的关系.
【分析】根据比的基本性质3:4的前、后项都乘3就是9:12;根据比与分数的关系3:4=,再根据分数的基本性质分子、分母都乘4就是;根据比与除法的关系3:4=3÷4,再根据商不变的性质被除数、除数都乘2就是6÷8.
【解答】解:3:4==6÷8=9:12.
故答案为:16,8,12.
4.“实际用电量比原计划节约了”是把 计划用电量 看作单位“1”,数量关系式是 计划用电量 ×= 节约的电量 .
【考点】单位“1”的认识及确定.
【分析】根据判断单位“1”的方法:一般是在比、占、是、相当于后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”据此解答即可.
【解答】解:实际用电量比计划节约,这里是把“计划用电量”看作单位“1”,数量关系式是计划用电量×=节约的电量.
故答案为:计划用电量、节约的电量.
5.分= 35 秒
米= 40 厘米
9.04立方分米= 9040 毫升
4500立方分米= 4.5 立方米.
【考点】时、分、秒及其关系、单位换算与计算;长度的单位换算;体积、容积进率及单位换算.
【分析】把分换算成秒数,用乘进率60即可;
把米换算为厘米数,用乘进率100;
把9.04立方分米数换算成毫升数,用9.04乘进率1000;
把4500立方分米换算为立方米数,用4500除以进率1000.
【解答】解:分=35秒
米=40厘米
9.04立方分米=9040毫升
4500立方分米=4.5立方米;
故答案为:35,40,9040,4.5.
6.不计算,在横线填上“>”、“<”或“=”.
× >
÷ < .
【考点】积的变化规律;商的变化规律.
【分析】一个数(0除外)乘大于1的数,积大于这个数;一个数(0除外)除以大于1的数,积小于这个数;据此解答.
【解答】解:×>
÷<.
故答案为:>,<.
7.一个正方体的棱长总和是48厘米,它的表面积是 96 平方厘米,体积是 64 立方厘米.
【考点】长方体和正方体的表面积;长方体和正方体的体积.
【分析】由正方体的特征可知:正方体有12 条棱长,且每条棱长都相等,于是可以求出正方体的棱长的长度,进而可以求出这个正方体的表面积和体积.
【解答】解:48÷12=4厘米
4×4×6=96平方厘米
4×4×4=64立方厘米
答:它的表面积是96平方厘米,体积是64立方厘米.
故答案为:96;64.
8.一种汽车行千米用汽油升,这种汽车行1千米用汽油 升,这种汽车用1升汽油可行 千米.
【考点】分数除法.
【分析】根据题意,要求这种汽车行1千米用汽油多少升,用汽油升除以行驶的千米;要求这种汽车用1升汽油可行多少千米,用行千米除以使用汽油升即可.
【解答】解:根据题意可得:
÷=(升);
÷=(千米).
答:这种汽车行1千米用汽油升,这种汽车用1升汽油可行千米.
故答案为:,.
9.一块橡皮的体积约是6 立方厘米 ;一个纯净水桶的容积大约19 升 .
【考点】根据情景选择合适的计量单位.
【分析】根据生活经验、对体积单位、容积单位和数据大小的认识,可知:一块橡皮的体积约是6 立方厘米;一个纯净水桶的容积大约19 升;据此解答.
【解答】解:一块橡皮的体积约是6 立方厘米;一个纯净水桶的容积大约19 升;
故答案为:立方厘米,升.
10.一项工程,甲队独做10天完成,乙队独做15天完成.甲、乙两队每天完成这项工程量的最简整数比是 3:2 ,比值为 .
【考点】比的意义;简单的工程问题.
【分析】把工作总量看作单位“1”,根据“工作总量÷工作时间=工作效率”分别求出甲队和乙队的工作效率,进而根据题意,进行比即可.
【解答】解:(1÷10):(1÷15),
=:,
=(×30):(×30),
=3:2;
(1÷10):(1÷15),
=:,
=÷,
=;
故答案为:3:2、.
二、精挑细选(10分,每题2分)
11.至少( )个完全一样的小正方体可以拼成一个稍大的正方体.
A.4 B.8 C.9
【考点】正方体的特征.
【分析】假设小正方体的棱长是1厘米,体积是1立方厘米,拼成的稍大的正方体棱长至少是2厘米,体积为8立方厘米,进一步求出个数.
【解答】解:假设小正方体的棱长是1厘米,体积:1×1×1=1(立方厘米);
稍大的正方体棱长至少是2厘米,体积:2×2×2=8(立方厘米);
需要小正方体的个数:8÷1=8(个).
故选:B.
12.一个铁桶可装水100升,这个桶的体积可能是( )
A.100立方分米 B.98立方分米 C.105立方分米
【考点】体积、容积进率及单位换算.
【分析】一个铁桶可装水100升,指的是铁桶的容积,计算容积,要从容器的里面量需要的数据;而物体的体积是指物体所占空间的大小,计算体积,要从容器的外面量需要的数据,故体积大于容积.
【解答】解:计算容积,要从容器的里面量需要的数据,
计算体积,要从容器的外面量需要的数据,故体积大于容积.
故选:C.
13.一个正方体的棱长扩大3倍,体积扩大( )倍.
A.3 B.9 C.27
【考点】长方体和正方体的体积.
【分析】正方体的体积等于棱长的立方,它的棱长扩大几倍,则它的体积扩大棱长扩大倍数的立方倍,据此规律可得.
【解答】解:正方体的棱长扩大3倍,它的体积则扩大33=27倍.
故选:C.
14.两根都是1米长的钢管,第一根用去米,第二根用去.用去部分比较( )
A.两根用去一样长 B.第一根用去长
C.第二根用去长
【考点】分数的意义、读写及分类;分数大小的比较.
【分析】本题要先求出第二根的是多少米再进行比较,1米的是1×=(米),所以两根用去的一样多.
【解答】解:1×=(米);
所以两根用去的一样多.
故选:A.
15.下面的图形中,折叠后能围成正方体的是( )
A. B. C. D.
【考点】正方体的展开图.
【分析】由平面图形的折叠及正方体的展开图解题.注意只要有“田”字格的展开图都不是正方体的表面展开图.
【解答】解:A可以折叠成一个正方体,符合题意,
B只要有“田”字格的展开图都不是正方体的表面展开图所以它折叠不成正方体,不符合题意,
C围成几何体时,多了一个底面,少了一个侧面,所以不能围成正方体,不符合题意,
D围成几何体时,有两个面重合,故不能围成正方体,不符合题意.
故选:A.
三、慎思妙断(10分,每题2分)
16.1米的和7米的一样长. √ .(判断对错)
【考点】分数大小的比较;分数乘法.
【分析】首先区分和的区别:1米的单位1是1米,7米的单位1是7米,由此进行列式,比较结果解答即可.
【解答】解:1×=(米);
7×=(米);
所以一样长;
故填:√.
17.0.13=0.3 × .(判断对错)
【考点】有理数的乘方.
【分析】可从意义上进行判断:0.3表示3个0.1相加的和;0.13表示3个0.1相乘的积.
【解答】解:0.13表示3个0.1相乘的积;
0.3表示3个0.1相加的和;
故答案为:×.
18.甲数除以乙数等于甲数乘乙数的倒数. × .(判断对错)
【考点】分数除法.
【分析】根据分数除法的计算法则,甲数除以乙数(0除外),等于甲数乘乙数的倒数.据此判断.
【解答】解:因为除数不能为0,所以甲数除以乙数,等于甲数乘乙数的倒数.这种说法是错误的.
故答案为:×.
19.棱长是6厘米的正方体表面积和体积相等. × .(判断对错)
【考点】长方体和正方体的表面积;长方体和正方体的体积.
【分析】正方体的表面积和体积单位不相同,没法比较它们的大小,由此就解决即可.
【解答】解:因为正方体的表面积和体积单位不相同,没法比较它们的大小,
所以原题说法是错误的.
故答案为:×.
20.一个不为0的数乘积小于这个数. √ .(判断对错)
【考点】分数乘法;分数大小的比较.
【分析】根据一个不等于0的数乘一个大于(小于)1的数与原数的关系,即可判断.
【解答】解:根据一个不等于0的数乘一个小于1的数,则积小于第一个数,
所以题目中的说法是正确的;
故答案为:√.
四、看清题目,巧思妙算.
21.
直接写得数. 2×= | 1÷= | ﹣= |
÷= | 8÷= | ÷12= |
×0= | ×= | |
【考点】分数乘法;分数除法.
【分析】根据分数减法、乘法、除法的计算法则,直接进行口算.
【解答】解:
2×= | 1÷= | ﹣= |
÷= | 8÷=12 | ÷12= |
×0=0 | ×=. | |
22.计算下面各题.
×× | ××15 | 4×÷ | ÷÷ |
【考点】分数的四则混合运算.
【分析】(1)按照从左向右的顺序进行计算;
(2)根据乘法交换律进行简算;
(3)按照从左向右的顺序进行计算;
(4)按照从左向右的顺序进行计算.
【解答】解:(1)××
=×
=;
(2)××15
=×15×
=9×
=2;
(3)4×÷
=÷
=3;
(4)÷÷
=÷
=.
23.解方程.
x=
x=.
【考点】方程的解和解方程.
【分析】(1)根据等式的性质,两边同除以即可;
(2)根据等式的性质,两边同除以即可.
【解答】解:(1)x=
x÷=÷
x=;
(2)x=
x=1.5.
24.求下列各图的表面积与体积
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【分析】长方体的表面积S=(ab+bh+ah)×2,体积V=abh;正方体的表面积S=6a2,体积V=a3,长方体的长、宽、高和正方体的棱长都已知,将数据分别代入公式即可求解.
【解答】解:(4×5+4×8+5×8)×2
=(20+32+40)×2
=92×2
=184(平方厘米);
4×5×8=160(立方厘米);
答:这个长方体的表面积是184平方厘米,体积是160立方厘米.
6×6×6=216(平方米);
6×6×6=216(立方米);
答:这个正方体的表面积是216平方米,体积是216立方米.
五、解决生活中的数学问题.(每题5分,共25分)
25.一种电视机,原来的售价是3000元,现在的价格比原来降低了,现在比过去降价了多少元?
【考点】分数乘法应用题.
【分析】把原价看作单位“1”,根据一个数乘分数的意义,用乘法即可求出现在比过去降价了多少元,据此解答.
【解答】解:3000×=500(元),
答:现在比过去降价了500元.
26.商店运来一批水果,其中有60筐苹果,占运来水果筐数的,这批水果共有多少筐?(用方程解)
【考点】分数除法应用题.
【分析】把运来的水果的总筐数看成单位“1”,它的就是苹果的筐数,所以水果的筐数×=苹果的筐数,设出水果的总筐数,根据这个等量关系列出方程求解即可.
【解答】解:设这批水果一共有x筐,由题意得
x=60
x÷=60÷
x=96
答:这批水果共有96筐.
27.水果店运来梨、苹果、香蕉共120千克,梨、苹果和香蕉的质量比是3:7:2,运来的梨、苹果和香蕉各多少千克?
【考点】按比例分配应用题.
【分析】本题可先通过它们的质量比求出它们各占总质量的几分之几,然后按求一个数的几分之几是多少的方法,用乘法求出各有多少千克.据此解答.
【解答】解:120×=30(千克)
120×=70(千克)
120×=20(千克)
答:运来梨30千克,运来苹果70千克,运来香蕉20千克.
28.小明家客厅的形状是一个长方体,长8米,宽4米,高3米.要在客厅四周的墙上贴墙纸(门窗面积为14平方米),至少要用墙纸多少平方米?
【考点】长方体、正方体表面积与体积计算的应用.
【分析】根据题意,要在客厅四周的墙上贴墙纸,求出四面墙壁的面积减去门窗面积即可.
【解答】解:(8×3+4×3)×2﹣14,
=(24+12)×2﹣14,
=36×2﹣14,
=72﹣14,
=58(平方米);
答:至少要用墙纸58平方米.
29.永新面粉厂小时可以磨面粉吨.照这样计算,小时可以磨面粉多少吨??
【考点】分数四则复合应用题.
【分析】小时可以磨面粉吨,根据除法的意义可知,一小时可麿面粉吨,根据乘法的意义,小时可以磨面粉×吨.
【解答】解: ×
=×,
=(吨).
答:小时可以磨面粉吨.









