
2020年辽宁省本溪市、抚顺市、辽阳市中考数学试卷
展开
绝密★启用前
2020年辽宁省本溪市、抚顺市、辽阳市中考数学试卷
试卷副标题
考试范围:xxx;考试时间:xxx 分钟;命题人:xxx
题号 | 一 | 二 | 三 | 总分 |
得分 |
|
|
|
|
| 一、 选择题(共10题) |
1. 的倒数是.
A. B. C. D.
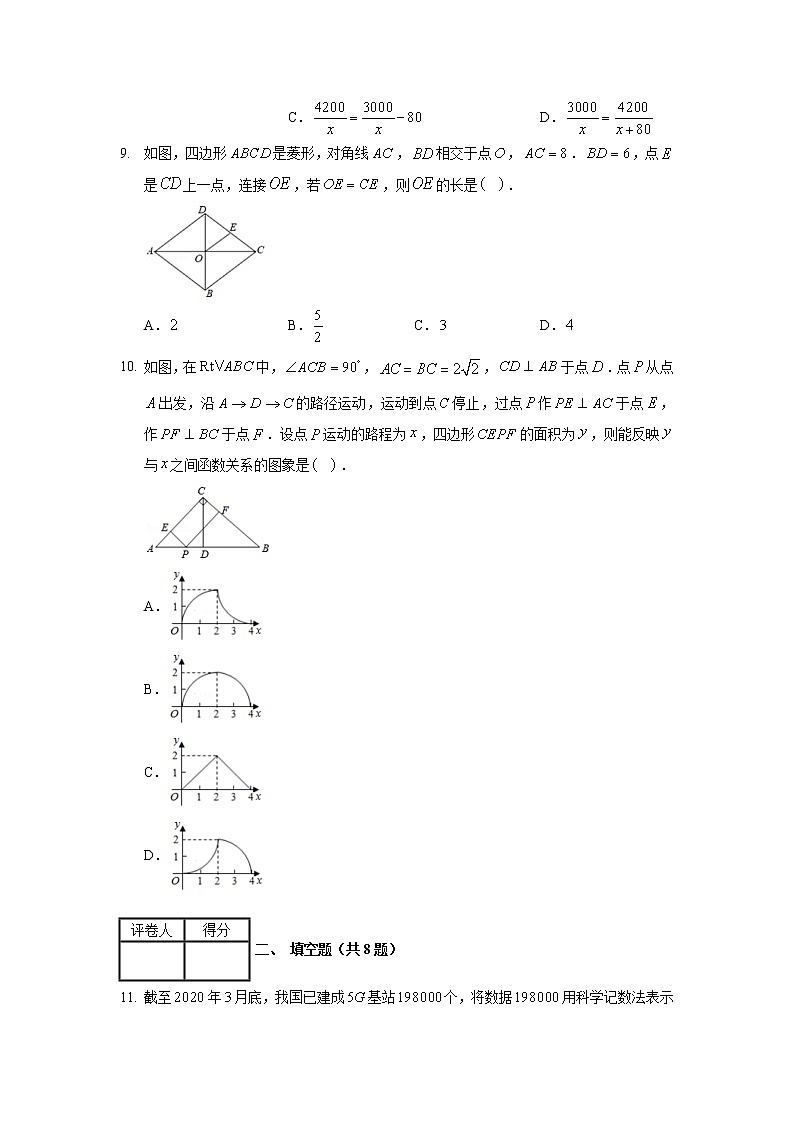
2. 如图是由一个长方体和一个圆锥组成的几何体,它的主视图是.
A.
B.
C.
D.
3. 下列运算正确的是.
A. B.
C. D.
4. 下列图形中,既是轴对称图形又是中心对称图形的是.
A.
B.
C.
D.
5. 某校九年级进行了次数学模拟考试,甲、乙、丙、丁名同学次数学成绩的平均分都是分,方差分别是,,,,则这名同学次数学成绩最稳定的是.
A.甲 B.乙 C.丙 D.丁
6. 一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若,则的度数是.
A. B. C. D.
7. 一组数据,,,,,的中位数是.
A. B. C. D.
8. 随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周件提高到件,平均每人每周比原来多投递件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件件,根据题意可列方程为.
A. B. C. D.
9. 如图,四边形是菱形,对角线,相交于点,.,点是上一点,连接,若,则的长是.
A. B. C. D.
10. 如图,在中,,,于点.点从点出发,沿的路径运动,运动到点停止,过点作于点,作于点.设点运动的路程为,四边形的面积为,则能反映与之间函数关系的图象是.
A.
B.
C.
D.
| 二、 填空题(共8题) |
11. 截至年月底,我国已建成基站个,将数据用科学记数法表示为 .
12. 若一次函数的图象经过点,则 .
13. 若关于的一元二次方程无实数根,则的取值范围是 .
14. 如图是由全等的小正方形组成的图案,假设可以随意在图中取点,那么这个点取在阴影部分的概率是 .
15. 如图,在中,,分别是和的中点,连接,点是的中点,连接并延长,交的延长线于点.若,则的长为 .
16. 如图,在中,,,分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和,作直线,交于点,连接,若,则的长为 .
17. 如图,在中,,点在反比例函数的图象上,点,在轴上,,延长交轴于点,连接,若的面积等于,则的值为 .
18. 如图,四边形是矩形,延长到点,使,连接,点是的中点,连接,,得到 ;点是的中点,连接,,得到;点是的中点,连接,,得到;;按照此规律继续进行下去,若矩形的面积等于,则的面积为 .(用含正整数的式子表示)
| 三、 解答题(共8题) |
19. 先化简,再求值:,其中.
20. 为培养学生的阅读习惯,某中学利用学生课外时间开展了以“走近名著”为主题的读书活动.为了有效了解学生课外阅读情况,现随机调查了部分学生每周课外阅读的时间,设被调查的每名学生每周课外阅读的总时间为小时,将它分为个等级:,, ,,并根据调查结果绘制了如图两幅不完整的统计图:
请你根据统计图的信息,解决下列问题:
(1)本次共调查了 名学生;
(2)在扇形统计图中,等级所对应的扇形的圆心角为 ;
21. 某校计划为教师购买甲、乙两种词典.已知购买本甲种词典和本乙种词典共需元,购买本甲种词典和本乙种词典共需元.
(1)求每本甲种词典和每本乙种词典的价格分别为多少元?
(2)学校计划购买甲种词典和乙种词典共本,总费用不超过元,那么最多可购买甲种词典多少本?
22. 如图,我国某海域有,两个港口,相距海里,港口在港口的东北方向,点处有一艘货船,该货船在港口的北偏西方向,在港口的北偏西方向,求货船与港口之间的距离.(结果保留根号)
23. 超市销售某品牌洗手液,进价为每瓶元.在销售过程中发现,每天销售量(瓶)与每瓶售价(元)之间满足一次函数关系(其中,且为整数),当每瓶洗手液的售价是元时,每天销售量为瓶;当每瓶洗手液的售价是元时,每天销售量为瓶.
(1)求与之间的函数关系式;
(2)设超市销售该品牌洗手液每天销售利润为元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
24. 如图,在平行四边形中,是对角线,,以点为圆心,以的长为半径作,交边于点,交于点,连接.
(1)求证:与相切;
(2)若,,求阴影部分的面积.
25. 如图,射线和射线相交于点,,且.点是射线上的动点(点不与点和点重合),作射线,并在射线上取一点,使,连接,.
(1)如图① ,当点在线段上,时,请直接写出的度数;
(2)如图② ,当点在线段上,时,请写出线段,,之间的数量关系,并说明理由;
(3)当,时,请直接写出的值.
26. 如图,抛物线过点和.点是抛物线的顶点,点是轴下方抛物线上的一点,连接,.
(1)求抛物线的解析式;
(2)如图① ,当时,求点的坐标;
(3)如图② ,在(2)的条件下,抛物线的对称轴交轴于点,交线段于点,点是线段上的动点(点不与点和点重合),连接,将沿折叠,点的对应点为点,与的重叠部分为,在坐标平面内是否存在一点,使以点,,,为顶点的四边形是矩形?若存在,请直接写出点的坐标,若不存在,请说明理由.
参考答案及解析
一、 选择题
1. 【答案】A
【解析】有理数的倒数是.
故选:
【点评】本题考查了倒数,分子分母交换位置是求一个数的倒数的关键.
2. 【答案】C
【解析】从正面看,“底座长方体”看到的图形是矩形,“上部圆锥体”看到的图形是等腰三角形,因此选项的图形符合题意.
故选:
【点评】本题考查简单几何体的三视图的画法,画三视图时要注意“长对正、宽相等、高平齐”.
3. 【答案】B
【解析】.与不是同类项,不能合并,所以错误;
.,所以正确;
.,所以错误;
. ,所以错误.
故选:
【点评】本题主要考查了合并同类项,同底数幂的除法,同底数幂的乘法,幂的乘方等运算,熟练掌握运算法则是解答此题的关键.
4. 【答案】D
【解析】、是轴对称图形,不是中心对称图形,故本选项不合题意;
、既不是轴对称图形,也不是中心对称图形,故本选项不合题意;
、是轴对称图形,不是中心对称图形,故本选项不合题意;
、既是轴对称图形又是中心对称图形,故本选项符合题意.
故选:
【点评】本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转度后两部分重合.
5. 【答案】A
【解析】,,,,且平均数相等,
,
这名同学3次数学成绩最稳定的是甲.
故选:
6. 【答案】C
【解析】,
,
三角形是等腰直角三角形,
.
故选:
【点评】本题考查了等腰直角三角形的性质,平行线的性质,熟练掌握平行线的性质是解题的关键.
7. 【答案】B
【解析】一组数据,,,,,的中位数是.
故选:
【点评】本题主要考查中位数,解题的关键是掌握中位数的定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
8. 【答案】D
【解析】设原来平均每人每周投递快件件,则现在平均每人每周投递快件件,
依题意,得:.
故选:
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
9. 【答案】B
【解析】 菱形的对角线、相交于点,
,,,
由勾股定理得,,
,
,
,
四边形是菱形,
,
,
,
,
是的中位线,
.
故选:
【点评】本题考查了菱形的性质,三角形的中位线平行于第三边并且等于第三边的一半,勾股定理,熟记性质与定理是解题的关键.
10. 【答案】A
【解析】 在中,,,
,,
于点,
,
,,
四边形是矩形,
,,
点运动的路程为,
,
则,
,
四边形的面积为,
当点从点出发,沿路径运动时,
即时,
,
当时,抛物线开口向下;
当点沿路径运动时,
即时,
是的平分线,
,
四边形是正方形,
,,
,
.
当时,抛物线开口向上,
综上所述:能反映与之间函数关系的图象是:.
故选:
【点评】本题考查了动点问题的函数图象,解决本题的关键是掌握二次函数的性质.
二、 填空题
11. 【答案】;
【解析】.
故答案为:
【点评】此题考查科学记数法表示较大的数的方法,准确确定与值是关键.
12. 【答案】;
【解析】 一次函数的图象经过点,
.
故答案为:
【点评】本题考查了一次函数图象上点的坐标特征,牢记直线上任意一点的坐标都满足函数关系式是解题的关键.
13. 【答案】;
【解析】由题意可知:,
.
故答案为:
【点评】本题考查了一元二次方程根的判别式,需要掌握一元二次方程没有实数根相当于判别式小于零.
14. 【答案】;
【解析】设阴影部分的面积是,则整个图形的面积是,
则这个点取在阴影部分的概率是.
故答案为:
【点评】本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件;然后计算阴影区域的面积在总面积中占的比例,这个比例即事件发生的概率.
15. 【答案】;
【解析】 ,分别是和的中点,
是的中位线,
,,
,,
点是的中点,
,
,
.
故答案为:
【点评】本题主要考查了三角形中位线定理以及全等三角形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
16. 【答案】;
【解析】由作图可知,垂直平分线段,
,
设,
,,
,
在中,
,
,
解得,或(舍弃),
.
故答案为:
【点评】本题考查作图基本作图,线段的垂直平分线的性质,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
17. 【答案】;
【解析】作于,连接,
,
,
,
,
,
,
,
的面积等于,,
,
,
,
,
,
,
.
故答案为:
【点评】本题考查了反比例函数系数的几何意义,三角形的面积,等腰三角形的性质,正确的作出辅助线是解题的关键.
18. 【答案】;
【解析】 ,点是的中点,矩形的面积等于,
和的面积都等于,
点是的中点,
的面积等于,
同理可得的面积为,
的面积为,
的面积为.
故答案为:
【点评】考查了矩形的性质,规律型:图形的变化类,三角形的面积,本题难点是得到的面积,的面积,,的面积.
三、 解答题
19. 【答案】答案见解析
【解析】原式
,
当时,原式.
【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
20. 【答案】(1)
(2)
(3)
(4)
【解析】(1)本次共调查学生(名).
故答案为:
(2)扇形统计图中,等级所对应的扇形的圆心角为.
故答案为:
(3)等级人数为(名).
补全图形如下:
(4)画树状图为:
共有种等可能的结果数,其中恰好同时选中甲、乙两名同学的结果数为,
所以恰好同时选中甲、乙两名同学的概率.
【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率.也考查了统计图.
21. 【答案】(1)
(2)
【解析】(1)设每本甲种词典的价格为元,每本乙种词典的价格为元,
依题意,得:,
解得:.
答:每本甲种词典的价格为元,每本乙种词典的价格为元.
(2)设学校购买甲种词典本,则购买乙种词典本,
依题意,得:,
解得:.
答:学校最多可购买甲种词典本.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
22. 【答案】距离是海里
【解析】过点作于,如图所示:
由题意得:,
,
,
在中,,,
,
,
是等腰直角三角形,
(海里).
货船与港口之间的距离是海里.
【点评】本题考查了解直角三角形的应用方向角问题、等腰直角三角形的判定与性质等知识;通过作辅助线得出直角三角形是解题的关键.
23. 【答案】(1)
(2)当每瓶洗手液的售价定为元时,最大利润为元.
【解析】(1)设与之间的函数关系式为,根据题意得:
,
解得:,
与之间的函数关系为;
(2)根据题意得:,
,
抛物线开口向下,有最大值,
当时,随着的增大而增大,
且为整数,
当时,有最大值,
即:,
当每瓶洗手液的售价定为元时,超市销售该品牌洗手液每天销售利润最大,最大利润为元.
【点评】本题主要考查二次函数的应用,解题的关键是熟练掌握待定系数法求函数解析式及根据总利润的相等关系列出函数解析式、利用二次函数的性质求最值问题.
24. 【答案】(1)答案见解析
(2)答案见解析
【解析】(1)证明:连接,
四边形是平行四边形,
,,
,
,
,
,
,
,
,
,
,
是的半径,
与相切;
(2)解: ,,
是等边三角形,
,,
,
,,
,
,
,
,
,
,,
,
.
【点评】本题考查了切线的判定和性质,平行四边形的性质,全等三角形的判定和性质,等边三角形的判定和性质,扇形的面积的计算,熟练掌握切线的判定定理是解题的关键.
25. 【答案】(1)
(2)答案见解析
(3)
【解析】(1)连接,如图① 所示:
,,,
,
、、、四点共圆,
,,
,
,
,,
是等腰直角三角形,
,
,
,
;
(2),理由如下:
在上截取,连接,过点作于,如图② 所示:
,,
,
,
在和中,,
,
,,
,
,
,
,
,
,
,
,,
在中,,,
,
,,
;
(3)分两种情况:
① 当点在线段上时,
在上截取,连接,过点作于,如图② 所示:
由(2)得:,
,
,
,
;
② 当点在线段的延长线上时,
在射线上截取,连接,过点作于,如图③ 所示:
同① 得:,,
,
;
综上所述,当,时,的值为或.
【点评】本题是三角形综合题目,考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质、四点共圆、圆周角定理、三角函数定义等知识;本题综合性强,构造全等三角形是解题的关键.
26. 【答案】(1)
(2)
(3)答案见解析
【解析】(1)把点和代入中,
得到,
解得,
抛物线的解析式为.
(2)如图① 中,设抛物线的对称轴交轴于,与交于点.
,
顶点,,
.,
,
,
,
,
,
,
直线的解析式为,
由,解得或,
.
(3)如图② 中,当时,点在第一象限,此时,,重合,由题意,可得, ,利用平移的性质可得.
如图② 中,当时,点在对称轴右侧,由题意,可得,利用平移的性质可得.
如图② 中当时,点在对称轴左侧,点在对称轴上,由题意,可得,,利用平移的性质,可得.
综上所述,满足条件的点的坐标为,或,或.
【点评】本题属于二次函数综合题,考查了待定系数法,解直角三角形,矩形的判定和性质等知识,解题的关键是学会构建一次函数,利用方程组确定交点坐标,学会用分类讨论的思想思考问题,属于中考压轴题.








