初中数学人教版八年级下册16.3 二次根式的加减精品ppt课件

这是一份初中数学人教版八年级下册16.3 二次根式的加减精品ppt课件，共28页。PPT课件主要包含了素养目标，a+3b，解由题意得即，完成下列各题，二次根式的加减，化成最简二次根式，逆用分配律，解列式如下，用分配律合并，整式加减等内容，欢迎下载使用。

有八只小白兔，每只身上都标有一个最简二次根式，你能根据被开方数的特征将这些小白兔分到四个不同的栅栏里吗？
1. 理解二次根式可以合并的条件.
3. 能熟练地进行二次根式的加减法运算.
2. 类比整式的合并同类项，掌握二次根式的加减运算法则.
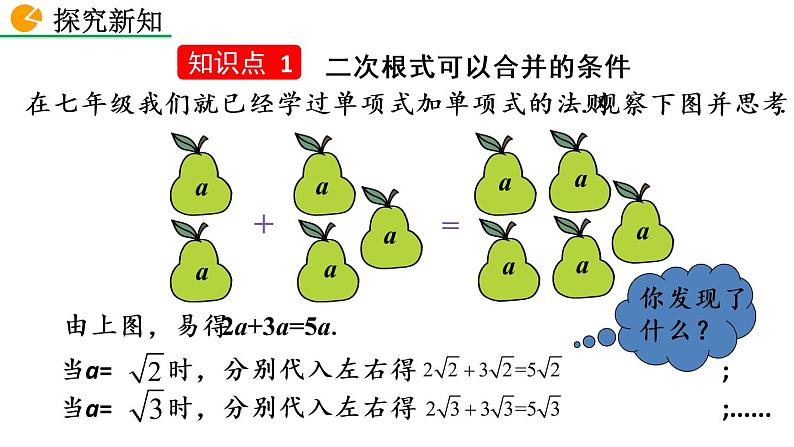
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图，易得2a+3a=5a.
当a= 时，分别代入左右得 ;当a= 时，分别代入左右得 ;
二次根式可以合并的条件
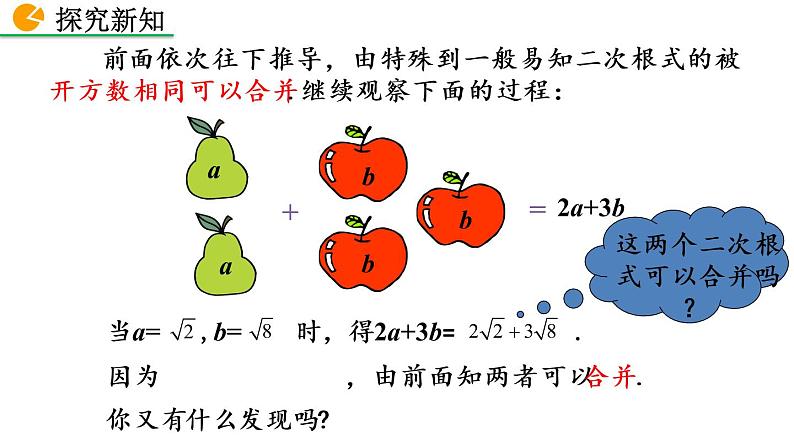
因为 ，由前面知两者可以合并.
当a= ,b= 时，得2a+3b= .
前面依次往下推导，由特殊到一般易知二次根式的被开方数相同可以合并.继续观察下面的过程：
你又有什么发现吗?

将二次根式化成最简二次根式，如果被开方数相同，则这样的二次根式可以合并.
注意：1.判断几个二次根式是否可以合并，一定都要化为最简二次根式再判断;
2.合并的方法与合并同类项类似，把根号外的因数(式)相加，根指数和被开方数(式)不变.如：
提示：可以合并的二次根式中字母取值的方法：利用被开方数相同，根指数都为2列关于字母的方程（组）求解即可.
现有一块长7.5dm、宽5dm的木板，能否采用如图的方式，在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板？
【讨论】 1. 怎样列式求两个正方形边长的和?
【讨论】2.所列算式能直接进行加减运算吗?如果不能,把式中各个二次根式化成最简二次根式后，再试一试(说出每步运算的依据）.
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板．
化为最简二次根式
依据：二次根式的性质、分配律和整式加减法则.
基本思想：把二次根式加减问题转化为整式加减问题．
二次根式的加减法法则:
一般地，二次根式加减时，可以先将二次根式化成最简二次根式，再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简；
(2)找——找出被开方数相同的二次根式；
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
二次根式的加减混合运算
解：①当腰长为 时， ∵ ∴此时能构成三角形，周长为 ②当腰长为 时， ∵ ∴此时能构成三角形，周长为
如图，两个圆的圆心相同，它们的面积分别是8cm2和18cm2，求圆环的宽度d(两圆半径之差).
解：由题意得3a-8=17-2a,∴a=5，∴∴20-2x≥0，x-5＞0，∴5＜x≤10.
已知a,b,c满足 .(1)求a,b,c的值；(2)以a,b,c为三边长能否构成三角形？若能构成三角形，求出其周长；若不能，请说明理由.
解：(1)由题意得 ；
解：∵a*b= ，∴（2*3）－（27*32）===