2021版新高考数学（山东专用）一轮学案：第一章第三讲　逻辑联结词、全称量词与存在量词


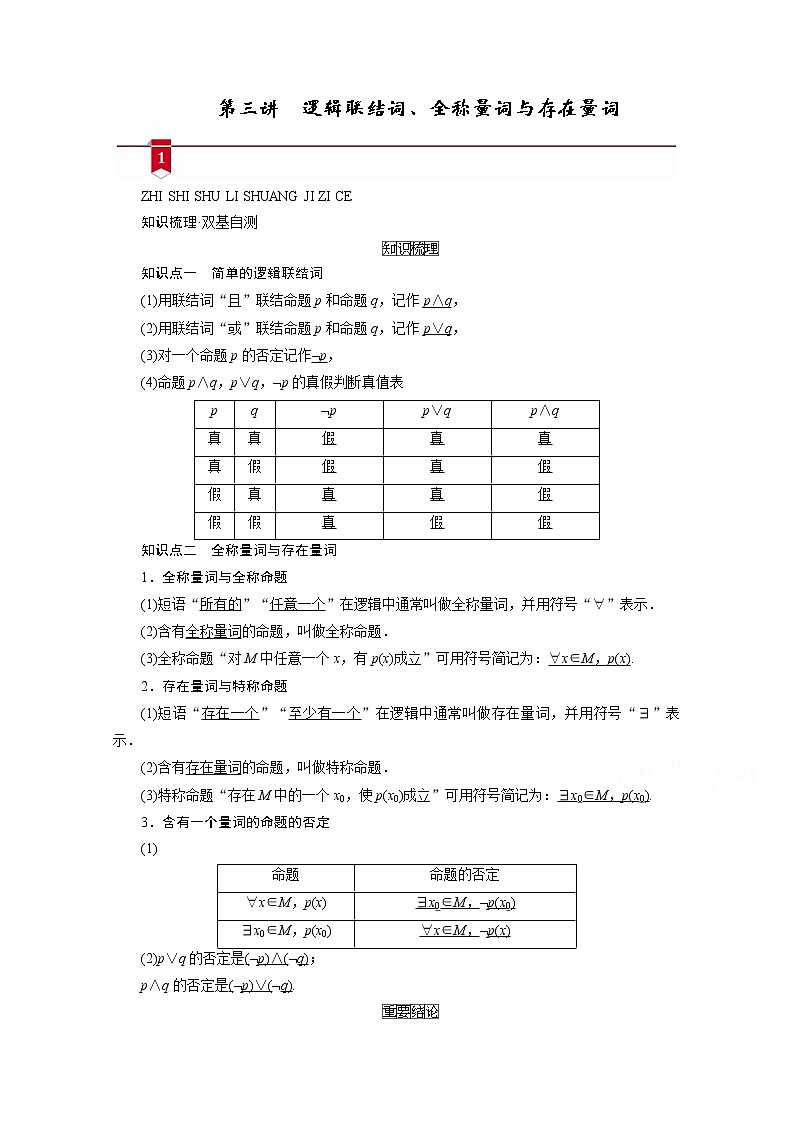
第三讲　逻辑联结词、全称量词与存在量词
ZHI SHI SHU LI SHUANG JI ZI CE
知识梳理·双基自测

知识点一　简单的逻辑联结词
(1)用联结词“且”联结命题p和命题q，记作p∧q，
(2)用联结词“或”联结命题p和命题q，记作p∨q，
(3)对一个命题p的否定记作¬p，
(4)命题p∧q，p∨q，¬p的真假判断真值表
p
q
¬p
p∨q
p∧q
真
真
假
真
真
真
假
假
真
假
假
真
真
真
假
假
假
真
假
假
知识点二　全称量词与存在量词
1．全称量词与全称命题
(1)短语“所有的”“任意一个”在逻辑中通常叫做全称量词，并用符号“∀”表示．
(2)含有全称量词的命题，叫做全称命题．
(3)全称命题“对M中任意一个x，有p(x)成立”可用符号简记为：∀x∈M，p(x).
2．存在量词与特称命题
(1)短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词，并用符号“∃”表示．
(2)含有存在量词的命题，叫做特称命题．
(3)特称命题“存在M中的一个x0，使p(x0)成立”可用符号简记为：∃x0∈M，p(x0).
3．含有一个量词的命题的否定
(1)
命题
命题的否定
∀x∈M，p(x)
∃x0∈M，¬p(x0)
∃x0∈M，p(x0)
∀x∈M，¬p(x)
(2)p∨q的否定是(¬p)∧(¬q)；
p∧q的否定是(¬p)∨(¬q).

1．逻辑联结词与集合的关系．
(1)“或”与集合的“并”密切相关，集合的并集是用“或”来定义的，命题“p∨q”为真有三个含义：只有p成立，只有q成立，p、q同时成立；
(2)“且”与集合的“交”密切相关，集合的交集是用“且”来定义的，命题p∧q为真表示p、q同时成立；
(3)“非”与集合中的补集相类似．
2．常用短语的否定词
若给定
语为
等于
大于
是
且
或
一定
都是
至多
有一个
至少
有一个
至多
有n个
其否定
语为
不等
于
小于或
等于
不是
或
且
一定
不
不都
是
至少有
两个
没有
至少有
n＋1个

题组一　走出误区
1．(多选题)下列判断正确的是(　ABD　)
A．命题“2021≥2020”是真命题
B．命题p和¬p不可能都是真命题
C．“全等三角形的面积相等”是特称命题
D．命题¬ (p∧q)是假命题，则命题p，q都是真命题
题组二　走进教材
2．(选修2－1P23T2改编)下列命题中的假命题是(　C　)
A．∃x0∈R，lg x0＝1 B．∃x0∈R，sin x0＝0
C．∀x∈R，x3>0 D．∀x∈R,2x>0
[解析]　对于C，任意x∈R，x3∈R，故选C．
3．(选修2－1P18A1(3)，改编)已知p：2是偶数，q：2是质数，则命题¬p，¬q，p∨q，p∧q中真命题的个数为(　B　)
A．1 B．2
C．3 D．4
[解析]　命题p是真命题，q是真命题，因此命题¬p，¬q都是假命题，p∨q，p∧q都是真命题，故选B．
题组三　考题再现
4．(2019·全国卷Ⅲ，5分)记不等式组表示的平面区域为D．命题p：∃(x，y)∈D,2x＋y≥9；命题q：∀(x，y)∈D,2x＋y≤12.下面给出了四个命题
①p∨q　②(¬p)∨q　③p∧(¬q)　④(¬p)∧(¬q)
这四个命题中，所有真命题的编号是(　A　)
A．①③ B．①②
C．②③ D．③④
[解析]　

方法一：作出不等式组表示的平面区域D如图中阴影部分所示，直线2x＋y＝9和直线2x＋y＝12均穿过了平面区域D，不等式2x＋y≥9表示的区域为直线2x＋y＝9及其右上方的区域，所以命题p正确；不等式2x＋y≤12表示的区域为直线2x＋y＝12及其左下方的区域，所以命题q不正确．所以命题p∨q和p∧(¬q)正确．故选A．
方法二：在不等式组表示的平面区域D内取点(7,0)，点(7,0)满足不等式2x＋y≥9，所以命题p正确；点(7,0)不满足不等式2x＋y≤12，所以命题q不正确．所以命题p∨q和p∧(¬q)正确．故选A．
5．(2016·浙江，5分)命题“∀x∈R，∃n∈N*，使得n≥x2”的否定形式是(　D　)
A．∀x∈R，∃n∈N*，使得n B．∀x∈R，∀x∈N*，使得n C．∃x∈R，∃n∈N*，使得n D．∃x∈R，∀n∈N*，使得n [解析]　根据含有量词的命题的否定的概念可知，选D．
6．(2015·山东，5分)若“∀x∈[0，]，tan x≤m”是真命题，则实数m的最小值为1.
[解析]　由已知可得m≥tan x(x∈[0，])恒成立．设f(x)＝tan x(x∈[0，])，显然该函数为增函数，故f(x)的最大值为f()＝tan ＝1，由不等式恒成立可得m≥1，即实数m的最小值为1.


KAO DIAN TU PO HU DONG TAN JIU
考点突破·互动探究
　　　　　　 　　　 　　　　　　 　　　　　


考点一　含逻辑联结词的命题及其真假判断——自主练透
例1 (1)在一次跳高比赛前，甲、乙两名运动员各试跳了一次．设命题p表示“甲的试跳成绩超过2米”，命题q表示“乙的试跳成绩超过2米”，则命题p∨q表示(　D　)
A．甲、乙两人中恰有一人的试跳成绩没有超过2米
B．甲、乙两人中至少有一人的试跳成绩没有超过2米
C．甲、乙两人中两人的试跳成绩都没有超过2米
D．甲、乙两人中至少有一人的试跳成绩超过2米

(2)若命题“p∨q”是真命题，“¬p”为真命题，则(　B　)
A．p真，q真 B．p假，q真
C．p真，q假 D．p假，q假
(3)(多选题)已知命题p：∀x>0，ln(x＋1)>0；命题q：若a>b，则a2>b2.下列命题为假命题的是(　ACD　)
A．p∧q B．p∧(¬q)
C．(¬p)∧q D．(¬p)∧(¬q)
(4)(2020·四川成都双流中学模拟)在射击训练中，某战士射击了两次，设命题p是“第一次射击击中目标”，命题q是“第二次射击击中目标”，则命题“两次射击中至少有一次没有击中目标”为真命题的充要条件是(　A　)
A．(¬p)∨(¬q)为真命题 B．p∨(¬q)为真命题
C．(¬p)∧(¬q)为真命题 D．p∨q为真命题
[解析]　(1)因为命题p表示“甲的试跳成绩超过2米”，命题q表示“乙的试跳成绩超过2米”，所以命题p∨q表示“甲、乙两人中至少有一人的试跳成绩超过2米”，故选D．
(2)“¬p”为真命题，所以p为假命题；又因为命题“p∨q”是真命题，所以q为真命题．
(3)∵x>0，∴x＋1>1，∴ln(x＋1)>ln 1＝0，∴命题p为真命题．当a＝1，b＝－2时，a>b成立，但a2>b2不成立．∴命题q为假命题．∴命题p∧(¬q)为真命题，其余三个都是假命题．故选A、C、D．
(4)∵命题p是“第一次射击击中目标”，命题q是“第二次射击击中目标”，则命题¬p是“第一次射击没击中目标”，命题¬q是“第二次射击没击中目标”，∴命题“两次射击中至少有一次没有击中目标”是(¬p)∨(¬q)，故选A．

名师点拨 ☞
“p∨q”“p∧q”“ ¬p”形式命题真假的判断步骤
(1)确定命题的构成形式．
(2)判断其中命题p、q的真假．
(3)确定“p∧q”“p∨q”“ ¬p”等形式命题的真假．p∧q中p、q有一假为假，p∨q中，p、q有一真为真，p与¬p必定是一真一假．
考点二　含有一个量词的命题——多维探究
角度1　全称命题、特称命题的真假
例2 (多选题)(2020·吉林长春外国语学校高三上期中改编)下列命题中，假命题是(　ABD　)
A．∃x0∈R，sin2 ＋cos2 ＝
B．∀x∈(0，π)，sin x>cos x
C．∀x∈(0，＋∞)，x2＋1>x
D．∃x0∈R，x＋x0＝－1
[解析]　对于A，由同角三角函数和平方关系，我们知道∀x∈R，sin2 ＋cos2 ＝1，所以A为假命题；对于B，取特殊值，当x＝时，sin x＝cos x＝，所以B为假命题；对于C，一元二次方程根的判别式Δ＝1－4＝－3<0，所以原方程没有实数根，所以C为真命题；对于D，判别式Δ＝1－4＝－3<0，所以D错误．故选A、B、D．
角度2　含一个量词的命题的否定
例3 (1)(2020·湖北部分重点中学高三测试)已知p：∃x0∈R,3x0 A．∀x∈R,3xx
C．∀x∈R,3x≥x3 D．∃x0∈R,3x0≥x
(2)(2020·陕西部分学校摸底)命题“∀x∈R，≥0”的否定是(　D　)
A．∃x∈R，<0 B．∃x∈R,0 C．∀x∈R，≤0 D．∃x∈R,0 [解析]　(1)因为特称命题的否定为全称命题，所以¬p：∀x∈R,3x≥x3，故选C．
(2)∀x∈R，≥0的否定是∃x0∈R，使不大于等于0，包括小于零和无意义，即∃x0∈R,0
名师点拨 ☞
全(特)称命题真假的判断方法

全称命题
特称命题
真假
真
假
真
假
法一
证明所有对象使命题为真
存在一个对象使命题为假
存在一个对象使命题为真
证明所有对象使命题为假
法二
否定为假
否定为真
否定为假
否定为真
注：当判断原命题的真假有困难时，可通过判断它的逆否命题的真假来实现．
角度3　含参命题中参数的取值范围
例4 (1)(2019·湖南邵阳高三上10月联考)若命题“∃x0∈R，x＋2mx0＋m＋2<0”为假命题，则m的取值范围是(　C　)
A．(－∞，－1]∪[2，＋∞) B．(－∞，－1)∪(2，＋∞)
C．[－1,2] D．(－1,2)
(2)已知f(x)＝ln(x2＋1)，g(x)＝()x－m，若对于∀x1∈[0,3]，∃x2∈[1,2]，使得f(x1)≥g(x2)，则实数m的取值范围是(　A　)
A．[，＋ ∞) B．(－∞，]
C．[，＋∞) D．(－∞，]
[解析]　(1)由已知得不等式，
x＋2mx0＋m＋2<0无解，
所以Δ≤0即(2m)2－4(m＋2)≤0，
解得－1≤m≤2，故选C．
(2)当x∈[0,3]时，f(x)min＝f(0)＝0，
当x∈[1,2]时，g(x)min＝g(2)＝－m，
由f(x)min≥g(x)min得0≥－m，所以m≥.
[例4(2)引申1]把本例中“∃x2∈[1,2]”改为：“∀x2∈[1,2]”，其他条件不变，则实数m的取值范围是m≥.
[解析]　当x∈[0,3]时，f(x)min＝f(0)＝0，
当x∈[1,2]时，g(x)max＝g(1)＝－m，
由f(x)min≥g(x)max得0≥－m，所以m≥.
[例4(2)引申2]把本例中，∀x1∈[0,3]改为∃x1∈[0,3]其他条件不变，则实数m的取值范围是m≥－ln 10.
[解析]　当x∈[0,3]时，f(x)max＝f(3)＝ln 10，
当x∈[1,2]时，g(x)min＝g(2)＝－m，
由f(x)max≥g(x)min得ln 10≥－m，
所以m≥－ln 10.答案：m≥－ln 10
[例4(2)引申3]把本例中，∀x1∈[0,3]，∃x2∈[1,2]改为∃x1∈[0,3]，∀x2∈[1,2]，其他条件不变，则实数m的取值范围是m≥－ln 10.
[解析]　当x∈[0,3]时，f(x)max＝f(3)＝ln 10，
当x∈[1,2]时，g(x)max＝g(1)＝－m，
由f(x)max≥g(x)max，得ln 10≥－m，
所以m≥－ln 10.答案：m≥－ln 10

名师点拨 ☞
根据复合命题的真假求参数范围的步骤
(1)先求出每个简单命题为真命题时参数的取值范围．
(2)再根据复合命题的真假确定各个简单命题的真假情况(有时不一定只有一种情况)．
(3)最后由(2)的结论求出满足条件的参数取值范围．
变式训练1〕
(1)(角度1)下列命题中为假命题的是(　B　)
A．∀x∈R，ex>0 B．∀x∈N，x2>0
C．∃x0∈R，ln x0<1 D．∃x0∈N*，sin＝1
(2)(角度2)(2019·江西南昌莲塘一中10月月考)命题p：∃x0∈N，x<1，则¬p是(　D　)
A．∃x0∈N，x≥1 B．∃x0∈N，x>1
C．∀x∈N，x2>1 D．∀x∈N，x2≥1
(3)(角度3)已知命题p：“∀x∈[1,2]，x2－a≥0”，命题q：“∃x0∈R，x＋2ax0＋2－a＝0”．若命题“(¬p)∧q”是真命题，则实数a的取值范围是(　C　)
A．(－∞，－2)∪{1} B．(－∞，－2]∪[1,2]
C．(1，＋∞) D．[－2,1]
(4)(角度3)已知函数f(x)＝x2＋2x＋a和g(x)＝2x＋，对∀x1∈[－1，＋∞)，∃x2∈R使g(x1)＝f(x2)成立，则实数a的取值范围是(－∞，－1].
[解析]　(1)对于选项A，由函数y＝ex的图象可知，∀x∈R，ex>0，故选项A为真命题；对于选项B，当x＝0时，x2＝0，故选项B为假命题；对于选项C，当x0＝时，ln ＝－1<1，故选项C为真命题；对于选项D，当x0＝1时，sin＝1，故选项D为真命题，故选B．
(2)特称命题的否定是全称命题，所以¬p是∀x∈N，x2≥1.故选D．
(3)命题p为真命题时a≤1；命题q：“∃x0∈R，x＋2ax0＋2－a＝0”为真命题，即方程x2＋2ax＋2－a＝0有实根，故Δ＝4a2－4(2－a)≥0，解得a≥1或a≤－2.又(¬p)∧q为真命题，即¬p真且q真，所以a>1，即a的取值范围为(1，＋∞)．故选C．
(4)因为f(x)＝x2＋2x＋a＝(x＋1)2＋a－1，
所以f(x)∈[a－1，＋∞)．
因为g(x)＝2x＋在[－1，＋∞)上单调递增，
所以g(x)∈[－2，＋∞)．由题意得a－1≤－2，
所以a≤－1，故实数a的取值范围是(－∞，－1]．



MING SHI JIANG TAN SU YANG TI SHENG
名师讲坛·素养提升
简易逻辑的综合应用
例5 (2019·全国卷Ⅱ，5分)在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测．
甲：我的成绩比乙高．
乙：丙的成绩比我和甲的都高．
丙：我的成绩比乙高．
成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为(　A　)
A．甲、乙、丙 B．乙、甲、丙
C．丙、乙、甲 D．甲、丙、乙
[解析]　依题意，若甲预测正确，则乙、丙均预测错误，此时三人成绩由高到低的次序为甲、乙、丙；若乙预测正确，此时丙预测也正确，这与题意相矛盾；若丙预测正确，则甲预测错误，此时乙预测正确，这与题意相矛盾．综上所述，三人成绩由高到低的次序为甲、乙、丙，选A．

名师点拨 ☞
在一些逻辑问题中，当字面上并未出现“或”“且”“非”字样时，应从语句的陈述中搞清含义，并根据题目进行逻辑分析，找出各个命题之间的内在联系，从而解决问题．
〔变式训练2〕
　(2017·全国卷Ⅱ)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则(　D　)
A．乙可以知道四人的成绩
B．丁可以知道四人的成绩
C．乙、丁可以知道对方的成绩
D．乙、丁可以知道自己的成绩
[解析]　由甲说：“我还是不知道我的成绩”可推知甲看到乙、丙的成绩为“1个优秀、1个良好”．乙看丙的成绩，结合甲的说法，丙为“优秀”时，乙为“良好”；丙为“良好”时，乙为“优秀”，可得乙可以知道自己的成绩．丁看甲的成绩，结合甲的说法，甲为“优秀”时，丁为“良好”；甲为“良好”时，丁为“优秀”，可得丁可以知道自己的成绩．故选D．