2020江苏高考理科数学二轮讲义：专题六第4讲　算法初步

第4讲　算法初步

 [2019考向导航]

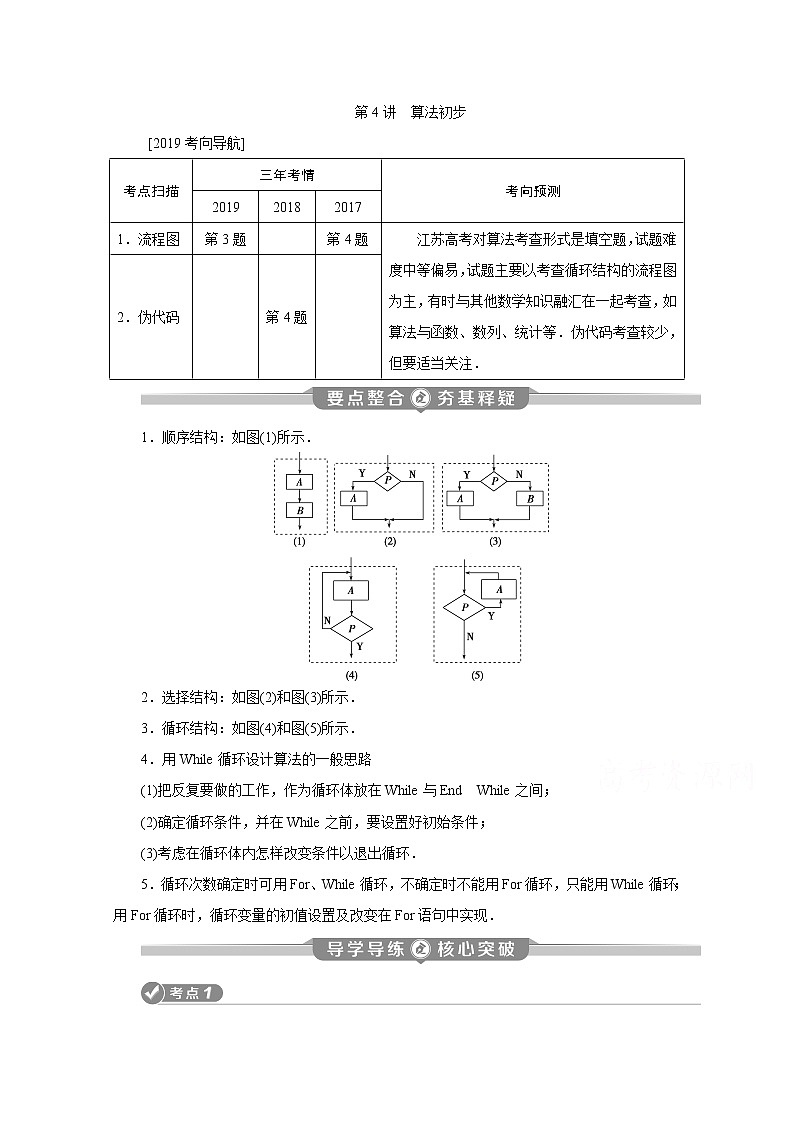
1．顺序结构：如图(1)所示．

2．选择结构：如图(2)和图(3)所示．

3．循环结构：如图(4)和图(5)所示．

4．用While循环设计算法的一般思路

(1)把反复要做的工作，作为循环体放在While与End　While之间；

(2)确定循环条件，并在While之前，要设置好初始条件；

(3)考虑在循环体内怎样改变条件以退出循环．

5．循环次数确定时可用For、While循环，不确定时不能用For循环，只能用While循环；用For循环时，循环变量的初值设置及改变在For语句中实现．

流程图

[典型例题]

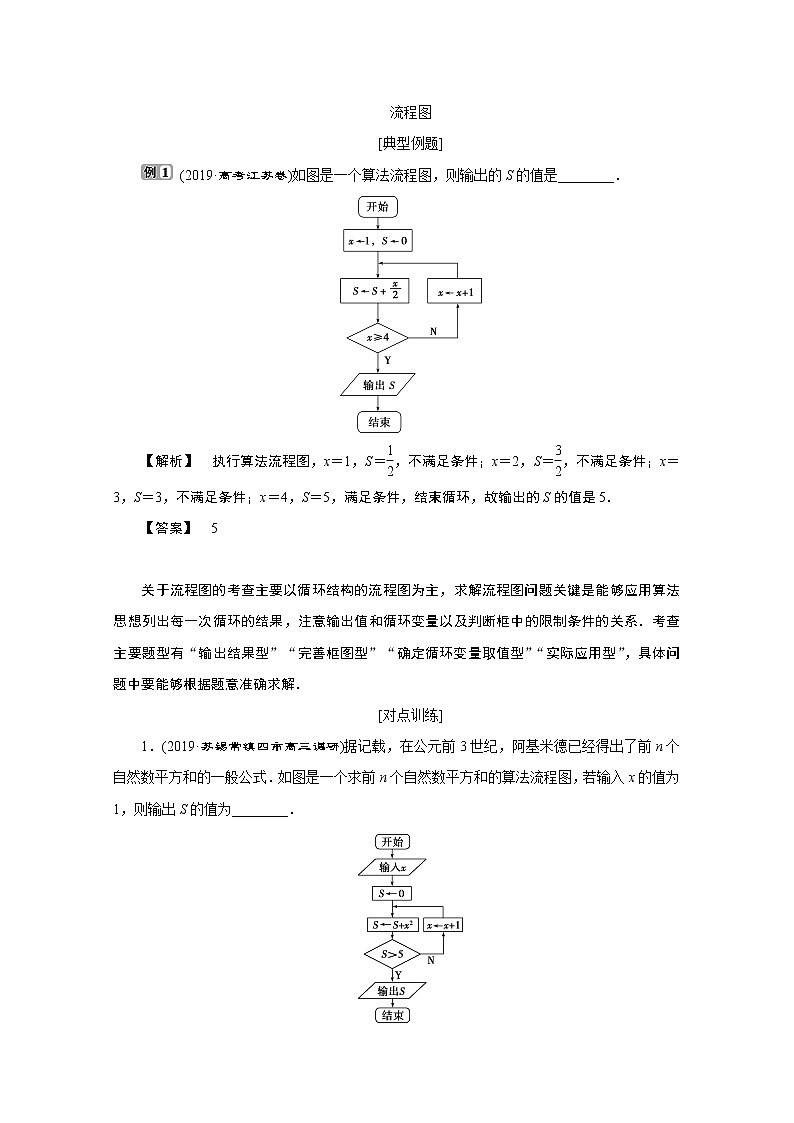
(2019·高考江苏卷)如图是一个算法流程图，则输出的S的值是________．

【解析】　执行算法流程图，x＝1，S＝，不满足条件；x＝2，S＝，不满足条件；x＝3，S＝3，不满足条件；x＝4，S＝5，满足条件，结束循环，故输出的S的值是5．

【答案】　5

关于流程图的考查主要以循环结构的流程图为主，求解流程图问题关键是能够应用算法思想列出每一次循环的结果，注意输出值和循环变量以及判断框中的限制条件的关系．考查主要题型有“输出结果型”“完善框图型”“确定循环变量取值型”“实际应用型”，具体问题中要能够根据题意准确求解．

[对点训练]

1．(2019·苏锡常镇四市高三调研)据记载，在公元前3世纪，阿基米德已经得出了前n个自然数平方和的一般公式．如图是一个求前n个自然数平方和的算法流程图，若输入x的值为1，则输出S的值为________．

[解析] 运行该流程图，x＝1，S＝1；x＝2，S＝5；x＝3，S＝14＞5，结束运行．故输出S的值为14．

[答案] 14

伪代码

[典型例题]

(2018·高考江苏卷)一个算法的伪代码如图所示，执行此算法，最后输出的S的值为________．

【解析】　该伪代码运行3次，第1次，I＝3，S＝2；第2次，I＝5，S＝4；第3次，I＝7，S＝8，结束运行．故输出的S的值为8．

【答案】　8

算法语句包括条件语句和循环语句，不论是哪种语句，只要按照语句的算法规则求解就能顺利解题．　

[对点训练]

2．下列伪代码执行后输出的结果是________．

[解析] n初值是5，S初值是0，每循环一次n减1，S增加，共循环5次，故n＝0．

[答案] 0

1．(2019·泰州模拟)执行如图所示的流程图，则输出的n为________．

[解析] 经过第一次循环得

S＝＝255＞63，n＝2；

经过第二次循环得

S＝＝127＞63，n＝3；

经过第三次循环得

S＝＝63≤63，n＝4，

退出循环，故输出的n＝4．

[答案] 4

2．执行如图所示的流程图，若输出的结果为，则输入的实数x的值是________．

[解析] 由流程图可得要使输出结果为，则

或解得x＝．

[答案] 

3．执行如图所示的流程图，如果输出的a＝341，那么判断框中可以是________．

[解析]　执行流程图后，a1＝4a＋1＝1，k1＝k＋1＝2；a2＝4a1＋1＝5，k2＝k1＋1＝3；a3＝4a2＋1＝21，k3＝k2＋1＝4；a4＝4a3＋1＝85，k4＝k3＋1＝5；a5＝4a4＋1＝341，k5＝k4＋1＝6．要使输出的a＝341，判断框中可以是“k<6”或“k≤5”．

[答案] “k<6”或“k≤5”(答案不唯一)

4．(2019·南通模拟)如图的伪代码运行后输出的结果是________．

[解析] p0＝1，当k＝1时，p1＝1＋2×1－6＝－3；

当k＝4时，p2＝p1＋2×4－6＝－3＋2×4－6＝－1；

当k＝7时，p3＝p2＋2×7－6＝－1＋2×7－6＝7；

当k＝10时，p4＝p3＋2×10－6＝7＋2×10－6＝21．

所以p＝21．

[答案] 21

5．执行如图所示的流程图，输出的M的值为________．

[解析] 由流程图可得：M＝1，k＝0；

k＝1，M＝3×1＋2＝5；k＝2，M＝3×5＋2＝17；

k＝3，M＝3×17＋2＝53；k＝4，M＝3×53＋2＝161．

不满足循环条件，跳出循环，输出M＝161．

[答案] 161

6．执行如图所示的流程图，如果输入的t＝0．01，则输出的n＝________．

[解析] 运行第一次：S＝1－＝＝0．5，m＝0．25，n＝1，S＞0．01；

运行第二次：S＝0．5－0．25＝0．25，m＝0．125，n＝2，S＞0．01；

运行第三次：S＝0．25－0．125＝0．125，m＝0．062 5，n＝3，S＞0．01；

运行第四次：S＝0．125－0．062 5＝0．062 5，m＝0．031 25，n＝4，S＞0．01；

运行第五次：S＝0．031 25，m＝0．015 625，n＝5，S＞0．01；

运行第六次：S＝0．015 625，m＝0．007 812 5，n＝6，S＞0．01；

运行第七次：S＝0．007 812 5，m＝0．003 906 25，n＝7，S＜0．01．输出n＝7．

[答案] 7

7．(2019·盐城中学开学考试)某算法的伪代码如图所示，若输出y的值为1，则输入x的值为________．

[解析] 由题意得算法的功能是求函数y＝的值，故当y＝1时有或，解得x＝－1或x＝2 014．

[答案] －1或2 014

8．执行如图所示的算法流程图，输出的n为________．

[解析] a＝1，n＝1时，条件成立，进入循环体；a＝，n＝2时，条件成立，进入循环体；a＝，n＝3时，条件成立，进入循环体；a＝，n＝4时，条件不成立，退出循环体，此时n的值为4．

[答案] 4

9．如图是寻找“徽数”的流程图，其中“S MOD 10”表示自然数S被10除所得的余数，“S/10”表示自然数S被10除所得的商．则根据如图的流程图，输出的“徽数”S为________．

[解析] 流程图运行如下：S＝10，x＝0，y＝1，S≠3(0＋1＋1)；S＝11，x＝1，y＝1，S≠3(1＋1＋1)；S＝12，x＝2，y＝1，S＝3(2＋1＋1)，此时输出S＝12．

[答案]  12

10．(2019·徐州模拟)如图是统计高三年级2 000名同学某次数学考试成绩的流程图，若输出的结果是560，则这次考试数学分数不低于90分的同学的频率是________．

[解析]  根据流程图可知，输出结果为数学分数低于90分的同学的人数，因此这次考试数学分数不低于90分的同学的人数是2 000－560＝1 440，其频率为＝0．72．

[答案]  0．72

11．(2019·南京调研)如图所示的流程图，若输入n＝7，则输出的n值为________．

[解析]  执行过程为n＝7→n＝5，f(x)＝x5→n＝3，f(x)＝x3→n＝1，f(x)＝x→n＝－1，f(x)＝在(0，＋∞)上单调递减，故输出n＝－1．

[答案] －1

12．按如图所示的程序框图运行后，输出的结果是63，则判断框中的整数M的值是________．

[解析] 由算法流程图知，开始时A＝1，S＝1，此时A≤M，S＝3，A＝2；接下来有A＝2，S＝3，此时A≤M，S＝7，A＝3；接下来有A＝3，S＝7，此时A≤M，S＝15，A＝4；接下来有A＝4，S＝15，此时A≤M，S＝31，A＝5；接下来有A＝5，S＝31，A≤M，S＝63，A＝6，由题意可知输出的结果是63，A>M．故M＝5．

[答案] 5