资料中包含下列文件,点击文件名可预览资料内容





还剩3页未读,
继续阅读
成套系列资料,整套一键下载
人教版八年级下册物理期末复习 第10章 浮力 计算题专练(有答案)-原卷版+解析版
展开
人教版八年级下册物理期末复习 第10章 浮力 计算题专练(有答案)-原卷版+解析版
人教版八年级物理期末复习 第10章 浮力 计算题专练
1.伟大的中华民族正在走向复兴,人民海军走向深蓝。2019年4月23日,为庆祝中国人民海军成立七十周年,中国完全自主研制的055大型驱逐舰首次在山东青岛公开亮相。该舰是中国第一款排水量超过万吨的主力驱逐舰,舰长183m、宽23m,满载时吃水深度为8m,排水量可达12500t。(g取10N/kg,海水密度取ρ海水=1.0×103kg/m3)
(1)求055驱逐舰满载时所受的浮力;
(2)若一架总质量为13t的直升机为了执行侦察任务飞离驱逐舰,求055驱逐舰浸在水里的体积减少了多少。
【考点】8O:阿基米德原理的应用;8S:物体的浮沉条件及其应用.【分析】(1)知道055驱逐舰满载时的排水量,根据F浮=G排=m排g求出所受的浮力;
(2)直升机飞离驱逐舰前后驱逐舰始终漂浮,受到的浮力和自身的重力相等,据此求出直升机飞离驱逐舰后所受浮力的减少量,根据F浮=ρgV排求出055驱逐舰浸在水里的体积减少的量。
【解答】解:
(1)由阿基米德原理可得,055驱逐舰满载时所受的浮力:
F浮=G排=m排g=12500×103kg×10N/kg=1.25×108N;
(2)因直升机飞离驱逐舰前后驱逐舰始终漂浮,受到的浮力和自身的重力相等,
所以,直升机飞离驱逐舰后所受浮力的减少量:
△F浮=G=mg=13×103kg×10N/kg=1.3×105N,
由F浮=ρgV排可得,055驱逐舰浸在水里的体积减少了:
△V排===13m3。
答:(1)055驱逐舰满载时所受的浮力为1.25×108N;
(2)055驱逐舰浸在水里的体积减少了13m3。
本题考查了阿基米德原理和物体浮沉条件的应用,要注意直升机飞离驱逐舰前后驱逐舰所受浮力的变化等于直升机的重力。
2.如图所示,水平桌面上有一个薄壁溢水杯,底面积是8×10﹣3m2,装满水后水深0.1m,总质量是0.95kg。把一个木块(不吸水)轻轻放入水中,待木块静止时,从杯中溢出水的质量是0.1kg。求:(水的密度ρ=1.0×103kg/m3,g取10N/kg)
(1)水对溢水杯底的压力。
(2)木块受到的浮力。
(3)溢水杯对桌面的压力。
【分析】(1)知道水深,利用求p=ρgh水对溢水杯底的压强,再利用F=pS求水对溢水杯底的压力;
(2)根据阿基米德原理求木块所受的浮力;
(3)因为木块漂浮在水面上,所以F浮=G排=G木,溢水杯对桌面的压力等于原来溢水杯和水的总重力加上木块的重力再减去排开水的重力。
【解答】解:
(1)水对溢水杯底的压强:
p=ρgh=1.0×103kg/m3×10N/kg×0.1m=1000Pa,
由p=可得水对溢水杯底的压力:
F=pS=1000Pa×8×10﹣3m2=8N;
(2)由阿基米德原理可得木块所受的浮力:
F浮=G排=m排g=m溢g=0.1kg×10N/kg=1N;
(3)因为木块漂浮在水面上,所以F浮=G排=G木,
所以此时溢水杯对桌面的压力:
F=G+G木﹣G排=G=mg=0.95kg×10N/kg=9.5N。
答:(1)水对溢水杯底的压力为8N;
(2)木块受到的浮力为1N;
(3)溢水杯对桌面的压力为9.5N。
本题考查了重力公式、压强定义式、液体压强公式、阿基米德原理、物体漂浮条件的应用,要明确装满水的溢水杯在放入木块前后对桌面的压力相同。
3.某型号一次性声呐,其内部有两个相同的空腔,每个空腔的容积为2×10﹣3m3,每个空腔的侧上方都用轻薄易腐蚀材料制成的密封盖密封,密封盖在海水中浸泡24小时后,将被海水完全腐蚀。
某次公海军事演习,反潜飞机向海中投入该声呐,声呐在海中静止后露出整个体积的,声呐处于探测状态,如图甲所示,24小时后,声呐没入海中处于悬浮状态,声呐停止工作,如图乙所示,再经过24小时后,声呐沉入海底,如图丙所示。已知ρ海水=1.1×103kg/m3,g取10N/kg,问:
(1)每个空腔能容纳海水的重量有多大?
(2)声呐整个体积有多大?
(3)图甲中,声呐有多重?
(4)图丙中,海底对声呐的支持力有多大?
【考点】8O:阿基米德原理的应用;8S:物体的浮沉条件及其应用.【分析】(1)知道空腔的容积,由G=mg=ρVg求所容纳的海水的重力;
(2)在把声呐当作一个整体,这个整体包括两个空腔和其余部分,没有海水进入时,这个整体包含两个空腔;海水进入后,这个整体包括进入空腔的海水,图甲中,声呐漂浮,所受的浮力与重力相等,根据图乙所示,声呐在海水中悬浮,此时下方的密封盖被海水腐蚀,所受的浮力等于声呐自身重力和第一个空腔内的海水重力之和,据此解题;
(3)图甲中,声呐漂浮且有体积露出水面,由F浮=G求解;
(4)图丙中,计算此时声呐的总重力,由F支=G﹣F浮求解。
【解答】解:
(1)由题知,每个空腔的容积为V=2×10﹣3m3,
每个空腔能容纳海水的重量:
G海水=m海水g=ρ海水V腔g=1.1×103kg/m3×2×10﹣3m3×10N/kg=22N;
(2)设声呐的整个体积为V,声呐的重力为G声,
图甲中,声呐漂浮(下方的密封盖浸在海水中),且声呐在海中静止后露出整个体积的,
则:G声=F浮=ρ海水g(1﹣)V=ρ海水gV﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①,
图乙中,24小时后,下方的密封口被腐蚀,下方空腔充满海水,声呐悬浮,把声呐和进入的海水作为一个整体(即此时下方空腔内的海水作为声呐的一部分);
则由悬浮条件可得:F浮1=G总1=G声+G海水=ρ海水gV+22N﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②,
而此时声呐浸没在海水中,所以F浮1=ρ海水gV﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣③,
可得:ρ海水gV=ρ海水gV+22N,
解得:V=8×10﹣3m3;
(3)图甲中,声呐漂浮且有体积露出水面,
G声=F浮=ρ海水g(1﹣)V=×1.1×103kg/m3×10N/kg×8×10﹣3m3=66N;
(4)图丙中,声呐上方的密封盖也浸没在海水中,再经过24小时,密封盖也被腐蚀,把声呐和进入的海水作为一个整体(即此时两个空腔内的海水作为声呐的一部分);
则可知声呐的总重力:
G总2=G声+2×G海水=66N+2×22N=110N,
声呐受到的浮力:F浮1=ρ海水gV=1.1×103kg/m3×10N/kg×8×10﹣3m3=88N,
海底对声呐的支持力:F支=G总2﹣F浮1=110N﹣88N=22N。
答:(1)每个空腔能容纳海水的重量有22N;
(2)声呐整个体积为8×10﹣3m3;
(3)图甲中,声呐的重力为66N;
(4)图丙中,海底对声呐的支持力为22N。
本题考查阿基米德原理和物体的漂浮特点的应用,综合性强,难度较大。
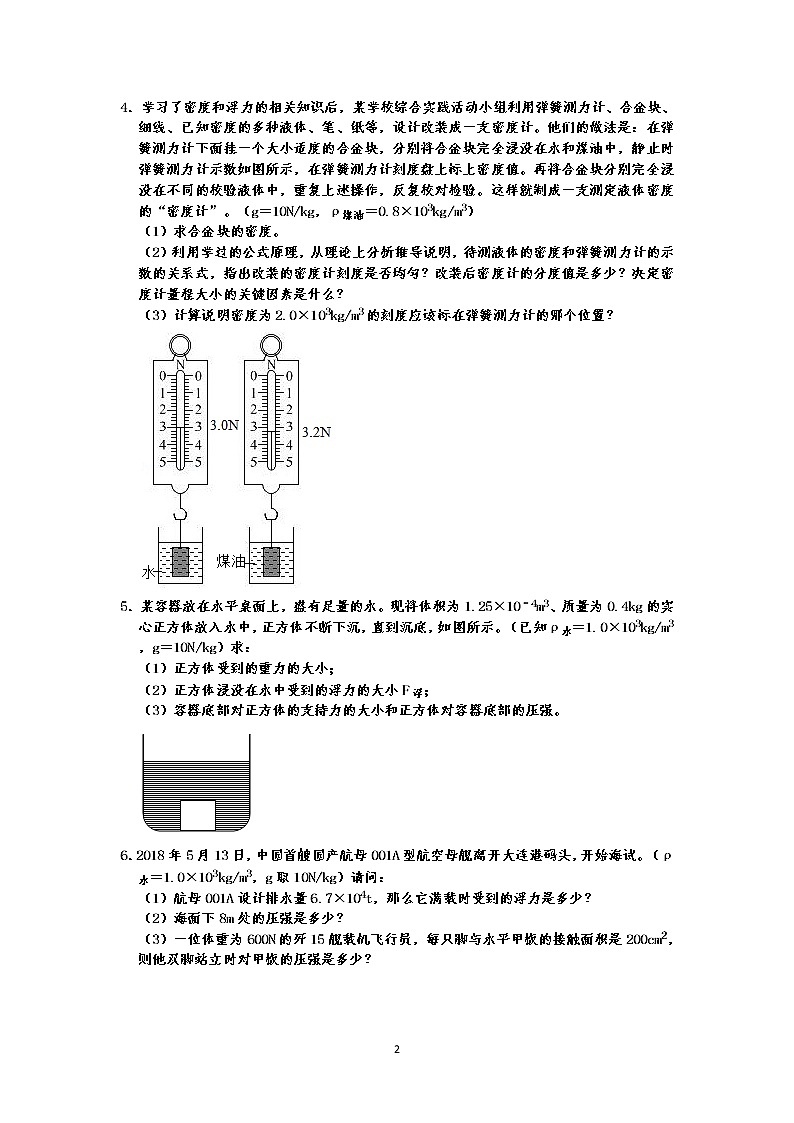
4.学习了密度和浮力的相关知识后,某学校综合实践活动小组利用弹簧测力计、合金块、细线、已知密度的多种液体、笔、纸等,设计改装成一支密度计。他们的做法是:在弹簧测力计下面挂一个大小适度的合金块,分别将合金块完全浸没在水和煤油中,静止时弹簧测力计示数如图所示,在弹簧测力计刻度盘上标上密度值。再将合金块分别完全浸没在不同的校验液体中,重复上述操作,反复校对检验。这样就制成一支测定液体密度的“密度计”。(g=10N/kg,ρ煤油=0.8×103kg/m3)
(1)求合金块的密度。
(2)利用学过的公式原理,从理论上分析推导说明,待测液体的密度和弹簧测力计的示数的关系式,指出改装的密度计刻度是否均匀?改装后密度计的分度值是多少?决定密度计量程大小的关键因素是什么?
(3)计算说明密度为2.0×103kg/m3的刻度应该标在弹簧测力计的哪个位置?
【考点】8O:阿基米德原理的应用.【分析】(1)根据称重法测浮力F=G﹣F浮和阿基米德原理求出物体的体积和G,根据ρ=求出合金块的密度;
(2)由上得出:F示=4N﹣ρ液×10N/kg×10﹣4 m3;据此得出待测液体的密度和弹簧测力计的示数的关系:
分析这个关系式确定密度计刻度是均匀的;
由这个关系式,当最示数最大和最小时得出液体密度,从而得出改装后密度计的分度值;
由关系式,决定密度计量程大小的关键因素;
(3)把ρ液=2.0×103kg/m3代入关系式得了密度为2.0×103kg/m3的刻度应该标在弹簧测力计的位置。
【解答】解:(1)根据称重法测浮力F=G﹣F浮和阿基米德原理有:
3.0N=G﹣ρ水gV=G﹣1.0×103kg/m3×10N/kg×V﹣﹣﹣﹣①
3.2N=G﹣ρ煤油gV=G﹣0.8×103kg/m3×10N/kg×V﹣﹣﹣﹣②;
由①②得:V=10﹣4 m3;G=4N,
合金块的密度:
ρ===4×103kg/m3;
(2)由②得:F示=4N﹣ρ液×10N/kg×10﹣4 m3;
故待测液体的密度和弹簧测力计的示数的关系:
ρ液=4×103kg/m3﹣F示×103 kg/(N•m3)﹣﹣﹣﹣﹣﹣③,
由③知,
ρ液与F示为一次函数关系,改装的密度计刻度是均匀的;
由③知,当F示=4N时,ρ液=0;
当F示=0时,ρ液=4×103kg/m3;0﹣4N之间有20个格,
改装后密度计的分度值为:
=0.2×103kg/m3;
由③知,决定密度计量程大小的关键因素是合金块的密度;
(3)把ρ液=2.0×103kg/m3代入③得:F示=2.0N,即密度为2.0×103kg/m3的刻度应该标在弹簧测力计的2.0N位置处。
答:(1)合金块的密度为4×103kg/m3;
(2)待测液体的密度和弹簧测力计的示数的关系式为ρ液=4×103kg/m3﹣F示×103 kg/(N•m3),改装的密度计刻度是均匀的;改装后密度计的分度值是=0.2×103kg/m3;决定密度计量程大小的关键因素是合金块的密度;
(3)计算说明密度为2.0×103kg/m3的刻度应该标在弹簧测力计2N的位置。
本题制作一支测定液体密度的“密度计”,考查称重法测浮力、阿基米德原理、密度公式的运用和数据分析,关键是得出测液体的密度和弹簧测力计的示数的关系,有一定难度。
5.某容器放在水平桌面上,盛有足量的水。现将体积为1.25×10﹣4m3、质量为0.4kg的实心正方体放入水中,正方体不断下沉,直到沉底,如图所示。(已知ρ水=1.0×103kg/m3,g=10N/kg)求:
(1)正方体受到的重力的大小;
(2)正方体浸没在水中受到的浮力的大小F浮;
(3)容器底部对正方体的支持力的大小和正方体对容器底部的压强。
【考点】78:重力的计算;86:压强的大小及其计算;8O:阿基米德原理的应用.【分析】(1)知道正方体的质量,利用G=mg即可求出正方体的重力;
(2)正方体浸没在水中,排开水的体积与正方体的体积相等,根据F浮=ρ水gV排求出受到的浮力;
(3)正方体沉在底部,根据重力和浮力利用力的平衡即可求出支持力;
根据力的相互作用可知正方体对容器底部的压力,利用p=计算正方体对容器底部的压强。
【解答】解:(1)正方体的重力G=mg=0.4kg×10N/kg=4N;
(2)正方体浸没在水中,V排=V=1.25×10﹣4m3,
则F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1.25×10﹣4m3=1.25N;
(3)正方体沉在底部,由于处于静止状态,则受力平衡,即G=N+F浮,
所以,N=G﹣F浮=4N﹣1.25N=2.75N;
由于支持力与压力是一对相互作用力,则可知正方体对容器底部的压力F=N=2.75N,
正方体的边长L===0.05m,
则正方体对容器底部的压强p===1.1×103Pa。
答:(1)正方体受到的重力的大小为4N;
(2)正方体浸没在水中受到的浮力的大小F浮=1.25N;
(3)容器底部对正方体的支持力的大小为2.75N,正方体对容器底部的压强为1.1×103Pa。
此题考查浮力和液体压强的计算,关键是浮力公式、液体压强公式和压强定义式的应用,此题难度适中,适合学生训练,是一道好题。
6.2018年5月13日,中国首艘国产航母001A型航空母舰离开大连港码头,开始海试。(ρ水=1.0×103kg/m3,g取10N/kg)请问:
(1)航母001A设计排水量6.7×104t,那么它满载时受到的浮力是多少?
(2)海面下8m处的压强是多少?
(3)一位体重为600N的歼15舰载机飞行员,每只脚与水平甲板的接触面积是200cm2,则他双脚站立时对甲板的压强是多少?
【考点】86:压强的大小及其计算;89:液体的压强的计算;8P:浮力大小的计算.【分析】(1)物体所受浮力大小等于它排开液体所受重力;
(2)根据液体压强公式p=ρgh计算;
(3)根据p=计算;
【解答】解:
(1)根据阿基米德原理可得,该航母满载时受到的浮力:
F浮=G排=m排g=6.7×104×103kg×10N/kg=6.7×108N;
(2)海面下8m处的压强:
p=ρgh=1.0×103kg/m3×10N/kg×8m=8×104Pa;
(3)飞行员每只脚与水平甲板的接触面积是200cm2,
所以飞行员双脚站立的受力面积:S=2×200×10﹣4m2=4×10﹣2m2,
飞行员站立在水平甲板上,对甲板的压力F=G,
站立时对甲板的压强:p====1.5×104Pa;
答:(1)满载时受到的浮力是6.7×108N;
(2)海面下8m处的压强是8×104Pa;
(3)双脚站立时对甲板的压强是1.5×104Pa。
本题考查浮力和压强的知识,关键是将课本知识内容记忆清楚,仔细分析即可。
7.用弹簧测力计悬挂一实心物块,物块下表面与水面刚好接触,如图甲所示。由此处匀速下放物块,直至浸没于水中并继续匀速下放(物块始终未与容器接触)。物块下放过程中,弹簧测力计示数F与物块下表面浸入水中的深度h的关系如图乙所示。求:
(1)物块完全浸没在水中受到的浮力;
(2)物块的密度;
(3)从物块刚好浸没水中到h=10cm过程中,水对物块下表面的压强变化了多少Pa?
【考点】2A:密度的计算;89:液体的压强的计算;8O:阿基米德原理的应用;8P:浮力大小的计算.【分析】(1)由图象可知,弹簧测力计的最大示数,此时物块未浸入水中,物块重力等于最大示数;由图得出物块全浸入时弹簧测力计的示数,利用称重法求受到的浮力;
(2)利用F浮=ρ液V排g求物体的体积,利用G=mg求物体的质量,利用密度公式求物体的密度;
(3)由图乙可知,h1=4cm时物块刚好浸没水中,可求从物块刚好浸没水中到h2=10cm过程中物块下表面变化的深度,利用p=ρgh求水对物块下表面的压强变化。
【解答】解:
(1)由图象可知,弹簧测力计的最大示数F最大=8N,此时物块未浸入水中,则物块重力G=F最大=8N;
物块全浸入时弹簧测力计的示数F示=4N,
受到的浮力:
F浮=G﹣F示=8N﹣4N=4N;
(2)由F浮=ρ水gV排得物块的体积:
V=V排===4×10﹣4m3,
物块的质量:
m===0.8kg,
ρ物===2×103kg/m3;
(3)由图乙可知,h1=4cm时物块刚好浸没水中,从物块刚好浸没水中到h2=10cm过程中,
物块下表面变化的深度△h=h2﹣h1=10cm﹣4cm=6cm=0.06m,
水对物块下表面的压强变化:
△p=ρ水g△h=1×103kg/m3×10N/kg×0.06m=600Pa。
故答案为:(1)物块完全浸没在水中受到的浮力为4N;
(2)物块的密度2×103kg/m3;
(3)从物块刚好浸没水中到h=10cm过程中,水对物块下表面的压强变化了600Pa。
本题考查了重力公式、密度公式、阿基米德原理、液体压强公式的应用,分析图象得出相关信息是关键。
8.将物块竖直挂在弹簧测力计下,在空气中静止时弹簧测力计的示数F1=2.6N.将物块的一部分浸在水中,静止时弹簧测力计的示数F2=1.8N,如图所示,已知水的密度ρ=1.0×103kg/m3,g取10N/kg。
求:(1)物块受到的浮力;
(2)物块浸在水中的体积。
【考点】8O:阿基米德原理的应用;8P:浮力大小的计算.【分析】(1)在空气中静止时弹簧测力计的示数即为物块的重力,又知道物块的一部分浸在水中时弹簧测力计的示数,根据F浮=G﹣F′求出物块受到的浮力;
(2)根据阿基米德原理求出物块排开水的体积即为浸在水中的体积。
【解答】解:(1)由称重法可得物块受到的浮力:
F浮=F1﹣F2=2.6N﹣1.8N=0.8N;
(2)由F浮=ρ水gV排可得,物块浸在水中的体积:
V排===8×10﹣5m3。
答:(1)物块受到的浮力为0.8N;
(2)物块浸在水中的体积为8×10﹣5m3。
本题考查了称重法求浮力公式和阿基米德原理的应用,是一道较为简单的计算题。
9.如图甲所示,拉力F通过滑轮组,将正方体金属块从水中匀速拉出至水面上方一定高度处。图乙是拉力F随时间t变化的关系图象。不计动滑轮的重力、摩擦及水和空气对金属块的阻力,g=10N/kg,求:
(1)金属块完全浸没在水中时受到的浮力大小;
(2)金属块的密度;
(3)如果直接将金属块平放在水平地面上,它对地面的压强大小。
【考点】86:压强的大小及其计算;8P:浮力大小的计算.【分析】(1)当金属块完全露出液面,没有浸入水中时,金属块不受浮力,此时拉力等于重力,即为图中的CD段,据此求出金属块重。
分析绳子拉力随时间t变化的图象,当金属块从水中一直竖直向上做匀速直线运动,但未露出液面,此时金属块排开水的体积不变,由阿基米德原理可知,此时的浮力不变,绳子的拉力也不变。当金属块未露出液面时,拉力等于重力减去浮力,据此结合滑轮组绳子拉力的计算求出浮力大小;
(2)根据阿基米德原理求金属块排开水的体积(金属块的体积),知道金属块的重,利用重力和密度公式求金属块的密度。
(3)金属块平放在水平地面上,对地面的压力等于重力,利用体积公式求出金属块的边长,再利用面积公式求出金属块的底面积,即受力面积,最后利用压强公式计算压强。
【解答】解:
(1)由甲图可知,n=2,不计动滑轮的重力、摩擦及水和空气对金属块的阻力,F=G,
当金属块完全露出液面后,金属块不受浮力,此时拉力等于重力,即为图中的t2﹣t3时刻,
从乙图可知,该金属块重力为:G=2F=2×108N=216N,
当金属块未露出液面时,即为图中的0﹣t1时刻,
则2F′+F浮=G,
所以金属块完全浸没在水中时受到的浮力:F浮=G﹣2F′=216N﹣2×68N=80N;
(2)根据F浮=ρgV排可得,金属块排开水的体积:V排===8×10﹣3m3,
金属块完全浸没在水中,则金属块的体积V=V排=8×10﹣3m3,
则根据G=mg、ρ=可得,金属块的密度为:ρ金===2.7×103kg/m3。
(3)金属块的边长a===0.2m,
则受力面积S=a2=(0.2m)2=0.04m2,
金属块平放在水平地面时对地面的压强:p====5.4×103Pa。
答:(1)金属块完全浸没在水中时受到的浮力80N;
(2)金属块的密度2.7×103kg/m3;
(3)如果直接将金属块平放在水平地面上,它对地面的压强5.4×103Pa。
本题考查了重力、浮力、质量、密度、压强的计算以及阿基米德原理,关键是公式和公式变形的应用,难点是通过图乙确定金属块的重力及绳子受到的拉力、会用称重法计算出金属块受到的浮力。
10.工人师傅利用汽车作为动力,从水中打捞一个正方体物件,绳子通过定滑轮,一端系着物件,另一端拴在汽车上,如图甲所示。汽车拉着物件匀速上升,已知汽车对绳子的拉力F与物件底面距离水底的高度h的变化关系如图乙所示。绳子的体积、绳重及摩擦均忽略不计,g取l0N/kg。求:
(1)该物件的质量是多少?
(2)物件浸没在水中时,受到的浮力为多大?
(3)物件上表面恰好到达水面时,下表面受到水的压强为多少?
【考点】89:液体的压强的计算;8P:浮力大小的计算.【分析】(1)由图甲可知滑轮为定滑轮,则该物件离开水面后的拉力余该物件的重力相等,根据G=mg求质量;
(2)图甲中,滑轮为定滑轮,则在乙图中,拉力较小时且大小不变,说明物体浸没在液体中;5m﹣5.5m,拉力逐渐变大,说明物件在离开液体的过程中,正方体的棱长为0.5m;之后物体脱离液体,拉力与物体的重力相等;根据称重法即可求出物件浸没在水中时受到的浮力;
(3)物件上表面恰好到达水面时,根据乙图得出下表面所处的深度,根据压强公式p=ρgh即可求出下表面受到水的压强。
【解答】解:
(1)该物件离开水面后的拉力F2=2500N,由于图甲中,滑轮为定滑轮,则物体的重力为G=F2=2500N,
则物体质量:
m===250kg;
(2)由图乙知中,物体在水中时拉力F1=1250N;
根据称重法可知物件浸没在水中时受到的浮力:
F浮=G﹣F1=2500N﹣1250N=1250N;
(3)由图乙知中,物件上表面恰好到达水面时,下表面所处的深度为h=5.5m﹣5m=0.5m,
则下表面受到水的压强:
p=ρgh=1×103kg/m3×10N/kg×0.5m=5×103Pa。
答:(1)该物件的质量是250kg;
(2)物件浸没在水中时,受到的浮力为1250N;
(3)物件上表面恰好到达水面时,下表面受到水的压强为5×103Pa。
本题综合考查重力公式、定滑轮、称重法和液体压强公式的应用,关键是从图中获得有效的信息,难度较大。
11.某次物理活动举行了“造船”比赛,他们用的材料是密度为1.5×103kg/m3的橡皮泥,其中王强同学选了一块竖立在水平桌面上的圆柱体橡皮泥,它的底面积为1.0×10﹣3m2高为0.2m,最后造出了最大排水体积为6.0×10﹣4m3的小船。(ρ水=1.0×103kg/m3,g取10Nkg)求:
(1)王强同学所选橡皮泥的质量
(2)橡皮泥对桌面产生的压强。
(3)王强同学造的船在水中最大排水时受到的浮力。
【考点】2B:密度公式的应用;86:压强的大小及其计算;8O:阿基米德原理的应用.【分析】(1)根据V=Sh计算橡皮泥的体积,知道橡皮泥的体积和密度,利用m=ρV求橡皮泥的质量;
(2)利用G=mg求橡皮泥的重力;橡皮泥对桌面产生的压力等于其重力,知道受力面积,再利用p=求橡皮泥对桌面产生的压强;
(3)利用阿基米德原理求最大排水时受到的浮力。
【解答】解:
(1)由题知,圆柱体橡皮泥的底面积为1.0×10﹣3m2,高为0.2m,
则橡皮泥的体积:V=Sh=1.0×10﹣3m2×0.2m=2×10﹣4m3,
由ρ=得橡皮泥的质量:
m=ρV=1.5×103kg/m3×2×10﹣4m3=0.3kg;
(2)橡皮泥的重力:
G=mg=0.3kg×10N/kg=3N,
橡皮泥对桌面的压力:
F=G=3N,
受力面积S=1.0×10﹣3m2,
橡皮泥对桌面产生的压强:
p===3000Pa;
(3)该船在最大排水时受到的浮力:
F浮=ρ水gV排大=1.0×103kg/m3×10N/kg×6.0×10﹣4 m3=6N。
答:(1)王强同学所选橡皮泥的质量为0.3kg;
(2)橡皮泥对桌面产生的压强为3000Pa;
(3)王强同学造的船在水中最大排水时受到的浮力为6N。
本题为力学综合题,考查了密度公式、重力公式、压强公式、阿基米德原理的应用虽然知识点多、综合性强,但都属于基础,难度不大!
12.将U型管压强计的金属盒放在盛有某种液体的玻璃杯中。相关信息如图所示。(g取10N/kg)求:
(1)液体的密度。
(2)体积为60cm3的小球浸没在液体中受到的浮力。
【考点】8P:浮力大小的计算.【分析】(1)根据金属盒受到液体压强与U形管中两边水的压强差相等,由此根据p=ρgh计算液体的密度。
(2)由阿基米德原理计算小球浸没在液体中受到的浮力。
【解答】解:
(1)金属盒受到液体压强与U形管中两边水的压强差相等,
即:p金属盒=p压强计,
由p=ρgh可得:
ρ液gh液=ρ水gh水,
所以液体密度:
ρ液=•ρ水=×1×103kg/m3=0.8×103kg/m3;
(2)小球浸没在液体中V排=V球=60cm3,
由阿基米德原理可得小球受到的浮力:
F浮=ρ液gV排=0.8×103kg/m3×10N/kg×60×10﹣6m3=0.48N。
答:(1)液体的密度为0.8×103kg/m3。
(2)小球浸没在液体中受到的浮力为0.48N。
本题考查了液体压强和浮力计算公式的应用,关键知道压强计算的原理。
13.如图是湖南师范大学学生发明的水上自行车,车下固定5个充满气的气囊,每个气囊的体积均为3.0×10﹣2m3,已知该水上自行车的总质量为25kg,不计车轮浸入水中的体积。(g取10N/kg)
(1)当自行车停放在水面上没人骑行时,气囊排开水的总体积为多少?
(2)当质量为75kg的人骑行时,固定在正中间的1个气囊破裂,该自行车是否还能安全骑行?请通过计算说明。
【考点】8O:阿基米德原理的应用;8S:物体的浮沉条件及其应用.【分析】(1)当自行车停放在水面上没人骑行时处于漂浮状态,受到的浮力和自身的重力相等,根据F浮=G=mg求出浮力的大小,根据阿基米德原理求出气囊排开水的总体积;
(2)当质量为75kg的人骑行恰好漂浮时受到的浮力等于自行车和人的重力之和,根据阿基米德原理求出排开水的体积,然后与气囊的总体积相比较得出答案。
【解答】解:(1)当自行车停放在水面上没人骑行时处于漂浮状态,
则自行车受到的浮力:
F浮=G车=m车g=25kg×10N/kg=250N,
由F浮=ρgV排可得,气囊排开水的总体积:
V排===0.025m3;
(2)当质量为75kg的人骑行恰好漂浮时,
则受到的浮力:
F浮′=G总=(m人+m车)g=(75kg+25kg)×10N/kg=1000N,
排开水的体积:
V排′===0.1m3,
剩余气囊的总体积:
V=4×3.0×10﹣2m3=0.12m3,
因V排′<V,
所以,该自行车能安全骑行。
答:(1)当自行车停放在水面上没人骑行时,气囊排开水的总体积为0.025m3;
(2)当质量为75kg的人骑行时,固定在正中间的1个气囊破裂,该自行车还能安全骑行。
本题考查了物体浮沉条件和阿基米德原理的应用,最后一问也可以求出剩余气囊所载物体的最大质量和人的质量相比较得出答案。
14.如图甲所示,石料在钢绳拉力的作用下从水面上方以恒定的速度下降,直至全部没入水中,如图乙所示是钢绳拉力随时间t变化的图象,若不计水的阻力(g=10N/kg,ρ水=1.0×103kg/m3),求:
(1)石料全部没入水中时受到的浮力是多少?
(2)石料的体积是多少?
(3)石料的密度是多少?
【考点】2A:密度的计算;8O:阿基米德原理的应用;8P:浮力大小的计算.【分析】(1)分析钢绳拉力随时间t变化的图象,石料以恒定的速度下降,当石块没有浸入水中时,拉力等于重力,据此求出小石料的质量;当石块完全浸入后,浮力等于重力减去拉力,据此求出石料受到的浮力;
(2)根据阿基米德原理求石料排开水的体积(石料的体积);
(3)知道石料重,利用重力公式求石料的质量,最后利用密度公式求石料的密度。
【解答】解:(1)由图乙所示图形学可知,
当石块没有浸入水中时,拉力等于重力,即:F=G=1400N,
石料的质量:
m石===140kg,
当石块完全浸入后,拉力等于重力减去浮力,
F浮=G﹣F′=1400N﹣900N=500N;
(2)根据阿基米德原理,F浮=ρ水gV排,得:
V排===5×10﹣2m3,
因为石料完全浸没,石料的体积:
V石=V排=5×10﹣2m3;
(3)石料的密度:
ρ石===2.8×103kg∕m3。
答:(1)石料浸没水中时受到的浮力为500N;
(2)石料的体积为5×10﹣2m3;
(3)石料的密度是2.8×103kg∕m3。
解决本题的关键是通过图乙确定石料的重力及钢丝绳受到的拉力,并会利用称重法计算出石料受到的浮力。
15.为增加学生的国防知识,某中学九(7)班同学到东海舰队参观某型号潜水艇。潜水艇的艇壳是用高强度的特种钢板制造,最大下潜深度可达350m。潜水艇的总体积为1.5×103m3,艇内两侧有水舱,潜水艇截面如图所示。通过向水舱中充水或从水舱中向外排水来改变潜水艇的自重,从而使其下沉或上浮。(海水密度为1.03×103kg/m3,g取10N/kg)
(1)水舱未充海水时,潜水艇总重力为9.27×106N,此时,漂浮在海面的潜水艇排开海水的体积是多少?
(2)为使潜水艇完全潜入水中,至少应向水舱充入海水的重力是多少?
(3)潜水艇的艇壳用高强度的特种钢板制造的原因是什么?
【考点】88:液体的压强的特点;8O:阿基米德原理的应用;8S:物体的浮沉条件及其应用.【分析】(1)潜水艇漂浮时浮力等于重力,求出浮力,利用阿基米德原理可求排开水的体积;
(2)已知潜艇的总体积可求潜水艇完全没入时受到的浮力,而潜水艇受到的浮力等于潜水艇重加上水舱内的水重,据此求出应向水舱充入海水的重;
(3)液体内部的压强随深度的增大而增大。
【解答】解:(1)∵潜水艇漂浮,
∴F浮=G=9.27×106N
∵F浮=ρ海水gV排,
∴潜水艇排开海水的体积:
V排===900m3;
(2)潜水艇没在水中时
F浮′=ρ海水gV排′=1.03×103kg/m3×10N/kg×1.5×103m3=1.545×107N,
F浮′=G艇+G海水
G海水=F浮′﹣G艇=1.545×107N﹣9.27×106N=6.18×106N;
(3)∵液体内部的压强随深度的增大而增大,
∴为了使潜水艇在深水处能承受更大的水压,艇壳用高强度的特种钢板制造。
答:(1)漂浮在海面的潜水艇排开海水的体积是900m3;
(2)为使潜水艇完全潜入海水中,至少应向水舱充入海水的重力是6.18×106N;
(3)潜水艇的艇壳用高强度的特种钢板制造的原因是为了使潜水艇在深水处能承受更大的水压。
本题考查了学生对液体压强公式、阿基米德原理、物体的漂浮条件的掌握和运用,要求灵活运用公式进行计算。
16.一个体积为80cm3的物块,漂浮在水面上时,有36cm3的体积露出水面,试问:
(l)物块所受浮力为多少?
(2)物块的密度为多少?(ρ水=1.0×103kg/m3,g=10N/kg)
【考点】2A:密度的计算;8O:阿基米德原理的应用.【分析】(1)根据题中条件,求出物块排开水的体积,即浸入水的体积,然后根据阿基米德原理F浮=G排=ρ液gV排求出物块受到的浮力;
(2)根据物块在水中是漂浮,可知物块的重力等于浮力。然后根据m=可求出其质量,再利用ρ=即可求出此物块的密度。
【解答】解:设物块的质量为m,体积为V1,露出水面上的体积为V2,
(1)F浮=ρ水g(V1﹣V2)=1.0×103kg/m3×10N/kg×(80﹣36)×10﹣6m3=0.44N。
答:物块所受浮力为0.44N。
(2)漂浮时物块的重力等于浮力,则G=F浮=0.44N,
则物块的质量m===0.044kg,
物块的密度ρ===0.55×103kg/m3。
答:物块的密度为0.55×103kg/m3。
该题考查了阿基米德原理的应用,掌握浮力计算公式是解答此题的关键,难易程度适中,计算时要注意单位的统一。
1
人教版八年级物理期末复习 第10章 浮力 计算题专练
1.伟大的中华民族正在走向复兴,人民海军走向深蓝。2019年4月23日,为庆祝中国人民海军成立七十周年,中国完全自主研制的055大型驱逐舰首次在山东青岛公开亮相。该舰是中国第一款排水量超过万吨的主力驱逐舰,舰长183m、宽23m,满载时吃水深度为8m,排水量可达12500t。(g取10N/kg,海水密度取ρ海水=1.0×103kg/m3)
(1)求055驱逐舰满载时所受的浮力;
(2)若一架总质量为13t的直升机为了执行侦察任务飞离驱逐舰,求055驱逐舰浸在水里的体积减少了多少。
【考点】8O:阿基米德原理的应用;8S:物体的浮沉条件及其应用.【分析】(1)知道055驱逐舰满载时的排水量,根据F浮=G排=m排g求出所受的浮力;
(2)直升机飞离驱逐舰前后驱逐舰始终漂浮,受到的浮力和自身的重力相等,据此求出直升机飞离驱逐舰后所受浮力的减少量,根据F浮=ρgV排求出055驱逐舰浸在水里的体积减少的量。
【解答】解:
(1)由阿基米德原理可得,055驱逐舰满载时所受的浮力:
F浮=G排=m排g=12500×103kg×10N/kg=1.25×108N;
(2)因直升机飞离驱逐舰前后驱逐舰始终漂浮,受到的浮力和自身的重力相等,
所以,直升机飞离驱逐舰后所受浮力的减少量:
△F浮=G=mg=13×103kg×10N/kg=1.3×105N,
由F浮=ρgV排可得,055驱逐舰浸在水里的体积减少了:
△V排===13m3。
答:(1)055驱逐舰满载时所受的浮力为1.25×108N;
(2)055驱逐舰浸在水里的体积减少了13m3。
本题考查了阿基米德原理和物体浮沉条件的应用,要注意直升机飞离驱逐舰前后驱逐舰所受浮力的变化等于直升机的重力。
2.如图所示,水平桌面上有一个薄壁溢水杯,底面积是8×10﹣3m2,装满水后水深0.1m,总质量是0.95kg。把一个木块(不吸水)轻轻放入水中,待木块静止时,从杯中溢出水的质量是0.1kg。求:(水的密度ρ=1.0×103kg/m3,g取10N/kg)
(1)水对溢水杯底的压力。
(2)木块受到的浮力。
(3)溢水杯对桌面的压力。
【分析】(1)知道水深,利用求p=ρgh水对溢水杯底的压强,再利用F=pS求水对溢水杯底的压力;
(2)根据阿基米德原理求木块所受的浮力;
(3)因为木块漂浮在水面上,所以F浮=G排=G木,溢水杯对桌面的压力等于原来溢水杯和水的总重力加上木块的重力再减去排开水的重力。
【解答】解:
(1)水对溢水杯底的压强:
p=ρgh=1.0×103kg/m3×10N/kg×0.1m=1000Pa,
由p=可得水对溢水杯底的压力:
F=pS=1000Pa×8×10﹣3m2=8N;
(2)由阿基米德原理可得木块所受的浮力:
F浮=G排=m排g=m溢g=0.1kg×10N/kg=1N;
(3)因为木块漂浮在水面上,所以F浮=G排=G木,
所以此时溢水杯对桌面的压力:
F=G+G木﹣G排=G=mg=0.95kg×10N/kg=9.5N。
答:(1)水对溢水杯底的压力为8N;
(2)木块受到的浮力为1N;
(3)溢水杯对桌面的压力为9.5N。
本题考查了重力公式、压强定义式、液体压强公式、阿基米德原理、物体漂浮条件的应用,要明确装满水的溢水杯在放入木块前后对桌面的压力相同。
3.某型号一次性声呐,其内部有两个相同的空腔,每个空腔的容积为2×10﹣3m3,每个空腔的侧上方都用轻薄易腐蚀材料制成的密封盖密封,密封盖在海水中浸泡24小时后,将被海水完全腐蚀。
某次公海军事演习,反潜飞机向海中投入该声呐,声呐在海中静止后露出整个体积的,声呐处于探测状态,如图甲所示,24小时后,声呐没入海中处于悬浮状态,声呐停止工作,如图乙所示,再经过24小时后,声呐沉入海底,如图丙所示。已知ρ海水=1.1×103kg/m3,g取10N/kg,问:
(1)每个空腔能容纳海水的重量有多大?
(2)声呐整个体积有多大?
(3)图甲中,声呐有多重?
(4)图丙中,海底对声呐的支持力有多大?
【考点】8O:阿基米德原理的应用;8S:物体的浮沉条件及其应用.【分析】(1)知道空腔的容积,由G=mg=ρVg求所容纳的海水的重力;
(2)在把声呐当作一个整体,这个整体包括两个空腔和其余部分,没有海水进入时,这个整体包含两个空腔;海水进入后,这个整体包括进入空腔的海水,图甲中,声呐漂浮,所受的浮力与重力相等,根据图乙所示,声呐在海水中悬浮,此时下方的密封盖被海水腐蚀,所受的浮力等于声呐自身重力和第一个空腔内的海水重力之和,据此解题;
(3)图甲中,声呐漂浮且有体积露出水面,由F浮=G求解;
(4)图丙中,计算此时声呐的总重力,由F支=G﹣F浮求解。
【解答】解:
(1)由题知,每个空腔的容积为V=2×10﹣3m3,
每个空腔能容纳海水的重量:
G海水=m海水g=ρ海水V腔g=1.1×103kg/m3×2×10﹣3m3×10N/kg=22N;
(2)设声呐的整个体积为V,声呐的重力为G声,
图甲中,声呐漂浮(下方的密封盖浸在海水中),且声呐在海中静止后露出整个体积的,
则:G声=F浮=ρ海水g(1﹣)V=ρ海水gV﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①,
图乙中,24小时后,下方的密封口被腐蚀,下方空腔充满海水,声呐悬浮,把声呐和进入的海水作为一个整体(即此时下方空腔内的海水作为声呐的一部分);
则由悬浮条件可得:F浮1=G总1=G声+G海水=ρ海水gV+22N﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②,
而此时声呐浸没在海水中,所以F浮1=ρ海水gV﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣③,
可得:ρ海水gV=ρ海水gV+22N,
解得:V=8×10﹣3m3;
(3)图甲中,声呐漂浮且有体积露出水面,
G声=F浮=ρ海水g(1﹣)V=×1.1×103kg/m3×10N/kg×8×10﹣3m3=66N;
(4)图丙中,声呐上方的密封盖也浸没在海水中,再经过24小时,密封盖也被腐蚀,把声呐和进入的海水作为一个整体(即此时两个空腔内的海水作为声呐的一部分);
则可知声呐的总重力:
G总2=G声+2×G海水=66N+2×22N=110N,
声呐受到的浮力:F浮1=ρ海水gV=1.1×103kg/m3×10N/kg×8×10﹣3m3=88N,
海底对声呐的支持力:F支=G总2﹣F浮1=110N﹣88N=22N。
答:(1)每个空腔能容纳海水的重量有22N;
(2)声呐整个体积为8×10﹣3m3;
(3)图甲中,声呐的重力为66N;
(4)图丙中,海底对声呐的支持力为22N。
本题考查阿基米德原理和物体的漂浮特点的应用,综合性强,难度较大。
4.学习了密度和浮力的相关知识后,某学校综合实践活动小组利用弹簧测力计、合金块、细线、已知密度的多种液体、笔、纸等,设计改装成一支密度计。他们的做法是:在弹簧测力计下面挂一个大小适度的合金块,分别将合金块完全浸没在水和煤油中,静止时弹簧测力计示数如图所示,在弹簧测力计刻度盘上标上密度值。再将合金块分别完全浸没在不同的校验液体中,重复上述操作,反复校对检验。这样就制成一支测定液体密度的“密度计”。(g=10N/kg,ρ煤油=0.8×103kg/m3)
(1)求合金块的密度。
(2)利用学过的公式原理,从理论上分析推导说明,待测液体的密度和弹簧测力计的示数的关系式,指出改装的密度计刻度是否均匀?改装后密度计的分度值是多少?决定密度计量程大小的关键因素是什么?
(3)计算说明密度为2.0×103kg/m3的刻度应该标在弹簧测力计的哪个位置?
【考点】8O:阿基米德原理的应用.【分析】(1)根据称重法测浮力F=G﹣F浮和阿基米德原理求出物体的体积和G,根据ρ=求出合金块的密度;
(2)由上得出:F示=4N﹣ρ液×10N/kg×10﹣4 m3;据此得出待测液体的密度和弹簧测力计的示数的关系:
分析这个关系式确定密度计刻度是均匀的;
由这个关系式,当最示数最大和最小时得出液体密度,从而得出改装后密度计的分度值;
由关系式,决定密度计量程大小的关键因素;
(3)把ρ液=2.0×103kg/m3代入关系式得了密度为2.0×103kg/m3的刻度应该标在弹簧测力计的位置。
【解答】解:(1)根据称重法测浮力F=G﹣F浮和阿基米德原理有:
3.0N=G﹣ρ水gV=G﹣1.0×103kg/m3×10N/kg×V﹣﹣﹣﹣①
3.2N=G﹣ρ煤油gV=G﹣0.8×103kg/m3×10N/kg×V﹣﹣﹣﹣②;
由①②得:V=10﹣4 m3;G=4N,
合金块的密度:
ρ===4×103kg/m3;
(2)由②得:F示=4N﹣ρ液×10N/kg×10﹣4 m3;
故待测液体的密度和弹簧测力计的示数的关系:
ρ液=4×103kg/m3﹣F示×103 kg/(N•m3)﹣﹣﹣﹣﹣﹣③,
由③知,
ρ液与F示为一次函数关系,改装的密度计刻度是均匀的;
由③知,当F示=4N时,ρ液=0;
当F示=0时,ρ液=4×103kg/m3;0﹣4N之间有20个格,
改装后密度计的分度值为:
=0.2×103kg/m3;
由③知,决定密度计量程大小的关键因素是合金块的密度;
(3)把ρ液=2.0×103kg/m3代入③得:F示=2.0N,即密度为2.0×103kg/m3的刻度应该标在弹簧测力计的2.0N位置处。
答:(1)合金块的密度为4×103kg/m3;
(2)待测液体的密度和弹簧测力计的示数的关系式为ρ液=4×103kg/m3﹣F示×103 kg/(N•m3),改装的密度计刻度是均匀的;改装后密度计的分度值是=0.2×103kg/m3;决定密度计量程大小的关键因素是合金块的密度;
(3)计算说明密度为2.0×103kg/m3的刻度应该标在弹簧测力计2N的位置。
本题制作一支测定液体密度的“密度计”,考查称重法测浮力、阿基米德原理、密度公式的运用和数据分析,关键是得出测液体的密度和弹簧测力计的示数的关系,有一定难度。
5.某容器放在水平桌面上,盛有足量的水。现将体积为1.25×10﹣4m3、质量为0.4kg的实心正方体放入水中,正方体不断下沉,直到沉底,如图所示。(已知ρ水=1.0×103kg/m3,g=10N/kg)求:
(1)正方体受到的重力的大小;
(2)正方体浸没在水中受到的浮力的大小F浮;
(3)容器底部对正方体的支持力的大小和正方体对容器底部的压强。
【考点】78:重力的计算;86:压强的大小及其计算;8O:阿基米德原理的应用.【分析】(1)知道正方体的质量,利用G=mg即可求出正方体的重力;
(2)正方体浸没在水中,排开水的体积与正方体的体积相等,根据F浮=ρ水gV排求出受到的浮力;
(3)正方体沉在底部,根据重力和浮力利用力的平衡即可求出支持力;
根据力的相互作用可知正方体对容器底部的压力,利用p=计算正方体对容器底部的压强。
【解答】解:(1)正方体的重力G=mg=0.4kg×10N/kg=4N;
(2)正方体浸没在水中,V排=V=1.25×10﹣4m3,
则F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1.25×10﹣4m3=1.25N;
(3)正方体沉在底部,由于处于静止状态,则受力平衡,即G=N+F浮,
所以,N=G﹣F浮=4N﹣1.25N=2.75N;
由于支持力与压力是一对相互作用力,则可知正方体对容器底部的压力F=N=2.75N,
正方体的边长L===0.05m,
则正方体对容器底部的压强p===1.1×103Pa。
答:(1)正方体受到的重力的大小为4N;
(2)正方体浸没在水中受到的浮力的大小F浮=1.25N;
(3)容器底部对正方体的支持力的大小为2.75N,正方体对容器底部的压强为1.1×103Pa。
此题考查浮力和液体压强的计算,关键是浮力公式、液体压强公式和压强定义式的应用,此题难度适中,适合学生训练,是一道好题。
6.2018年5月13日,中国首艘国产航母001A型航空母舰离开大连港码头,开始海试。(ρ水=1.0×103kg/m3,g取10N/kg)请问:
(1)航母001A设计排水量6.7×104t,那么它满载时受到的浮力是多少?
(2)海面下8m处的压强是多少?
(3)一位体重为600N的歼15舰载机飞行员,每只脚与水平甲板的接触面积是200cm2,则他双脚站立时对甲板的压强是多少?
【考点】86:压强的大小及其计算;89:液体的压强的计算;8P:浮力大小的计算.【分析】(1)物体所受浮力大小等于它排开液体所受重力;
(2)根据液体压强公式p=ρgh计算;
(3)根据p=计算;
【解答】解:
(1)根据阿基米德原理可得,该航母满载时受到的浮力:
F浮=G排=m排g=6.7×104×103kg×10N/kg=6.7×108N;
(2)海面下8m处的压强:
p=ρgh=1.0×103kg/m3×10N/kg×8m=8×104Pa;
(3)飞行员每只脚与水平甲板的接触面积是200cm2,
所以飞行员双脚站立的受力面积:S=2×200×10﹣4m2=4×10﹣2m2,
飞行员站立在水平甲板上,对甲板的压力F=G,
站立时对甲板的压强:p====1.5×104Pa;
答:(1)满载时受到的浮力是6.7×108N;
(2)海面下8m处的压强是8×104Pa;
(3)双脚站立时对甲板的压强是1.5×104Pa。
本题考查浮力和压强的知识,关键是将课本知识内容记忆清楚,仔细分析即可。
7.用弹簧测力计悬挂一实心物块,物块下表面与水面刚好接触,如图甲所示。由此处匀速下放物块,直至浸没于水中并继续匀速下放(物块始终未与容器接触)。物块下放过程中,弹簧测力计示数F与物块下表面浸入水中的深度h的关系如图乙所示。求:
(1)物块完全浸没在水中受到的浮力;
(2)物块的密度;
(3)从物块刚好浸没水中到h=10cm过程中,水对物块下表面的压强变化了多少Pa?
【考点】2A:密度的计算;89:液体的压强的计算;8O:阿基米德原理的应用;8P:浮力大小的计算.【分析】(1)由图象可知,弹簧测力计的最大示数,此时物块未浸入水中,物块重力等于最大示数;由图得出物块全浸入时弹簧测力计的示数,利用称重法求受到的浮力;
(2)利用F浮=ρ液V排g求物体的体积,利用G=mg求物体的质量,利用密度公式求物体的密度;
(3)由图乙可知,h1=4cm时物块刚好浸没水中,可求从物块刚好浸没水中到h2=10cm过程中物块下表面变化的深度,利用p=ρgh求水对物块下表面的压强变化。
【解答】解:
(1)由图象可知,弹簧测力计的最大示数F最大=8N,此时物块未浸入水中,则物块重力G=F最大=8N;
物块全浸入时弹簧测力计的示数F示=4N,
受到的浮力:
F浮=G﹣F示=8N﹣4N=4N;
(2)由F浮=ρ水gV排得物块的体积:
V=V排===4×10﹣4m3,
物块的质量:
m===0.8kg,
ρ物===2×103kg/m3;
(3)由图乙可知,h1=4cm时物块刚好浸没水中,从物块刚好浸没水中到h2=10cm过程中,
物块下表面变化的深度△h=h2﹣h1=10cm﹣4cm=6cm=0.06m,
水对物块下表面的压强变化:
△p=ρ水g△h=1×103kg/m3×10N/kg×0.06m=600Pa。
故答案为:(1)物块完全浸没在水中受到的浮力为4N;
(2)物块的密度2×103kg/m3;
(3)从物块刚好浸没水中到h=10cm过程中,水对物块下表面的压强变化了600Pa。
本题考查了重力公式、密度公式、阿基米德原理、液体压强公式的应用,分析图象得出相关信息是关键。
8.将物块竖直挂在弹簧测力计下,在空气中静止时弹簧测力计的示数F1=2.6N.将物块的一部分浸在水中,静止时弹簧测力计的示数F2=1.8N,如图所示,已知水的密度ρ=1.0×103kg/m3,g取10N/kg。
求:(1)物块受到的浮力;
(2)物块浸在水中的体积。
【考点】8O:阿基米德原理的应用;8P:浮力大小的计算.【分析】(1)在空气中静止时弹簧测力计的示数即为物块的重力,又知道物块的一部分浸在水中时弹簧测力计的示数,根据F浮=G﹣F′求出物块受到的浮力;
(2)根据阿基米德原理求出物块排开水的体积即为浸在水中的体积。
【解答】解:(1)由称重法可得物块受到的浮力:
F浮=F1﹣F2=2.6N﹣1.8N=0.8N;
(2)由F浮=ρ水gV排可得,物块浸在水中的体积:
V排===8×10﹣5m3。
答:(1)物块受到的浮力为0.8N;
(2)物块浸在水中的体积为8×10﹣5m3。
本题考查了称重法求浮力公式和阿基米德原理的应用,是一道较为简单的计算题。
9.如图甲所示,拉力F通过滑轮组,将正方体金属块从水中匀速拉出至水面上方一定高度处。图乙是拉力F随时间t变化的关系图象。不计动滑轮的重力、摩擦及水和空气对金属块的阻力,g=10N/kg,求:
(1)金属块完全浸没在水中时受到的浮力大小;
(2)金属块的密度;
(3)如果直接将金属块平放在水平地面上,它对地面的压强大小。
【考点】86:压强的大小及其计算;8P:浮力大小的计算.【分析】(1)当金属块完全露出液面,没有浸入水中时,金属块不受浮力,此时拉力等于重力,即为图中的CD段,据此求出金属块重。
分析绳子拉力随时间t变化的图象,当金属块从水中一直竖直向上做匀速直线运动,但未露出液面,此时金属块排开水的体积不变,由阿基米德原理可知,此时的浮力不变,绳子的拉力也不变。当金属块未露出液面时,拉力等于重力减去浮力,据此结合滑轮组绳子拉力的计算求出浮力大小;
(2)根据阿基米德原理求金属块排开水的体积(金属块的体积),知道金属块的重,利用重力和密度公式求金属块的密度。
(3)金属块平放在水平地面上,对地面的压力等于重力,利用体积公式求出金属块的边长,再利用面积公式求出金属块的底面积,即受力面积,最后利用压强公式计算压强。
【解答】解:
(1)由甲图可知,n=2,不计动滑轮的重力、摩擦及水和空气对金属块的阻力,F=G,
当金属块完全露出液面后,金属块不受浮力,此时拉力等于重力,即为图中的t2﹣t3时刻,
从乙图可知,该金属块重力为:G=2F=2×108N=216N,
当金属块未露出液面时,即为图中的0﹣t1时刻,
则2F′+F浮=G,
所以金属块完全浸没在水中时受到的浮力:F浮=G﹣2F′=216N﹣2×68N=80N;
(2)根据F浮=ρgV排可得,金属块排开水的体积:V排===8×10﹣3m3,
金属块完全浸没在水中,则金属块的体积V=V排=8×10﹣3m3,
则根据G=mg、ρ=可得,金属块的密度为:ρ金===2.7×103kg/m3。
(3)金属块的边长a===0.2m,
则受力面积S=a2=(0.2m)2=0.04m2,
金属块平放在水平地面时对地面的压强:p====5.4×103Pa。
答:(1)金属块完全浸没在水中时受到的浮力80N;
(2)金属块的密度2.7×103kg/m3;
(3)如果直接将金属块平放在水平地面上,它对地面的压强5.4×103Pa。
本题考查了重力、浮力、质量、密度、压强的计算以及阿基米德原理,关键是公式和公式变形的应用,难点是通过图乙确定金属块的重力及绳子受到的拉力、会用称重法计算出金属块受到的浮力。
10.工人师傅利用汽车作为动力,从水中打捞一个正方体物件,绳子通过定滑轮,一端系着物件,另一端拴在汽车上,如图甲所示。汽车拉着物件匀速上升,已知汽车对绳子的拉力F与物件底面距离水底的高度h的变化关系如图乙所示。绳子的体积、绳重及摩擦均忽略不计,g取l0N/kg。求:
(1)该物件的质量是多少?
(2)物件浸没在水中时,受到的浮力为多大?
(3)物件上表面恰好到达水面时,下表面受到水的压强为多少?
【考点】89:液体的压强的计算;8P:浮力大小的计算.【分析】(1)由图甲可知滑轮为定滑轮,则该物件离开水面后的拉力余该物件的重力相等,根据G=mg求质量;
(2)图甲中,滑轮为定滑轮,则在乙图中,拉力较小时且大小不变,说明物体浸没在液体中;5m﹣5.5m,拉力逐渐变大,说明物件在离开液体的过程中,正方体的棱长为0.5m;之后物体脱离液体,拉力与物体的重力相等;根据称重法即可求出物件浸没在水中时受到的浮力;
(3)物件上表面恰好到达水面时,根据乙图得出下表面所处的深度,根据压强公式p=ρgh即可求出下表面受到水的压强。
【解答】解:
(1)该物件离开水面后的拉力F2=2500N,由于图甲中,滑轮为定滑轮,则物体的重力为G=F2=2500N,
则物体质量:
m===250kg;
(2)由图乙知中,物体在水中时拉力F1=1250N;
根据称重法可知物件浸没在水中时受到的浮力:
F浮=G﹣F1=2500N﹣1250N=1250N;
(3)由图乙知中,物件上表面恰好到达水面时,下表面所处的深度为h=5.5m﹣5m=0.5m,
则下表面受到水的压强:
p=ρgh=1×103kg/m3×10N/kg×0.5m=5×103Pa。
答:(1)该物件的质量是250kg;
(2)物件浸没在水中时,受到的浮力为1250N;
(3)物件上表面恰好到达水面时,下表面受到水的压强为5×103Pa。
本题综合考查重力公式、定滑轮、称重法和液体压强公式的应用,关键是从图中获得有效的信息,难度较大。
11.某次物理活动举行了“造船”比赛,他们用的材料是密度为1.5×103kg/m3的橡皮泥,其中王强同学选了一块竖立在水平桌面上的圆柱体橡皮泥,它的底面积为1.0×10﹣3m2高为0.2m,最后造出了最大排水体积为6.0×10﹣4m3的小船。(ρ水=1.0×103kg/m3,g取10Nkg)求:
(1)王强同学所选橡皮泥的质量
(2)橡皮泥对桌面产生的压强。
(3)王强同学造的船在水中最大排水时受到的浮力。
【考点】2B:密度公式的应用;86:压强的大小及其计算;8O:阿基米德原理的应用.【分析】(1)根据V=Sh计算橡皮泥的体积,知道橡皮泥的体积和密度,利用m=ρV求橡皮泥的质量;
(2)利用G=mg求橡皮泥的重力;橡皮泥对桌面产生的压力等于其重力,知道受力面积,再利用p=求橡皮泥对桌面产生的压强;
(3)利用阿基米德原理求最大排水时受到的浮力。
【解答】解:
(1)由题知,圆柱体橡皮泥的底面积为1.0×10﹣3m2,高为0.2m,
则橡皮泥的体积:V=Sh=1.0×10﹣3m2×0.2m=2×10﹣4m3,
由ρ=得橡皮泥的质量:
m=ρV=1.5×103kg/m3×2×10﹣4m3=0.3kg;
(2)橡皮泥的重力:
G=mg=0.3kg×10N/kg=3N,
橡皮泥对桌面的压力:
F=G=3N,
受力面积S=1.0×10﹣3m2,
橡皮泥对桌面产生的压强:
p===3000Pa;
(3)该船在最大排水时受到的浮力:
F浮=ρ水gV排大=1.0×103kg/m3×10N/kg×6.0×10﹣4 m3=6N。
答:(1)王强同学所选橡皮泥的质量为0.3kg;
(2)橡皮泥对桌面产生的压强为3000Pa;
(3)王强同学造的船在水中最大排水时受到的浮力为6N。
本题为力学综合题,考查了密度公式、重力公式、压强公式、阿基米德原理的应用虽然知识点多、综合性强,但都属于基础,难度不大!
12.将U型管压强计的金属盒放在盛有某种液体的玻璃杯中。相关信息如图所示。(g取10N/kg)求:
(1)液体的密度。
(2)体积为60cm3的小球浸没在液体中受到的浮力。
【考点】8P:浮力大小的计算.【分析】(1)根据金属盒受到液体压强与U形管中两边水的压强差相等,由此根据p=ρgh计算液体的密度。
(2)由阿基米德原理计算小球浸没在液体中受到的浮力。
【解答】解:
(1)金属盒受到液体压强与U形管中两边水的压强差相等,
即:p金属盒=p压强计,
由p=ρgh可得:
ρ液gh液=ρ水gh水,
所以液体密度:
ρ液=•ρ水=×1×103kg/m3=0.8×103kg/m3;
(2)小球浸没在液体中V排=V球=60cm3,
由阿基米德原理可得小球受到的浮力:
F浮=ρ液gV排=0.8×103kg/m3×10N/kg×60×10﹣6m3=0.48N。
答:(1)液体的密度为0.8×103kg/m3。
(2)小球浸没在液体中受到的浮力为0.48N。
本题考查了液体压强和浮力计算公式的应用,关键知道压强计算的原理。
13.如图是湖南师范大学学生发明的水上自行车,车下固定5个充满气的气囊,每个气囊的体积均为3.0×10﹣2m3,已知该水上自行车的总质量为25kg,不计车轮浸入水中的体积。(g取10N/kg)
(1)当自行车停放在水面上没人骑行时,气囊排开水的总体积为多少?
(2)当质量为75kg的人骑行时,固定在正中间的1个气囊破裂,该自行车是否还能安全骑行?请通过计算说明。
【考点】8O:阿基米德原理的应用;8S:物体的浮沉条件及其应用.【分析】(1)当自行车停放在水面上没人骑行时处于漂浮状态,受到的浮力和自身的重力相等,根据F浮=G=mg求出浮力的大小,根据阿基米德原理求出气囊排开水的总体积;
(2)当质量为75kg的人骑行恰好漂浮时受到的浮力等于自行车和人的重力之和,根据阿基米德原理求出排开水的体积,然后与气囊的总体积相比较得出答案。
【解答】解:(1)当自行车停放在水面上没人骑行时处于漂浮状态,
则自行车受到的浮力:
F浮=G车=m车g=25kg×10N/kg=250N,
由F浮=ρgV排可得,气囊排开水的总体积:
V排===0.025m3;
(2)当质量为75kg的人骑行恰好漂浮时,
则受到的浮力:
F浮′=G总=(m人+m车)g=(75kg+25kg)×10N/kg=1000N,
排开水的体积:
V排′===0.1m3,
剩余气囊的总体积:
V=4×3.0×10﹣2m3=0.12m3,
因V排′<V,
所以,该自行车能安全骑行。
答:(1)当自行车停放在水面上没人骑行时,气囊排开水的总体积为0.025m3;
(2)当质量为75kg的人骑行时,固定在正中间的1个气囊破裂,该自行车还能安全骑行。
本题考查了物体浮沉条件和阿基米德原理的应用,最后一问也可以求出剩余气囊所载物体的最大质量和人的质量相比较得出答案。
14.如图甲所示,石料在钢绳拉力的作用下从水面上方以恒定的速度下降,直至全部没入水中,如图乙所示是钢绳拉力随时间t变化的图象,若不计水的阻力(g=10N/kg,ρ水=1.0×103kg/m3),求:
(1)石料全部没入水中时受到的浮力是多少?
(2)石料的体积是多少?
(3)石料的密度是多少?
【考点】2A:密度的计算;8O:阿基米德原理的应用;8P:浮力大小的计算.【分析】(1)分析钢绳拉力随时间t变化的图象,石料以恒定的速度下降,当石块没有浸入水中时,拉力等于重力,据此求出小石料的质量;当石块完全浸入后,浮力等于重力减去拉力,据此求出石料受到的浮力;
(2)根据阿基米德原理求石料排开水的体积(石料的体积);
(3)知道石料重,利用重力公式求石料的质量,最后利用密度公式求石料的密度。
【解答】解:(1)由图乙所示图形学可知,
当石块没有浸入水中时,拉力等于重力,即:F=G=1400N,
石料的质量:
m石===140kg,
当石块完全浸入后,拉力等于重力减去浮力,
F浮=G﹣F′=1400N﹣900N=500N;
(2)根据阿基米德原理,F浮=ρ水gV排,得:
V排===5×10﹣2m3,
因为石料完全浸没,石料的体积:
V石=V排=5×10﹣2m3;
(3)石料的密度:
ρ石===2.8×103kg∕m3。
答:(1)石料浸没水中时受到的浮力为500N;
(2)石料的体积为5×10﹣2m3;
(3)石料的密度是2.8×103kg∕m3。
解决本题的关键是通过图乙确定石料的重力及钢丝绳受到的拉力,并会利用称重法计算出石料受到的浮力。
15.为增加学生的国防知识,某中学九(7)班同学到东海舰队参观某型号潜水艇。潜水艇的艇壳是用高强度的特种钢板制造,最大下潜深度可达350m。潜水艇的总体积为1.5×103m3,艇内两侧有水舱,潜水艇截面如图所示。通过向水舱中充水或从水舱中向外排水来改变潜水艇的自重,从而使其下沉或上浮。(海水密度为1.03×103kg/m3,g取10N/kg)
(1)水舱未充海水时,潜水艇总重力为9.27×106N,此时,漂浮在海面的潜水艇排开海水的体积是多少?
(2)为使潜水艇完全潜入水中,至少应向水舱充入海水的重力是多少?
(3)潜水艇的艇壳用高强度的特种钢板制造的原因是什么?
【考点】88:液体的压强的特点;8O:阿基米德原理的应用;8S:物体的浮沉条件及其应用.【分析】(1)潜水艇漂浮时浮力等于重力,求出浮力,利用阿基米德原理可求排开水的体积;
(2)已知潜艇的总体积可求潜水艇完全没入时受到的浮力,而潜水艇受到的浮力等于潜水艇重加上水舱内的水重,据此求出应向水舱充入海水的重;
(3)液体内部的压强随深度的增大而增大。
【解答】解:(1)∵潜水艇漂浮,
∴F浮=G=9.27×106N
∵F浮=ρ海水gV排,
∴潜水艇排开海水的体积:
V排===900m3;
(2)潜水艇没在水中时
F浮′=ρ海水gV排′=1.03×103kg/m3×10N/kg×1.5×103m3=1.545×107N,
F浮′=G艇+G海水
G海水=F浮′﹣G艇=1.545×107N﹣9.27×106N=6.18×106N;
(3)∵液体内部的压强随深度的增大而增大,
∴为了使潜水艇在深水处能承受更大的水压,艇壳用高强度的特种钢板制造。
答:(1)漂浮在海面的潜水艇排开海水的体积是900m3;
(2)为使潜水艇完全潜入海水中,至少应向水舱充入海水的重力是6.18×106N;
(3)潜水艇的艇壳用高强度的特种钢板制造的原因是为了使潜水艇在深水处能承受更大的水压。
本题考查了学生对液体压强公式、阿基米德原理、物体的漂浮条件的掌握和运用,要求灵活运用公式进行计算。
16.一个体积为80cm3的物块,漂浮在水面上时,有36cm3的体积露出水面,试问:
(l)物块所受浮力为多少?
(2)物块的密度为多少?(ρ水=1.0×103kg/m3,g=10N/kg)
【考点】2A:密度的计算;8O:阿基米德原理的应用.【分析】(1)根据题中条件,求出物块排开水的体积,即浸入水的体积,然后根据阿基米德原理F浮=G排=ρ液gV排求出物块受到的浮力;
(2)根据物块在水中是漂浮,可知物块的重力等于浮力。然后根据m=可求出其质量,再利用ρ=即可求出此物块的密度。
【解答】解:设物块的质量为m,体积为V1,露出水面上的体积为V2,
(1)F浮=ρ水g(V1﹣V2)=1.0×103kg/m3×10N/kg×(80﹣36)×10﹣6m3=0.44N。
答:物块所受浮力为0.44N。
(2)漂浮时物块的重力等于浮力,则G=F浮=0.44N,
则物块的质量m===0.044kg,
物块的密度ρ===0.55×103kg/m3。
答:物块的密度为0.55×103kg/m3。
该题考查了阿基米德原理的应用,掌握浮力计算公式是解答此题的关键,难易程度适中,计算时要注意单位的统一。
1
相关资料
更多








