热点09 立体几何中的平行关系与垂直关系（7 题型 高分技法 限时提升练）-2025年高考数学 热点 重点 难点 专练（天津专用）

这是一份热点09 立体几何中的平行关系与垂直关系（7 题型 高分技法 限时提升练）-2025年高考数学 热点 重点 难点 专练（天津专用），文件包含热点09立体几何中的平行关系与垂直关系7题型高分技法限时提升练-2025年高考数学热点重点难点专练天津专用原卷版docx、热点09立体几何中的平行关系与垂直关系7题型高分技法限时提升练-2025年高考数学热点重点难点专练天津专用解析版docx等2份试卷配套教学资源，其中试卷共58页， 欢迎下载使用。

题型1 空间中线，面平行，垂直关系的判断
1．（2022·天津北辰·模拟预测）设为两两不重合的平面，为两两不重合的直线，给出下列命题：
①若，则；
②若，，则；
③若，，则；
其中真命题的个数是（ ）
A．1B．2C．3D．0
2．（24-25高三上·天津河北·期末）已知，是两个平面，l，m是两条不同的直线，则下列说法正确的是（ ）
A．若，，则B．若，，则
C．若，，则D．若，，则
3．（24-25高三上·天津北辰·期末）已知是空间中的两个不同的平面，l，m，n是三条不同的直线.下列命题正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
4．（24-25高三上·天津和平·期末）已知，为两条不同的直线，，为两个不同的平面，则下列说法中正确的是（ ）
A．若，，则B．若，，则
C．若，，则D．若，，则
5．（24-25高三上·天津河西·期末）设是两条不同的直线，是两个不同的平面，则下列说法中正确的是（ ）
A．若，则
B．若，则
C．若，则
D．若，则
题型2线面平行证明
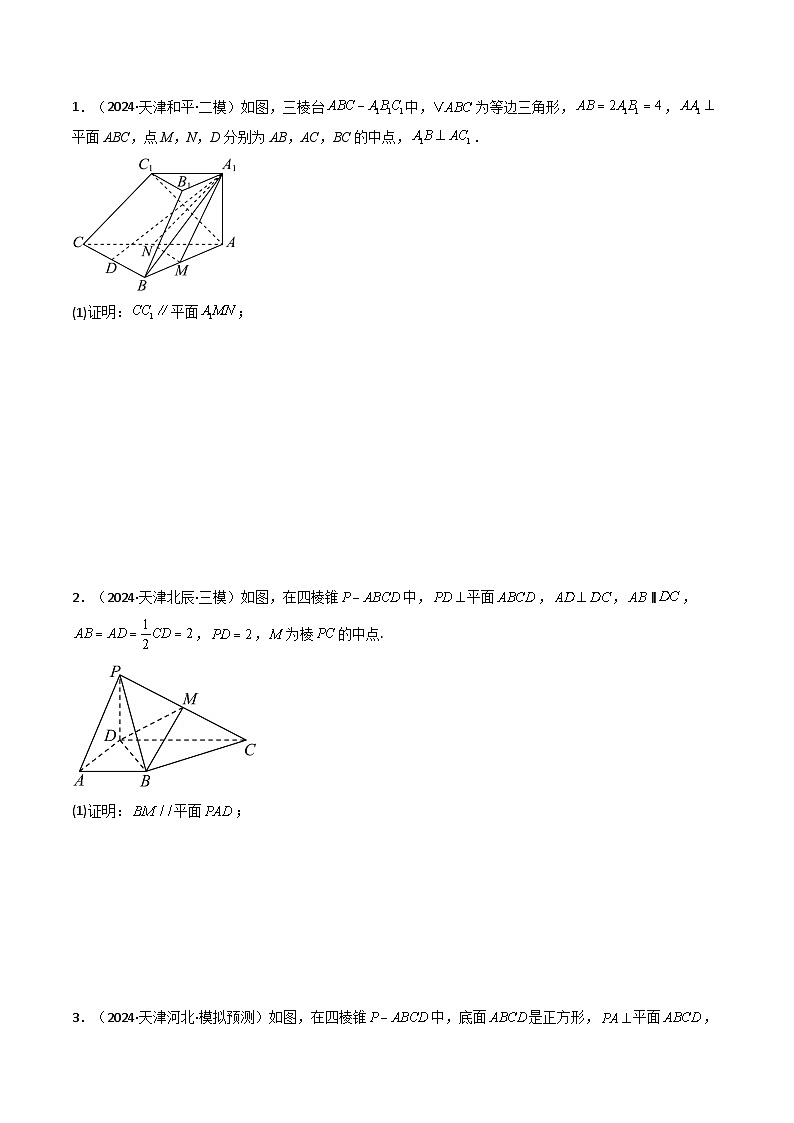
1．（2024·天津和平·二模）如图，三棱台中，为等边三角形，，平面ABC，点M，N，D分别为AB，AC，BC的中点，．
(1)证明：平面；
2．（2024·天津北辰·三模）如图，在四棱锥中，平面，，∥，，，为棱的中点.
(1)证明：平面；
3．（2024·天津河北·模拟预测）如图，在四棱锥中，底面是正方形，平面，，，分别是，的中点．
(1)求证：平面；
4．（2024·天津·二模）如图，直线垂直于梯形所在的平面，，为线段上一点，，四边形为矩形.

(1)若是的中点，求证：平面；
5．（2024·天津红桥·二模）在如图所示的几何体中，平面，，四边形为平行四边形，，，，．
求证：直线平面；
题型3线线平行证明
1．（2024·北京海淀·三模）如图，在四棱锥中，直线平面PCD，，，，平面平面ABCD，F为线段BC的中点，E为线段PF上一点．
(1)证明：；
2．（2024·陕西西安·一模）图1所示的是等腰梯形ABCD，AB//CD，AB=3，CD=1，，DE⊥AB于E点，现将△ADE沿直线DE折起到△PDE的位置，连接PB，PC，形成一个四棱锥P-EBCD，如图2所示．
(1)若平面PCD∩平面PBE=l，求证：DC//l；
3．（2024·河北保定·三模）如图，在四棱锥中，四边形为正方形，平面，且.E，F分别是PA，PD的中点，平面与PB，PC分别交于M，N两点.
(1)证明：；
4．（2024·江苏·模拟预测）如图，在四棱台中，，，．
(1)记平面与平面的交线为，证明：；
5．（2024·北京·三模）如图，在四棱锥中，底面是边长为2的菱形，，，为中点，．
设平面平面，求证：；
题型4 面面平行证明
1．（2024·甘肃白银·一模）如图，在四棱台中，底面和均为正方形，平面平面为线段上一点.
(1)若为线段的中点，证明：平面平面.
2．（2024·黑龙江·模拟预测）已知正三棱柱中分别为的中点，.
(1)证明:平面平面;
3．（2024·黑龙江哈尔滨·模拟预测）如图，在三棱柱中，侧面为矩形，M，N分别为AC，的中点．
(1)求证：平面平面；
4．（2024·云南曲靖·模拟预测）如图，四面体的每条棱长都等于2，分别是棱的中点，分别为面，面，面的重心.
(1)求证：面面；
5．（2024·四川眉山·三模）如图，在多面体中，四边形为菱形，平面平面，平面平面是等腰直角三角形，且.
证明：平面平面；
题型5 线面垂直证明
1．（2024·江西新余·模拟预测）如图，在平面图形甲中，，，与分别为以斜边的等腰直角三角形，现将该图形沿向上翻折使边重合（重合于），连.图乙中，为中点.
(1)求证：平面；
(2)求证：平面；
2．（2024·海南省直辖县级单位·模拟预测）如图，在三棱柱中，四边形是菱形，、分别是、的中点，平面平面，，．
(1)证明：平面；
3．（2024·山东威海·一模）如图，在四棱锥中，平面平面为等边三角形，，为的中点.
(1)证明：平面；
4．（2024·广东·模拟预测）如图，在三棱柱中，侧面是边长为2的菱形，其对角线交于点.且平面.

(1)求证：平面；
5．（2024·广东河源·模拟预测）如图，四棱锥的底面为直角梯形，，，，，为等边三角形，平面平面，，为的中点．
证明：平面；
题型6 线线垂直证明
1．（24-25高三上·宁夏石嘴山·期中）如图，在三棱柱中，平面，，，，点，分别在棱和棱上，且，，为棱的中点．
(1)求证：；
2．（24-25高三上·黑龙江哈尔滨·期中）已知矩形中， ，，是的中点，如图所示，沿将翻折至，使得平面平面.

(1)证明：；
3．（2024·全国·模拟预测）如图，在三棱锥中，已知为锐角三角形，平面平面，，点是的中点．
(1)求证：；
4．（2024·全国·模拟预测）如图，在直四棱柱中，，．
(1)证明：；
5．（2024·浙江温州·一模）如图，在三棱柱中，平面平面，平面.
求证：；
题型7 面面垂直证明
1．（2024·山东淄博·一模）如图，多面体ABCDEF是由一个正四棱锥与一个三棱锥拼接而成，正四棱锥A-BCDE的所有棱长均为.
(1)在棱DE上找一点G，使得面面AFG，并给出证明;
2．（23-24高一下·天津滨海新·期末）如图，在棱长均为2的正三棱柱中，为棱的中点．

(1)求证：直线平面；
(2)求证：平面平面；
3．（23-24高一下·天津武清·阶段练习）已知四边形为直角梯形，，，为等腰直角三角形，平面平面，E为的中点，，．

(1)求证：平面；
(2)求证：平面平面．
4．（23-24高一下·天津静海·阶段练习）如图，在三棱柱中，四边形为菱形，，分别为的中点，．
(1)求证：平面平面；
5．（24-25高二上·上海·期末）如图，在长方体中，，点在棱上移动．
(1)当点在棱的中点时，证明：平面平面；
（建议用时：60分钟）
一、单选题
1．（24-25高三上·天津红桥·期中）设，是两个不同的平面，l是一条直线，下列命题是真命题的为（ ）
A．若，，则B．若，，则
C．若，，则D．若，，则
2．（24-25高二上·吉林长春·期中）已知是两个平面，是两条不同的直线，则下列说法正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
3．（23-24高一下·天津红桥·期末）设，是两条不同的直线，，，是三个不同的平面，则下列命题为真命题的是（ ）
A．若，，则，B．若，，则
C．若，，则D．若，，，则
4．（23-24高一下·天津滨海新·期末）已知是两个不同的平面，是两条不同的直线，则下列说法正确的是（ ）
A．若，则B．若m⊥α,n//α，则
C．若，则D．若，则
5．（23-24高一下·天津·期末）已知，是两条不同的直线，，是两个不同的平面，则下列命题中正确的是（ ）
A．若，，，则
B．若，，，则
C．若，，，则
D．若，，，则
二、填空题
6．（24-25高三上·天津东丽·阶段练习）已知，，是不同的平面，，，是不同的直线，下列命题中所有真命题的序号是
（1）若，，，则；（2）若，，，则且；
（3）若，，，则；（4）若，，，则.
三、解答题
7．（23-24高一下·天津·期末）如图，在正方体中，为的中点．
(1)求证：平面；
(2)求证：．
8．（23-24高二上·天津北辰·阶段练习）如图，四棱锥的底面是正方形，平面，分别是的中点，其中.

(1)求证：平面PDB；
(2)求证：平面PDB.
9．（23-24高一下·天津西青·期末）如图，直三棱柱中，，E、F分别为AB、的中点．
(1)求证：平面；
(2)求证：；
10．（23-24高一下·天津滨海新·阶段练习）如图，正方体的棱长为1，线段上有两个不同的动点.

(1)求证：平面；
(2)求证：；
11．（23-24高二下·天津河北·期末）如图，在正方体中，与交于，是的中点．
(1)求证：平面；
(2)求证：平面．
12．（23-24高一下·天津·期末）如图，在四棱锥中，平面平面，且，，，为AD的中点.
(1)求证：平面；
(2)求证：平面平面；
三年考情分析
2025考向预测
2022年，第17（1）题，考察线面平行
2023年，第17（1）题，考察线面平行
2024年，第6题，综合考察判断线面平行垂直关系
2024年 第17（1）题，考察线面平行
在天津高考数学中，本部分内容主要分两方面进行考查，一是以几何体为载体考查空间点、线、面位置关系的判断，主要以小题的形式出现，题目难度较小；二是空间线线、线面、面面平行和垂直关系的证明，属于简单档题。
常以选择题形式出现，可通过借助长方体模型，判断线线，线面，面面的平行或垂直关系
(1)直线与平面平行的判定定理
如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行
符号表述：
图形语言
直线与平面平行的性质定理
如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行
符号表述：，，
简记：线线平行 线面平行
两个平面平行的判定定理
如果一个平面内的有两条相交直线平行于另一个平面,那么这两个平面平行.（定理简述：线面平行，则面面平行。）
（2）符号语言
（3）图形语言
直线与平面垂直的判定定理
（1）直线与平面垂直的判定定理： 如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直. 简记：线线垂直线面垂直
（2）符号语言：，，，，
（3）图形语言：如图
直线与平面垂直的性质定理(定义)
（1）定义转化性质：如果一条直线与平面垂直，那么直线垂直于平面内所有直线.
（2）符合语言：，.
（3）图形语言：
（4）定理应用：线面垂直线线垂直.
平面与平面垂直的判定定理
（1）定理：如果一个平面过另一个平面的的垂线，那么这两个平面垂直.(线面垂直，则面面垂直)
（2）符号（图形）语言:，