专题2　数列【讲】-2025年高考数学大题精做讲练（题型破局）附答案解析

这是一份专题2　数列【讲】-2025年高考数学大题精做讲练（题型破局）附答案解析，共24页。

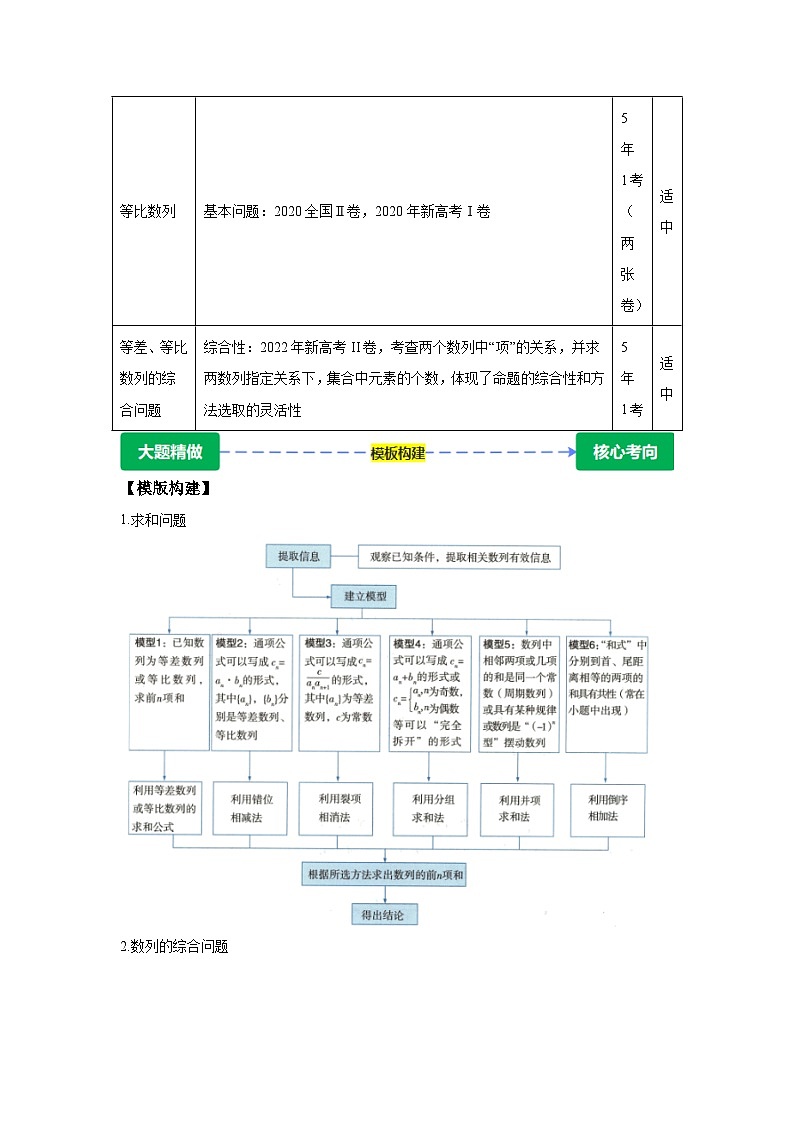
【模版构建】
1.求和问题
2.数列的综合问题
核心考向1 等差数列求和问题
【典例探究1】（2021年全国新高考I卷）已知数列满足，
（1）记，写出，，并求数列的通项公式；
（2）求的前20项和.
【思维建模】
【深度解析】
（1）[方法一]【最优解】：
显然为偶数，则，
所以，即，且，
所以是以2为首项，3为公差的等差数列，
于是．
[方法二]：奇偶分类讨论
由题意知，所以．
由（为奇数）及（为偶数）可知，
数列从第一项起，
若为奇数，则其后一项减去该项的差为1，
若为偶数，则其后一项减去该项的差为2．
所以，则．
[方法三]：累加法
由题意知数列满足．
所以，
，
则．
所以，数列的通项公式．
（2）[方法一]：奇偶分类讨论
．
[方法二]：分组求和
由题意知数列满足，
所以．
所以数列的奇数项是以1为首项，3为公差的等差数列；
同理，由知数列的偶数项是以2为首项，3为公差的等差数列．
从而数列的前20项和为：
．
【高分技法】
必备知识 如果数列的奇数项、偶数项构成等差或等比数列，则求其前n项和时可以使用分组求和方法，使具有相同结构的部分分别求和，然后将结果相加、化简即可
高分技法
数列求和必记4大技法结论
【典例探究2】（24-25高三上·黑龙江鸡西·阶段练习）已知数列的首项为，且满足.
(1)证明：数列为等差数列；
(2)求数列的前项和为；
(3)求数列的前项和.
【思维建模】
【深度解析】
（1）因为，，
若，则，与矛盾，
所以，所以，
所以，因为，所以，
所以数列是以首项为2，公差为4的等差数列.
（2）由（1）知，
数列的前项和为.
（3）因为，
设数列的前n项和为，
当n为偶数时，，
因为，
所以，
当为奇数时，为偶数.
，
所以.
核心考向2 等差数列求和与不等式证明问题
【典例探究3】（2023年新课标全国Ⅱ卷）已知为等差数列，，记，分别为数列，的前n项和，，．
(1)求的通项公式；
(2)证明：当时，．
【思维建模】
【深度解析】
（1）设等差数列的公差为，而，
则，
于是，解得，，
所以数列的通项公式是.
（2）方法1：由（1）知，，，
当为偶数时，，
，
当时，，因此，
当为奇数时，，
当时，，因此，
所以当时，.
方法2：由（1）知，，，
当为偶数时，，
当时，，因此，
当为奇数时，若，则
，显然满足上式，因此当为奇数时，，
当时，，因此，
所以当时，.
【典例探究4】已知数列的前n项和为，且，
（1）记，证明数列是等比数列，并求的通项公式．
（2）证明．
【思维建模】
【深度解析】
（1）由题意可知（【理思路】抓住等比数列的定义，根据“相邻两项之商为非零常数”将分子、分母往相同的项去凑，特别注意数列是分奇偶项的，从到，是代入奇数项的式子，从到，却要代入偶数项的式子，（3分）
所以数列是首项为，公比为6的等比数列．（4分）
由等比数列的定义可得．（5分）
（2）由题意可知，，
所以
；-（6分）
（【释疑难】这里进行重新分组，不再按照奇偶项，而是合并同类项，转化为求的和，第（1）问的条件“”给了我们这个暗示）（7分）
．（8分）
，令，（10分）
则，（12分）
所以数列是递增数列，故，即．（13分）
核心考向3 等差数列最值问题
【典例探究5】（2021年全国新高考II卷）记是公差不为0的等差数列的前n项和，若．
（1）求数列的通项公式；
（2）求使成立的n的最小值．
【思维建模】
【深度解析】
(1)由等差数列的性质可得：，则：，
设等差数列的公差为，从而有：，
，
从而：，由于公差不为零，故：，
数列的通项公式为：.
(2)由数列的通项公式可得：，则：，
则不等式即：，整理可得：，
解得：或，又为正整数，故的最小值为.
【典例探究6】（24-25高三上·内蒙古锡林郭勒盟·期中）记是公差不为的等差数列的前项和，若.
(1)求数列的通项公式；
(2)求使成立的的最大值.
【思维建模】
【深度解析】
（1）设等差数列的公差为，
由题知，解得，
所以.
（2）由（1）知，
所以，由，得到，整理得到，
解得，又，所以使成立的的最大值为.
核心考向4 等比数列基本问题
【典例探究7】（2020年新高考全国Ⅱ卷）已知公比大于的等比数列满足．
（1）求的通项公式；
（2）求.
【思维建模】
【深度解析】
(1) 设等比数列的公比为q(q>1)，则，
整理可得：，
，
数列的通项公式为：.
(2)由于：，故：
.
【典例探究8】已知数列满足，且．
(1)求的通项公式；
(2)设，且数列的前项和为，若，求的最大值．
【思维建模】
【深度解析】
（1）因为，所以，
故，又，则，
所以数列是首项为2，公比为2的等比数列，
所以，解得，
所以数列的通项公式为；【常用方法：取倒数，构造等比数列，利用等比数列通项公式】
（2）由（1）知，则，
所以
，
因为
恒成立，
所以是单调递增数列，
且，，
故使得的的最大值为3.
核心考向5 等差、等比数列综合问题
【典例探究9】（2022年新高考全国II卷）已知为等差数列，是公比为2的等比数列，且．
(1)证明：；
(2)求集合中元素个数．
【思维建模】
【深度解析】
（1）证明：设等差数列的公差为d．因为是公比为2的等比数列，
由得，即．（2分）
由得，即．（4分）
将代入，得，即．（5分）
（2）由（1）知，（7分）
由得，
由得，（8分）
由题知，所以，所以，3，4，…，10，共9个数，即集合中元素的个数为9．（10分）
【典例探究10】已知等差数列和等比数列满足，，，.
(1)求数列，的通项公式；
(2)设数列中不在数列中的项按从小到大的顺序构成数列，记数列的前项和为，求.
【思维建模】
【深度解析】
（1）设等差数列的公差为，
因为，所以，
所以，所以，
又，即，所以，所以.
（2）由（1）得，
即是数列中的第项.
设数列的前项和为，数列的前项和为，
因为，，
所以数列的前100项是由数列的前107项去掉数列的前7项后构成的，
所以.
（核心考向：等差数列求和问题）
1．已知数列的前项和，，，．
(1)计算的值，求的通项公式；
(2)设，求数列的前项和．
（核心考向：等差数列求和与不等式证明）（24-25高三上·陕西渭南·阶段练习）
2．记为数列的前n项和，已知是公差为的等差数列．
(1)求的通项公式；
(2)证明：．
（核心考向：等差数列、最值问题）
3．已知数列的前n项和满足，且．
(1)求数列的通项公式；
(2)记，为的前n项和，求使成立的n的最小值．
（核心考向：等比数列基本问题）（24-25高三上·黑龙江齐齐哈尔·期中）
4．已知数列满足.
(1)证明：数列是等比数列，并求数列的通项公式；
(2)设，求数列的前项和.
（核心考向：等差、等比数列的综合问题）（2024·吉林长春·模拟预测）
5．记是公差不为0的等差数列的前项和，，且，，成等比数列.
(1)求和；
(2)若，求数列的前20项和.
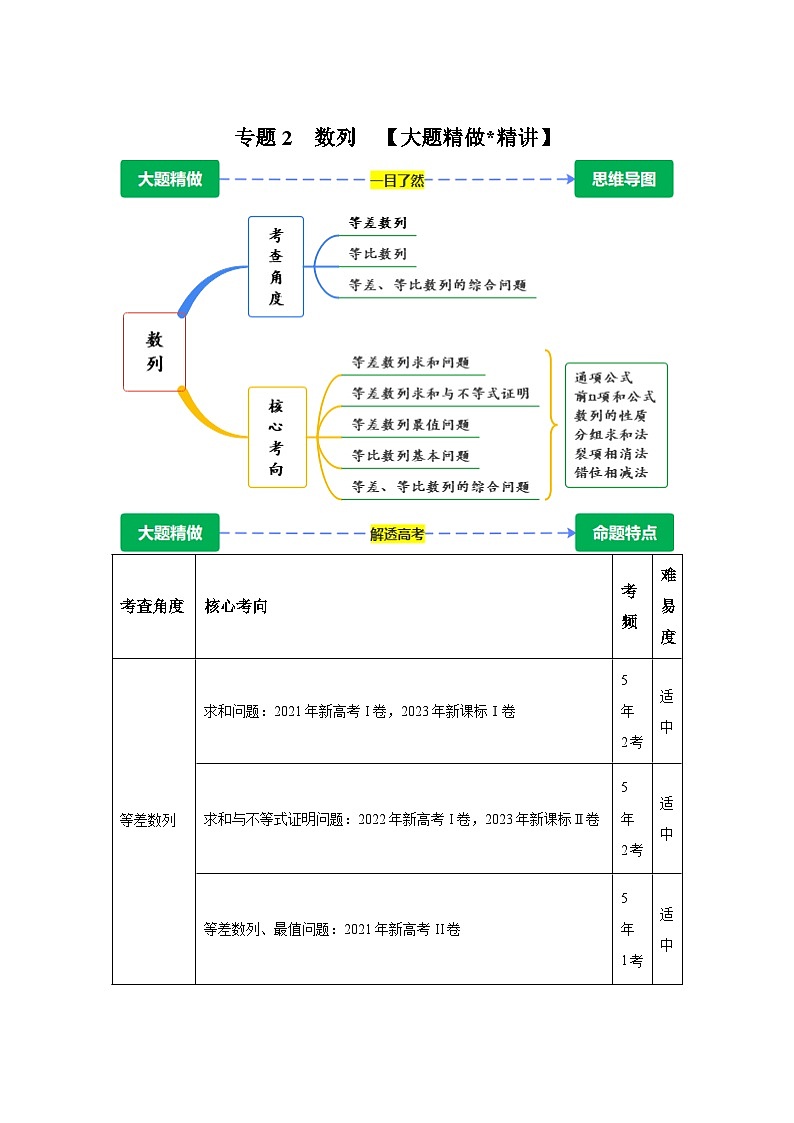
考查角度
核心考向
考频
难易度
等差数列
求和问题：2021年新高考I卷，2023年新课标Ⅰ卷
5年2考
适中
求和与不等式证明问题：2022年新高考I卷，2023年新课标Ⅱ卷
5年2考
适中
等差数列、最值问题：2021年新高考II卷
5年1考
适中
等比数列
基本问题：2020全国Ⅱ卷，2020年新高考Ⅰ卷
5年1考
（两张卷）
适中
等差、等比数列的综合问题
综合性：2022年新高考II卷，考查两个数列中“项”的关系，并求两数列指定关系下，集合中元素的个数，体现了命题的综合性和方法选取的灵活性
5年1考
适中
设问
已知量
模型应用
（1）求，，通项公式
，，
最优解：根据为偶数，有
可得，求得
（2）求前20项和
，
的通项公式
思路一：奇偶分类讨论．
思路二：分组求和
等差数列求和公式
①；②；③（其中，）
等比数列求和公式
①；②（，）；③（，）
经典数列求和公式
平方和公式：；
立方和公式：；
组合数求和公式：
9个常见裂项形式
①；
②（k为常数，）；
③（k为常数，）；
④；
⑤；
⑥；
⑦；
⑧，
⑨（）
设问
已知量
模型应用
（1）证明等差数列
，且满足.
递推数列变形+等差数列定义→证结
（2）求和
由（1）得
公式法求等差数列前项和，得
（3）求和
由（2）得
讨论n的奇数、偶数，分别求和
设问
已知量
模型应用
求的通项公式
，，．
已知是等差数列，通过布列方程组，可得其通项公式；应用公式求等差数列的和，的通项公式是分段的形式，需要分n为奇数和n为偶数两类求和
证明时，
设问
已知量
模型应用
（1）证明等比数列、求通项
结合分段数列的通项公式求→利用等比数列的定义证明→利用公式法求
（2）证明不等式成立
证明
将用的前n项和表示→重新分组求和→作差构造新数列→利用定义判断数列的单调性→得证
设问
已知量
模型应用
（1）求通项公式
等差数列的性质求得，利用另一条件求得公差，得解
（2）求使成立的n的最小值
，
由（1）得；求和，解不等式即，确定n的最小值.
设问
已知量
模型应用
（1）求通项公式
设公差d，根据条件→建立方程组→解方程组→
（2）求使不等式成立的的最大值
由（1）得
由（1）得，进而求和→解，即→，结合可得
设问
已知量
模型应用
（1）求通项公式
由题意得到关于首项、公比的方程组；解方程组得首项、公比；得到通项公式
（2）新数列和
由（1）得的通项公式，应用公式求和
设问
已知量
模型应用
（1）求通项公式
，且
取到数，构造，即得
（2）求的最大值
，且，的和
由（1）知，得到，分组求和，利用Sn知是单调递增
设问
已知量
模型应用
（1）证明
是等差数列，是公比为2的等比数列，且
研究的对象是两个首项，联系等差数列和等比数列通项公式，根据已知化简即可
（2）求集合中元素个数
求集合中元素的个数
先当作纯粹数列题，求出，和，得出k与m的关系，再根据m的范围得出结论
设问
已知量
模型应用
（1）求两数列通项公式
，，
由已知求a2，求，得代入已知可得
（2）求和
数列中不在数列中的项按从小到大的顺序构成数列
由（1），推出“数列的前100项是由数列的前107项去掉数列的前7项后构成的”，
《专题2 数列 【讲】--大题精做（题型破局）》参考答案：
1．(1)，
(2)
【分析】（1）根据，作差得到，再根据等差数列通项公式计算可得；
（2）由（1）可得，利用并项求和法计算可得；
【详解】（1）解：当时，，解得，
由题知①，②，
由②①得，因为，所以，
于是：数列的奇数项是以为首项，以4为公差的等差数列，
即，
偶数项是以为首项，以4为公差的等差数列，
即
所以的通项公式；
（2）解：由（1）可得，
.
2．(1)
(2)见解析
【分析】（1）利用等差数列的通项公式求得，得到，利用和与项的关系得到当时，,进而得：，利用累乘法求得，检验对于也成立，得到的通项公式；
（2）由（1）的结论，利用裂项求和法得到，进而证得.
【详解】（1）∵，∴,∴,
又∵是公差为的等差数列，
∴,∴,
∴当时，，
∴,
整理得：,
即,
∴
，
显然对于也成立，
∴的通项公式；
（2）
∴
3．(1)
(2)5
【分析】（1）由题干中的条件，得数列是公差为1的等差数列，求出，再利用即可求出数列的通项公式.
（2）利用裂项相消求出，再解不等式即可.
【详解】（1））由，得数列是公差为1的等差数列，
又，，．
当时，，
又也满足上式，
（2）由（1）知，，
．
由得，得，
，
∴n的最小值为5．
4．(1)证明见解析，
(2)
【分析】（1）通过构造思想，等式两边同时加1，即可证得等比数列，再求通项公式即可；
（2）利用错位相减法直接求和即可.
【详解】（1）由，
所以是首项、公比均为3的等比数列，故
所以.
（2）由（1）有，则，
所以，
两式相减，得
所以.
5．(1)，；
(2).
【分析】（1）根据等差数列的通项公式和等比中项的性质可求出，再根据等差数列的通项公式和前项和公式即可求解；
（2）结合题意，由（1）的结论可得，利用裂项相消法即可求解.
【详解】（1）设等差数列的公差为，则，
由成等比数列，得， 则，即，
而，解得，所以，.
（2）由（1）知，又，则，
因此，
所以.