中考数学二轮培优题型训练压轴题14以四边形为背景的几何类比探究压轴问题（2份，原卷版+解析版）

这是一份中考数学二轮培优题型训练压轴题14以四边形为背景的几何类比探究压轴问题（2份，原卷版+解析版），文件包含中考数学二轮培优题型训练压轴题14以四边形为背景的几何类比探究压轴问题原卷版doc、中考数学二轮培优题型训练压轴题14以四边形为背景的几何类比探究压轴问题解析版doc等2份试卷配套教学资源，其中试卷共74页， 欢迎下载使用。
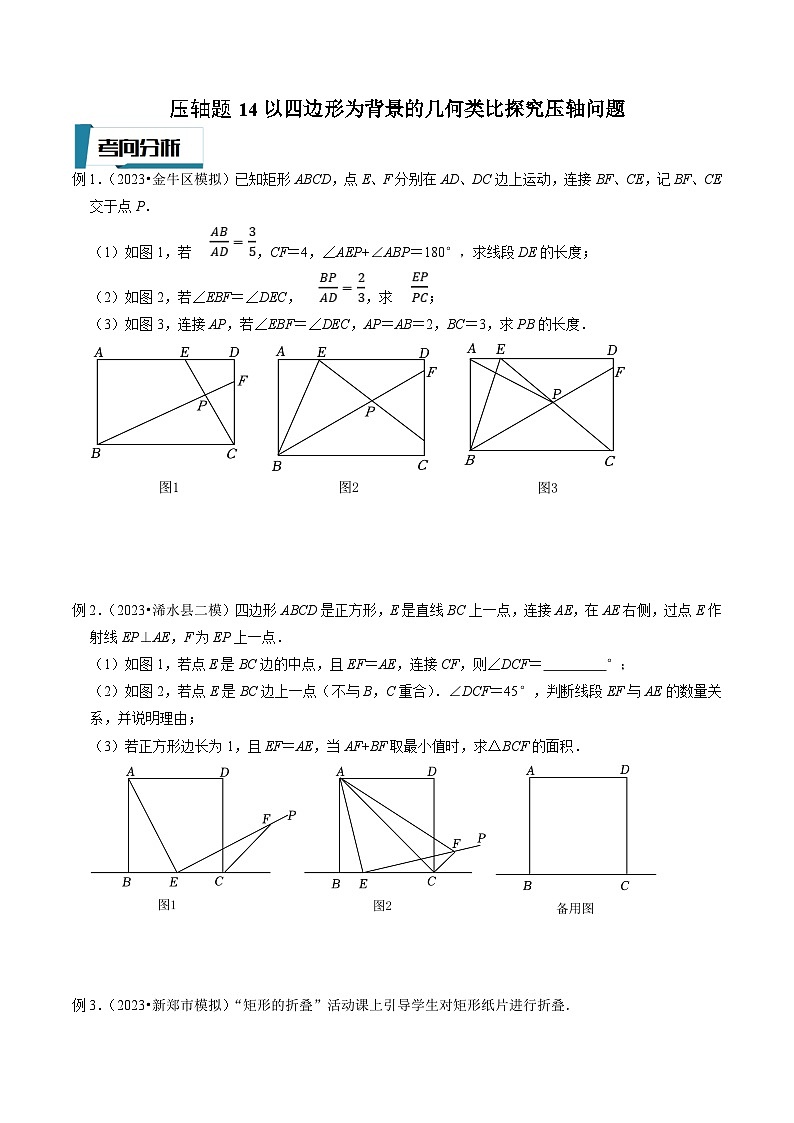
例1．（2023•金牛区模拟）已知矩形ABCD，点E、F分别在AD、DC边上运动，连接BF、CE，记BF、CE交于点P．
（1）如图1，若，CF＝4，∠AEP+∠ABP＝180°，求线段DE的长度；
（2）如图2，若∠EBF＝∠DEC，，求；
（3）如图3，连接AP，若∠EBF＝∠DEC，AP＝AB＝2，BC＝3，求PB的长度．
例2．（2023•浠水县二模）四边形ABCD是正方形，E是直线BC上一点，连接AE，在AE右侧，过点E作射线EP⊥AE，F为EP上一点．
（1）如图1，若点E是BC边的中点，且EF＝AE，连接CF，则∠DCF＝ °；
（2）如图2，若点E是BC边上一点（不与B，C重合）．∠DCF＝45°，判断线段EF与AE的数量关系，并说明理由；
（3）若正方形边长为1，且EF＝AE，当AF+BF取最小值时，求△BCF的面积．
例3．（2023•新郑市模拟）“矩形的折叠”活动课上引导学生对矩形纸片进行折叠．
如图，将矩形纸片ABCD折叠，点A与点D重合，点C与点B重合，将纸片展开，折痕为EF，在AD边上找一点P，沿CP将△PCD折叠，得到△PCQ，点D的对应点为点Q．
问题提出：
（1）若点Q落在EF上，CD＝2，连接BQ．
①△CQB是 三角形；
②若△CQB是等边三角形，则AD的长为 ．
深入探究：
（2）在（1）的条件下，当AD＝2时，判断△CQB的形状并证明；
拓展延伸；
（3）若AB＝6，AD＝8，其他条件不变，当点Q落在矩形ABFE内部（包括边）时，连接AQ，直接写出AQ的取值范围．
例4．（2023•莱西市一模）如图，在四边形ABCD中，AB∥CD，∠ABC＝90°，AB＝8cm，BC＝6cm，AD＝10cm，点P、Q分别是线段CD和AD上的动点．点P以2cm/s的速度从点D向点C运动，同时点Q以1cm/s的速度从点A向点D运动，当其中一点到达终点时，两点停止运动，将PQ沿AD翻折得到QP'，连接PP'交直线AD于点E，连接AC、BQ．设运动时间为t（s），回答下列问题：
（1）当t为何值时，PQ∥AC？
（2）求四边形BCPQ的面积S（cm2）关于时间t（s）的函数关系式；
（3）是否存在某时刻t，使点Q在∠PP'D平分线上？若存在，求出t的值；若不存在，请说明理由．
1．（2023•南关区校级模拟）实践与探究
操作一：如图①，将矩形ABCD对折，使点A与点D重合，点B与点C重合，折痕为EF．展平后，将矩形ABCD沿过点B的直线折叠，折痕为BG，点G在AD边上，使点A的对应点A′
落在EF上，连接A′C．若点G、A′、C共线，求证：△BA′C≌△GDC；
操作二：如图②，在矩形ABCD中，AB＝6，BC＝8，若矩形ABCD沿过点B的直线折叠，点G在AD边上，折痕为BG，点A的对应点A′落在矩形ABCD的内部．
（1）连接A′D，A′D的最小值为 ；
（2）如图③，将矩形ABCD再沿过点B的直线折叠，使点C在直线A′B边上．折痕为BH，点C的对应点为点C′，将矩形沿过点H的直线继续折叠，点R在AD上，折痕为HR，点D的对应点为点D′．我们发现，点R的位置不同，点D′的位置也不同，当点D′恰好与点C′重合时，线段RD的长为 ．
2．（2023•范县一模）综合与实践综合与实践课上，老师与同学们以“特殊的三角形”为主题开展数学活动．
（1）操作判断 如图1，在△ABC中，∠BAC＝90°，AB＝AC，点E在AC上（且不与点A、C重合）在△ABC的外部作△CED，使∠CED＝90°，ED＝EC，连接AD，过点B作BF∥AD，过点D作DF∥AB，BF交DF于点F，连接AF．
根据以上操作，判断：四边形ABFD的形状是 ；三角形△AEF的形状是 ；
​
（2）迁移探究明明同学所在的“认真•坚持”学习小组“异想天开”，将△CED绕点C逆时针旋转，如图2，当点E落在线段BC上时，请你：
①求证：四边形ABFD的是矩形；
②连接AE、AF，若AE＝3，求AF的长；
（3）拓展应用亮亮同学所在的“感恩•责任”学习小组受此启发，将△CED绕点C继续逆时针旋转，能使四边形ABFD为菱形，若AB＝6，CE＝2，请你直接写出线段AF的长．
3．（2023•息县模拟）某数学兴趣小组在数学实践课上开展了“菱形折叠”研究活动．
第一步：每人制作内角不同，边长都为2的菱形若干个，四个顶点为A，B，C，D（为保持一致，活动中，小组内制作图形各点名称命名规则相同）；
第二步：对折找到一条对角线BD并展开；
第三步：将边AB折叠到对角线BD所在直线上，顶点A的落点为F，所得折痕与边AD交于点E；
第四步：测量∠A，∠FDE，∠FED的度数．
（1）小组长在研究大家测得的数据后仔细分析，发现可以通过∠A的度数，计算得到∠FED和∠FDE的度数．如图，若一位同学制作的菱形中∠A＝30°，请你给出此时∠FDE和∠FED的度数：∠FDE＝ °，∠FED＝ °．
（2）若∠A＜60°，请探究∠A的度数为多少时，△DEF为等腰三角形，并说明理由；
（3）请直接写出△DEF为直角三角形时DF的长．​
4．（2023•南湖区校级二模）如图，在菱形ABCD中，AB＝25． ，点O是AD边的中点．连结BD．点P是折线AB﹣BD上一点，连结OP．点A关于OP的对称点为A′．
（1）对 角线BD的长为 ；
（2）当点A′落在△ABD的边上（点A′不与点A、D重合）时，求AP的长；
（3）连结A′C，求线段A′C的长的最小值；
（4）当OA′所在的直线垂直于AB时，直接写出线段BP的长．
5．（2023•天山区一模）某校数学活动小组探究了如下数学问题：
（1）问题发现：如图1，△ABC中，∠BAC＝90°，AB＝AC．点P是底边BC上一点，连接AP，以AP为腰作等腰Rt△APQ，且∠PAQ＝90°，连接CQ、则BP和CQ的数量关系是 ；
（2）变式探究：如图2，△ABC中，∠BAC＝90°，AB＝AC．点P是腰AB上一点，连接CP，以CP为底边作等腰Rt△CPQ，连接AQ，判断BP和AQ的数量关系，并说明理由；
（3）问题解决；如图3，正方形ABCD的边长为10，点P是边AB上一点，以DP为对角线作正方形DEPQ，连接AQ．若设正方形DEPQ的面积为y，AQ＝x．求y与x的函数关系式．
6．（2023•泰山区一模）问题：如图，在▱ABCD中，AB＝9，AD＝6，∠DAB，∠ABC的平分线AE，BF分别与直线CD交于点E，F．
（1）求EF的长．
探究：
（2）把“问题”中的条件“AB＝9”去掉，其余条件不变．当点E与点C重合时，求EF的长．
（3）把“问题”中的条件“AB＝9，AD＝6”去掉，其余条件不变，当点C，D，E，F相邻两点间的距离相等时，求的值．
7．（2023•靖江市模拟）如图，在矩形ABCD中，．点E、F分别在AD、BC上，四边形BEDF为菱形．
（1）利用尺规作图在图1中作出菱形BEDF（不写作法，保留作图痕迹）．
（2）如图2，动点M从点E出发沿射线ED方向运动，同时，动点N从点F出发沿射线DF方向运动，且M、N两点运动速度相同，BM、EN相交于点P．
①求∠EPM的度数．
②连接CP，线段CP长度的最小值为 ．
8．（2023•城阳区一模）已知：如图①，菱形ABCD中，对角线AC，BD相交于点O，且AC＝12cm，BD＝16cm．点P从点A出发，沿AB方向匀速运动，速度为1cm/s；同时，直线EF从点D出发，沿DB方向匀速运动，速度为1cm/s，EF⊥BD，且与AD，BD，CD分别交于点E，Q，F；当直线EF停止运动时，点P也停止运动．连接PC、PE，设运动时间为t（s）（0＜t＜8）．解答下列问题：
（1）当t为何值时，点A在线段PE的垂直平分线上？
（2）设四边形PCFE的面积为y（cm2），求y与t之间的函数关系式；
（3）如图②，连接PO、EO，是否存在某一时刻t，使∠POE＝90°？若存在，求出t的值；若不存在，请说明理由．
9．（2023•雁塔区校级模拟）问题情​境
如图，在四边形ABCD中，连接BD，∠ABD＝∠BCD＝90°，∠ADB＝30°，∠BDC＝45°，AB＝2，点E为AD的中点，连接CE．以点D为中心，顺时针旋转△DEC，得到△DGF，点E，C的对应点分别为点G，F．
问题探究
（1）如图①，则CE的长为 ；
（2）如图②，在△DFG旋转过程中，当B，F，G三点共线时，求△ABF的面积；
（3）如图③，在△DFG旋转过程中，连接AF，AG，直接写出△AFG面积的最大值．
10．（2023•张店区一模）如图1，边长为2的正方形ABCD中，点P为边BC上一个动点，连接AP，作MN⊥AP于点E，交边AB于M，交边CD于N．
（1）求证：MN＝AP；
（2）如图2，连接BD，线段MN交BD于点F，点E为AP的中点．
①当BP＝1时，求EF的长；
②线段EF是否存在最小值和最大值，若存在，请直接写出线段EF的最小值和最大值，若不存在，请说明理由．
11．（2023•包河区校级一模）如图，AM是△ABC的中线，D是线段AM上一点（不与点A重合）．DE∥AB交AC于点F，CE∥AM，连接AE．如图1，当点D与M重合时，四边形ABDE是平行四边形．
（1）如图2，当点D不与M重合时，判断四边形ABDE的形状，并说明理由．
（2）如图3，延长BD交AC于点H，若BH⊥AC，且BH＝AM．
①求∠CAM的度数；
②当，DM＝4时，求DH的长．
12．（2023•内黄县二模）综合与实践综合与实践课上，老师与同学们以“特殊的三角形”为主题开展数学活动．
（1）操作判断如图1，
在△ABC中，∠ABC＝90°，AB＝BC，点P是直线AC上一动点．
操作一：连接BP，将线段BP绕点P逆时针旋转 90° 得到PD，连接DC，如图2．
根据以上操作，判断：如图3，当点P与点A重合时，则四边形ABCD的形状是 ；
（2）迁移探究
①如图4，当点P与点C重合时，连接DB，判断四边形ABDC的形状，并说明理由；
②当点P与点A，点C都不重合时，试猜想DC与BC的位置关系，并利用图2证明你的猜想；
（3）拓展应用当点P与点A，点C都不重合时，若AB＝3，AP＝2，请直接写出CD的长．
13．（2023•东莞市校级模拟）如图（1），在Rt△ABC中，．点D是BC边上任意一点（不与B，C重合），连接AD，过点D作DE⊥AB于点E，连接CE，点F为AD中点，连接CF，EF．
（1）当BD＝2CD时，判断四边形CDEF的形状，并证明．
（2）点D在线段BC上的什么位置时，△DEF的面积最大？请说明理由．
（3）如图（1）中的△BDE绕点B旋转到如图（2）所示位置，得到△BD′E′，使得点A在直线D′E′上，连接CE′，点F′为AD′中点，AD′与BC交于点G，其他条件不变．求证：AE′﹣D′E′＝2CF′．
14．（2023•利辛县模拟）综合与实践
问题解决：
（1）已知四边形ABCD是正方形，以B为顶点作等腰直角三角形BEF，BE＝BF，连接AE．如图1，当点E在BC上时，请判断AE和CF的关系，并说明理由．
问题探究：
（2）如图2，点H是AE延长线与直线CF的交点，连接BH，将△BEF绕点B旋转，当点F在直线BC右侧时，求证：；
问题拓展：
（3）将△BEF绕点B旋转一周，当∠CFB＝45°时，若AB＝3，BE＝1，请直接写出线段CH的长．
15．（2023•临安区一模）如图，正方形ABCD，对角线AC与BD交于点O，E是线段OC上一点，以BE为边在BD的右下方作等边三角形BEF，连结DE，DF．
（1）求证：△ABE≌△ADE．
（2）∠BDF的度数改变吗？若不变，请求出这个角的值．
（3）若，求FD的最小值．
16．（2023•南明区校级模拟）利用“平行+垂直”作延长线或借助“平行+角平分线”构造等腰三角形是我们解决几何问题的常用方法．
（1）发现：如图1，AB∥CD，CB平分∠ACD，求证：△ABC是等腰三角形．
（2）探究：如图2，AD∥BC，BD平分∠ABC，BD⊥CD于D，若BC＝6，求AB．
（3）应用：如图3，在▱ABCD中，点E在AD上，且BE平分∠ABC，过点E作EF⊥BE交BC的延长线于点F，交 CD于点M，若AD＝7，CF＝3，tan∠EBF＝3，求BD的长．
​
17．（2023•虎林市校级一模）已知四边形ABCD是菱形，点E，F分别在边AD，CD上，DE＝DF，．
（1）如图1，当∠ABC＝120°时，易证：（不需证明）；
（2）当∠ABC＝60°时，如图2；当∠ABC＝30°，如图3，线段AE，CF，EF之间有怎样的数量关系？请直接写出你的猜想，并对图3加以证明．
18．（2023•市南区一模）如图，在Rt△ABC中，∠C＝90°，AB＝10cm，AC＝6cm．点E从A出发，沿AB方向向B匀速运动，速度是1cm/s；同时，点F从B出发，沿BC方向向C匀速运动，速度是2cm/s．将△AEF沿AF折叠，E的对称点为G．设运动时间为t（s）（0＜t＜4），请回答下列问题：
（1）t为何值时，BE＝BF；
（2）设四边形ABFG的面积为S（cm2），求S关于t的函数关系式；
（3）是否存在某一时刻t，使得点G落在线段AC上？若存在，求出t的值；若不存在，请说明理由；
（4）是否存在某一时刻t，使得四边形AEFG为菱形？若存在，求出t的值；若不存在，请说明理由．
19．（2023•崂山区一模）已知：如图1，在四边形ABCD中，∠ADC＝∠C＝90°，AD＝DC＝8cm，BC＝6cm，连接BD，点P从点A出发，沿AD方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s，连接PQ，设运动时间为t（s）（0＜t＜5）．
（1）当t为何值时，点D在线段PQ的垂直平分线上？
（2）延长PQ交BC于点E（如图2），若四边形APEB是平行四边形．求t的值；
（3）设△DPQ的面积为ycm2，求y与t的函数关系式，并求y的最大值；
（4）是否存在某一时刻t，使得PQ与BD的夹角为45°？若存在，请求出此时t的值；若不存在，请说明理由．
20．（2023•市南区一模）在数学兴趣社团课上，同学们对平行四边形进行了深入探究．
探究一：如图1，在矩形ABCD中，AC2＝AB2+BC2，BD2＝AC2＝CD2+AD2，则AC2+BD2＝AB2+BC2+CD2+AD2，由此得出结论：矩形两条对角线的平方和等于其四边的平方和．
探究二：对于一般的平行四边形，是否仍有上面的结论呢？
证明：如图2，在▱ABCD中，过A作AM⊥BC于M，过D作DN⊥BC，交BC延长线于N．设AB＝a，BC＝b，BM＝x，AM＝y，
∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∴∠ABC＝∠DCN，
又∵∠AMB＝∠DNC＝90°，∴△ABM≌△DCN．
∴CN＝BM＝x，DN＝AM＝y．
请你接着完成上面的证明过程．
结论应用：若一平行四边形的周长为20，两条对角线长分别为8，2，求该平行四边形的四条边长．