中考数学二轮培优复习专题09 几何中最小值计算压轴真题训练（2份，原卷版+解析版）

这是一份中考数学二轮培优复习专题09 几何中最小值计算压轴真题训练（2份，原卷版+解析版），文件包含中考数学二轮培优复习专题09几何中最小值计算压轴真题训练原卷版doc、中考数学二轮培优复习专题09几何中最小值计算压轴真题训练解析版doc等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。

【答案】6
【解答】解：如图，作点B关于AC的对称点B'，交AC于点F，连接B′E交AC于点P，则PE+PB的最小值为B′E的长度，
∵四边形ABCD为矩形，
∴AB＝CD＝4，∠ABC＝90°，
在Rt△ABC中，AB＝4，BC＝4，
∴tan∠ACB＝＝，
∴∠ACB＝30°，
由对称的性质可知，B'B＝2BF，B'B⊥AC，
∴BF＝BC＝2，∠CBF＝60°，
∴B′B＝2BF＝4，
∵BE＝BF，∠CBF＝60°，
∴△BEF是等边三角形，
∴BE＝BF＝B'F，
∴△BEB'是直角三角形，
∴B′E＝＝＝6，
∴PE+PB的最小值为6，
故答案为：6．
2．（2022•自贡）如图，矩形ABCD中，AB＝4，BC＝2，G是AD的中点，线段EF在边AB上左右滑动，若EF＝1，则GE+CF的最小值为 ．
【答案】3
【解答】解：解法一：如图，作G关于AB的对称点G'，在CD上截取CH＝1，然后连接HG'交AB于E，在EB上截取EF＝1，此时GE+CF的值最小，
∵CH＝EF＝1，CH∥EF，
∴四边形EFCH是平行四边形，
∴EH＝CF，
∴G'H＝EG'+EH＝EG+CF，
∵AB＝4，BC＝AD＝2，G为边AD的中点，
∴DG'＝AD+AG'＝2+1＝3，DH＝4﹣1＝3，
由勾股定理得：HG'＝＝3，
即GE+CF的最小值为3．
解法二：∵AG＝AD＝1，
设AE＝x，则BF＝AB﹣EF﹣AE＝4﹣x﹣1＝3﹣x，
由勾股定理得：EG+CF＝+，
如图，矩形EFGH中，EH＝3，GH＝2，GQ＝1，
P为FG上一动点，设PG＝x，则FP＝3﹣x，
∴EP+PQ＝+，
当E，P，Q三点共线时，EP+PQ最小，最小值是3，
即EG+CF的最小值是3．
故答案为：3．
3．（2022•鄂州）如图，定直线MN∥PQ，点B、C分别为MN、PQ上的动点，且BC＝12，BC在两直线间运动过程中始终有∠BCQ＝60°．点A是MN上方一定点，点D是PQ下方一定点，且AE∥BC∥DF，AE＝4，DF＝8，AD＝24，当线段BC在平移过程中，AB+CD的最小值为（ ）
A．24B．24C．12D．12
【答案】C
【解答】解：如图，
作DL⊥PQ于L，过点A作PQ的垂线，过点D作PQ的平行线，它们交于点R，延长DF至T，使DT＝BC＝12，连接AT，
AT交MN于B′，作B′C′∥BC，交PQ于C′，则当BC在B′C′时，AB+CD最小，最小值为AT的长，
可得AK＝AE•sin60°＝＝2，DL＝＝4，＝6，
∴AR＝2+6+4＝12，
∵AD＝24，
∴sin∠ADR＝＝，
∴∠ADR＝30°，
∵∠PFD9＝60°，
∴∠ADT＝90°，
∴AT＝＝＝12，
故答案为：C．
4．（2022•贺州）如图，在矩形ABCD中，AB＝8，BC＝6，E，F分别是AD，AB的中点，∠ADC的平分线交AB于点G，点P是线段DG上的一个动点，则△PEF的周长最小值为 ．
【答案】5+
【解答】解：如图，在DC上截取DT，使得DT＝DE，连接FT，过点T作TH⊥AB于点H．
∵四边形ABCD是矩形，
∴∠A＝∠ADT＝90°，
∵∠AHT＝90°，
∴四边形AHTD是矩形，
∵AE＝DE＝AD＝3．AF＝FB＝AB＝4，
∴AH＝DT＝3，HF＝AF﹣AH＝4﹣3＝1，HT＝AD＝6，
∴FT＝＝＝，
∵DG平分∠ADC，DE＝DT，
∴E、T关于DG对称，
∴PE＝PT，
∴PE+PF＝PF+PT≥FT＝，
∵EF＝＝＝5，
∴△EFP的周长的最小值为5+，
故答案为：5+．
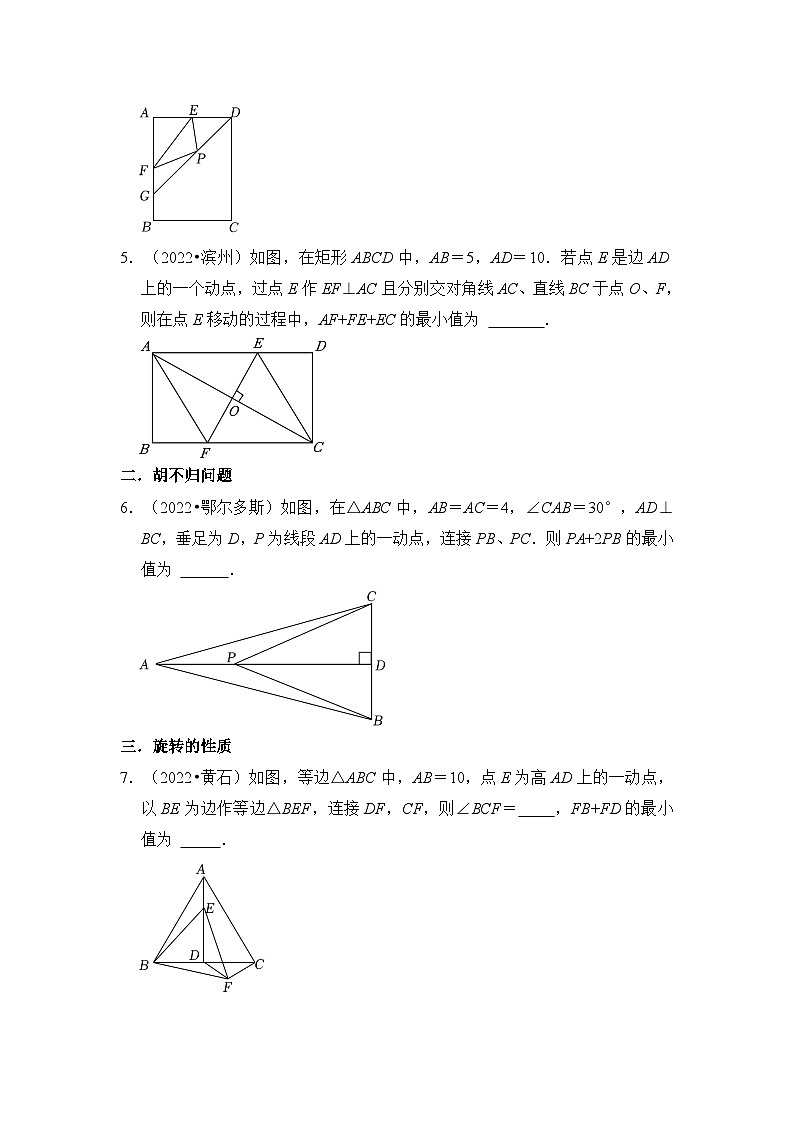
5．（2022•滨州）如图，在矩形ABCD中，AB＝5，AD＝10．若点E是边AD上的一个动点，过点E作EF⊥AC且分别交对角线AC、直线BC于点O、F，则在点E移动的过程中，AF+FE+EC的最小值为 ．
【答案】+
【解答】解：如图，过点E作EH⊥BC于点H．
∵四边形ABCD是矩形，
∴∠B＝∠BAD＝∠BHE＝90°，
∴四边形ABHE是矩形，
∴EH＝AB＝5，
∵BC＝AD＝10，
∴AC＝＝＝5，
∵EF⊥AC，
∴∠COF＝90°，
∴∠EFH+∠ACB＝90°，
∵∠BAC+∠ACB＝90°，
∴∠EFH＝∠BAC，
∴△EHF∽△CBA，
∴＝＝，
∴＝＝，
∴FH＝，EF＝，
设BF＝x，则DE＝10﹣x﹣＝﹣x，
∵EF是定值，
∴AF+CE的值最小时，AF+EF+CE的值最小，
∵AF+CE＝+，
∴欲求AF+CE的最小值相当于在x轴上找一点P（x，0），使得P到A（0，5），B（，5）的距离和最小，如图1中，
作点A关于x轴的对称点A′，连接BA′交xz轴于点P，连接AP，此时PA+PB的值最小，最小值为线段A′B的长，
∵A′（0，﹣5），B（，5），
∴A′B＝＝，
∴AF+CE的最小值为，
∴AF+EF+CE的最小值为+．
解法二：过点C作CC′∥EF，使得CC′＝EF，连接C′F．
∵EF＝CC′，EF∥CC′，
∴四边形EFC′C是平行四边形，
∴EC＝FC′，
∵EF⊥AC，
∴AC⊥CC′，
∴∠ACC＝90°，
∵AC′＝＝＝，
∴AF+EC＝AF+FC′≥AC′＝，
∴AF+EF+CE的最小值为+．
故答案为：+
二．胡不归问题
6．（2022•鄂尔多斯）如图，在△ABC中，AB＝AC＝4，∠CAB＝30°，AD⊥BC，垂足为D，P为线段AD上的一动点，连接PB、PC．则PA+2PB的最小值为 ．
【答案】4
【解答】解：如图，
在∠BAC的外部作∠CAE＝15°，作BF⊥AE于F，交AD于P，
此时PA+2PB最小，
∴∠AFB＝90°
∵AB＝AC，AD⊥BC，
∴∠CAD＝∠BAD＝，
∴∠EAD＝∠CAE+∠CAD＝30°，
∴PF＝，
∴PA+2PB＝2（）＝2（PF+PB）＝2BF，
在Rt△ABF中，AB＝4，∠BAF＝∠BAC+∠CAE＝45°，
∴BF＝AB•sin45°＝4×＝2，
∴（PA+2PB）最小＝2BF＝4，
故答案为：4．
三．旋转的性质
7．（2022•黄石）如图，等边△ABC中，AB＝10，点E为高AD上的一动点，以BE为边作等边△BEF，连接DF，CF，则∠BCF＝ ，FB+FD的最小值为 ．
【答案】30°5
【解答】解：如图，
∵△ABC是等边三角形，AD⊥CB，
∴∠BAE＝∠BAC＝30°，
∵△BEF是等边三角形，
∴∠EBF＝∠ABC＝60°，BE＝BF，
∴∠ABE＝∠CBF，
在△BAE和△BCF中，
，
∴△BAE≌△BCF（SAS），
∴∠BAE＝∠BCF＝30°，
作点D关于CF的对称点G，连接CG，DG，BG，BG交CF的延长线于点F′，连接DF′，此时BF′+DF′的值最小，最小值＝线段BG的长．
∵∠DCF＝∠FCG＝30°，
∴∠DCG＝60°，
∵CD＝CG＝5，
∴△CDG是等边三角形，
∴DB＝DC＝DG，
∴∠CGB＝90°，
∴BG＝＝＝5，
∴BF+DF的最小值为5，
故答案为：30°，5．
8．（2022•柳州）如图，在正方形ABCD中，AB＝4，G是BC的中点，点E是正方形内一个动点，且EG＝2，连接DE，将线段DE绕点D逆时针旋转90°得到线段DF，连接CF，则线段CF长的最小值为 ．
【答案】2﹣2
【解答】解：连接DG，将DG绕点D逆时针旋转90°得DM，连接MG，CM，MF，
作MH⊥CD于H，
∵∠EDF＝∠GDM，
∴∠EDG＝∠FDM，
∵DE＝DF，DG＝DM，
∴△EDG≌△MDF（SAS），
∴MF＝EG＝2，
∵∠GDC＝∠DMH，∠DCG＝∠DHM，DG＝DM，
∴△DGC≌△MDH（AAS），
∴CG＝DH＝2，MH＝CD＝4，
∴CM＝＝2，
∵CF≥CM﹣MF，
∴CF的最小值为2﹣2，
故答案为：2﹣2．
9．（2022•广州）如图，在矩形ABCD中，BC＝2AB，点P为边AD上的一个动点，线段BP绕点B顺时针旋转60°得到线段BP′，连接PP′，CP′．当点P′落在边BC上时，∠PP′C的度数为 ；当线段CP′的长度最小时，∠PP′C的度数为 ．
【答案】120°，75°
【解答】解：如图，以AB为边向右作等边△ABE，连接EP′．
∵△BPP′是等边三角形，
∴∠ABE＝∠PBP′＝60°，BP＝BP′，BA＝BE，
∴∠ABP＝∠EBP′，
在△ABP和△EBP′中，
，
∴△ABP≌△EBP′（SAS），
∴∠BAP＝∠BEP′＝90°，
∴点P′在射线EP′上运动，
如图1中，设EP′交BC于点O，
当点P′落在BC上时，点P′与O重合，此时∠PP′C＝180°﹣60°＝120°，
当CP′⊥EP′时，CP′的长最小，此时∠EBO＝∠OCP′＝30°，
∴EO＝OB，OP′＝OC，
∴EP′＝EO+OP′＝OB+OC＝BC，
∵BC＝2AB，
∴EP′＝AB＝EB，
∴∠EBP′＝∠EP′B＝45°，
∴∠BP′C＝45°+90°＝135°，
∴∠PP′C＝∠BP′C﹣∠BP′P＝135°﹣60°＝75°．
故答案为：120°，75°．
10．（2022•无锡）△ABC是边长为5的等边三角形，△DCE是边长为3的等边三角形，直线BD与直线AE交于点F．如图，若点D在△ABC内，∠DBC＝20°，则∠BAF＝ °；现将△DCE绕点C旋转1周，在这个旋转过程中，线段AF长度的最小值是 ．
【答案】80，4﹣．
【解答】解：∵△ACB，△DEC都是等边三角形，
∴AC＝CB，DC＝EC，∠ACB＝∠DCE＝60°，
∴∠BCD＝∠ACE，
在△BCD和△ACE中，
，
∴△BCD≌△ACE（SAS），
∴∠DBC＝∠EAC＝20°，
∵∠BAC＝60°，
∴∠BAF＝∠BAC+∠CAE＝80°．
如图1中，设BF交AC于点T．
同法可证△BCD≌△ACE，
∴∠CBD＝∠CAF，
∵∠BTC＝∠ATF，
∴∠BCT＝∠AFT＝60°，
∴点F在△ABC的外接圆上运动，当∠ABF最小时，AF的值最小，此时CD⊥BD，
∴BD＝＝＝4，
∴AE＝BD＝4，∠BDC＝∠AEC＝90°，
∵CD＝CE，CF＝CF，
∴Rt△CFD≌Rt△CFE（HL），
∴∠DCF＝∠ECF＝30°，
∴EF＝CE•tan30°＝，
∴AF的最小值＝AE﹣EF＝4﹣，
故答案为：80，4﹣．
四．折叠有关最值问题
11．（2022•青岛）如图，已知△ABC，AB＝AC，BC＝16，AD⊥BC，∠ABC的平分线交AD于点E，且DE＝4．将∠C沿GM折叠使点C与点E恰好重合．下列结论正确的有： ．（填写序号）
①BD＝8
②点E到AC的距离为3
③EM＝
④EM∥AC
【答案】①④
【解答】解：在△ABC中，AB＝AC，BC＝16，AD⊥BC，
∴BD＝DC＝BC＝8，故①正确；
如图，过点E作EF⊥AB于点F，EH⊥AC于点H，
∵AD⊥BC，AB＝AC，
∴AE平分∠BAC，
∴EH＝EF，
∵BE是∠ABD的角平分线，
∵ED⊥BC，EF⊥AB，
∴EF＝ED，
∴EH＝ED＝4，故②错误；
由折叠性质可得：EM＝MC，DM+MC＝DM+EM＝CD＝8，
设DM＝x，则EM＝8﹣x，
Rt△EDM中，EM2＝DM2+DE2，
∴（8﹣x）2＝42+x2，
解得：x＝3，
∴EM＝MC＝5，故③错误；
设AE＝a，则AD＝AE+ED＝4+a，BD＝8，
∴AB2＝（4+a）2+82，
∵＝，
∴，
∴，
∴AB＝2a，
∴（4+a）2+82＝（2a）2，
解得：a＝或a＝﹣4（舍去），
∴tanC＝＝，
又∵tan∠EMD＝，
∴∠C＝∠EMD，
∴EM∥AC，故④正确，
故答案为：①④．
12．（2022•铜仁市）如图，在边长为2的正方形ABCD中，点E为AD的中点，将△CDE沿CE翻折得△CME，点M落在四边形ABCE内．点N为线段CE上的动点，过点N作NP∥EM交MC于点P，则MN+NP的最小值为 ．
【答案】
【解答】解：作点P关于CE的对称点P′，
由折叠的性质知CE是∠DCM的平分线，
∴点P′在CD上，
过点M作MF⊥CD于F，交CE于点G，
∵MN+NP＝MN+NP′≥MF，
∴MN+NP的最小值为MF的长，
连接DG，DM，
由折叠的性质知CE为线段DM的垂直平分线，
∵AD＝CD＝2，DE＝1，
∴CE＝＝，
∵CE×DO＝CD×DE，
∴DO＝，
∴EO＝，
∵MF⊥CD，∠EDC＝90°，
∴DE∥MF，
∴∠EDO＝∠GMO，
∵CE为线段DM的垂直平分线，
∴DO＝OM，∠DOE＝∠MOG＝90°，
∴△DOE≌△MOG，
∴DE＝GM，
∴四边形DEMG为平行四边形，
∵∠MOG＝90°，
∴四边形DEMG为菱形，
∴EG＝2OE＝，GM＝DE＝1，
∴CG＝，
∵DE∥MF，即DE∥GF，
∴△CFG∽△CDE，
∴，即，
∴FG＝，
∴MF＝1+＝，
∴MN+NP的最小值为；
方法二：同理方法一得出MN+NP的最小值为MF的长，DO＝，
∴OC＝＝，DM＝2DO＝，
∵S△CDM＝DM•OC＝CD•MF，
即×＝2×MF，
∴MF＝，
∴MN+NP的最小值为；
故答案为：．
13．（2022•辽宁）如图，正方形ABCD的边长为10，点G是边CD的中点，点E是边AD上一动点，连接BE，将△ABE沿BE翻折得到△FBE，连接GF，当GF最小时，AE的长是 ．
【答案】5﹣5
【解答】解：∵将△ABE沿BE翻折得到△FBE，
∴BF＝BA＝10，
∴点F在以B为圆心，10为半径的圆上运动，
∴当点G、F、B三点共线时，GF最小，
连接EG，设AE＝x，
由勾股定理得，BG＝5，
∵S梯形ABGD＝S△EDG+S△ABE+S△EBG，
∴（5+10）×10＝++，
解得x＝5﹣5，
∴AE＝5﹣5，
故答案为：5﹣5．
14．（2022•台州）如图，在菱形ABCD中，∠A＝60°，AB＝6．折叠该菱形，使点A落在边BC上的点M处，折痕分别与边AB，AD交于点E，F．当点M与点B重合时，EF的长为 ；当点M的位置变化时，DF长的最大值为 ．
【答案】3，6﹣3．
【解答】解：如图1中，
∵四边形ABCD是菱形，
∴AD＝AB＝BC＝CD，∠A＝∠C＝60°，
∴△ADB，△BDC都是等边三角形，
当点M与B重合时，EF是等边△ADB的高，EF＝AD•sin60°＝6×＝3．
如图2中，连接AM交EF于点O，过点O作OK⊥AD于点K，交BC于点T，过点A作AG⊥CB交CB的延长线于点G，取AF的中点R，连接OR．
∵AD∥CG，OK⊥AD，
∴OK⊥CG，
∴∠G＝∠AKT＝∠GTK＝90°，
∴四边形AGTK是矩形，
∴AG＝TK＝AB•sin60°＝3，
∵OA＝OM，∠AOK＝∠MOT，∠AKO＝∠MTO＝90°，
∴△AOK≌△MOT（AAS），
∴OK＝OT＝，
∵OK⊥AD，
∴OR≥OK＝，
∵∠AOF＝90°，AR＝RF，
∴AF＝2OR≥3，
∴AF的最小值为3，
∴DF的最大值为6﹣3．
解法二：如图，过点D作DT⊥CB于点T．
∵DF＝AD﹣AF，
∴当AF最小时，DF的值最大，
∵AF＝FM≥DT＝3，
∴AF的最小值为3，
∴DF的最大值为6﹣3．
故答案为：3，6﹣3．
五．与圆有关最值计算
15．（2022•泸州）如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝2，半径为1的⊙O在Rt△ABC内平移（⊙O可以与该三角形的边相切），则点A到⊙O上的点的距离的最大值为 ．
【答案】2+1
【解答】解：当⊙O与BC、BA都相切时，连接AO并延长交⊙O于点D，则AD为点A到⊙O上的点的距离的最大值，
设⊙O与BC、BA的切点分别为E、F，连接OE、OF，
则OE⊥BC，OF⊥AB，
∵AC＝6，BC＝2，
∴tan∠ABC＝＝，AB＝＝4，
∴∠ABC＝60°，
∴∠OBF＝30°，
∴BF＝＝，
∴AF＝AB﹣BF＝3，
∴OA＝＝2，
∴AD＝2+1，
故答案为：2+1．
37．（2022•桂林）如图，某雕塑MN位于河段OA上，游客P在步道上由点O出发沿OB方向行走．已知∠AOB＝30°，MN＝2OM＝40m，当观景视角∠MPN最大时，游客P行走的距离OP是 米．
【答案】20
【解答】解：如图，取MN的中点F，过点F作FE⊥OB于E，以直径MN作⊙F，
∵MN＝2OM＝40m，点F是MN的中点，
∴MF＝FN＝20m，OF＝40m，
∵∠AOB＝30°，EF⊥OB，
∴EF＝20m，OE＝EF＝20m，
∴EF＝MF，
又∵EF⊥OB，
∴OB是⊙F的切线，切点为E，
∴当点P与点E重合时，观景视角∠MPN最大，
此时OP＝20m，
故答案为：20．