2024年山东省淄博市中考数学模拟试卷（原卷版）

这是一份2024年山东省淄博市中考数学模拟试卷（原卷版），共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
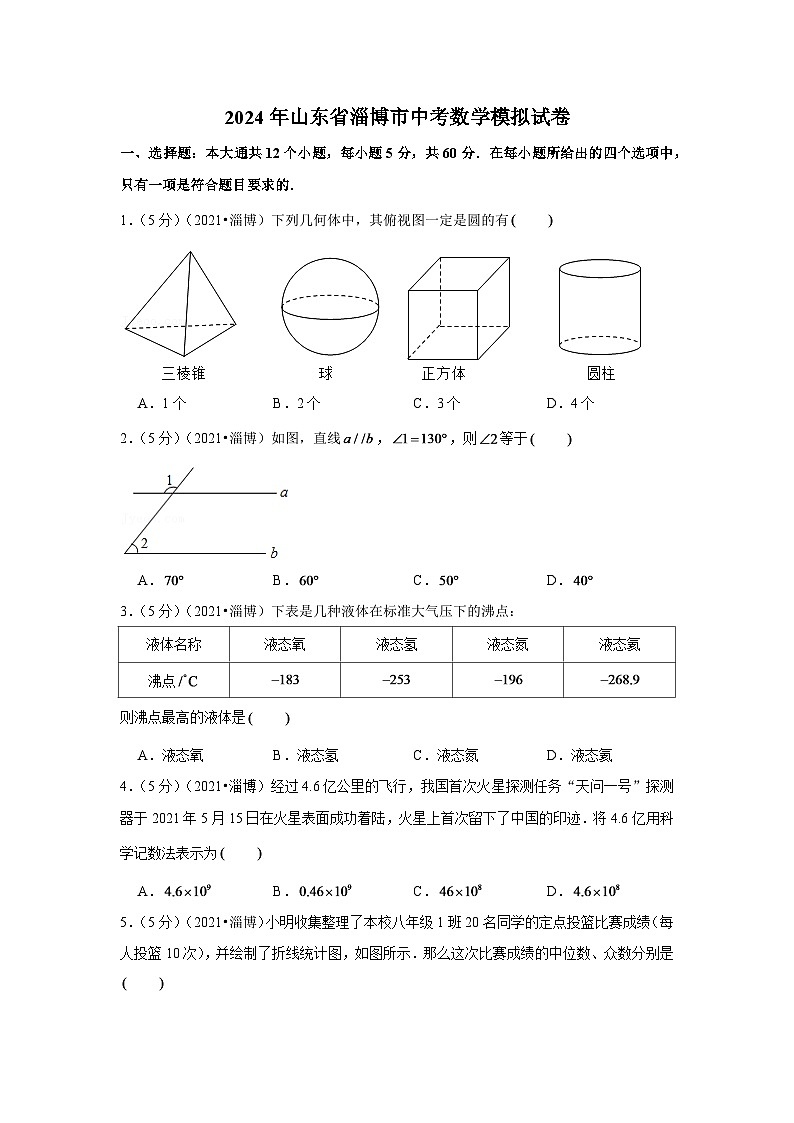
1．（5分）（2021•淄博）下列几何体中，其俯视图一定是圆的有
A．1个B．2个C．3个D．4个
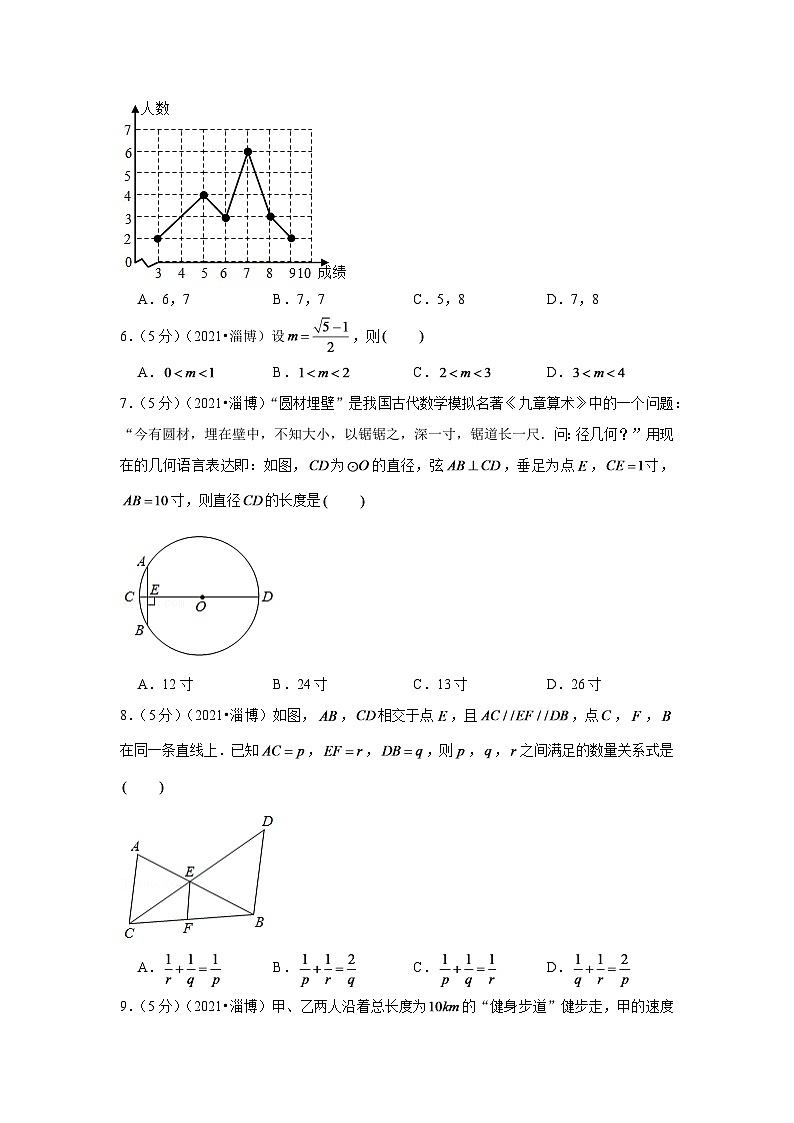
2．（5分）（2021•淄博）如图，直线，，则等于
A．B．C．D．
3．（5分）（2021•淄博）下表是几种液体在标准大气压下的沸点：
则沸点最高的液体是
A．液态氧B．液态氢C．液态氮D．液态氦
4．（5分）（2021•淄博）经过4.6亿公里的飞行，我国首次火星探测任务“天问一号”探测器于2021年5月15日在火星表面成功着陆，火星上首次留下了中国的印迹．将4.6亿用科学记数法表示为
A．B．C．D．
5．（5分）（2021•淄博）小明收集整理了本校八年级1班20名同学的定点投篮比赛成绩（每人投篮10次），并绘制了折线统计图，如图所示．那么这次比赛成绩的中位数、众数分别是
A．6，7B．7，7C．5，8D．7，8
6．（5分）（2021•淄博）设，则
A．B．C．D．
7．（5分）（2021•淄博）“圆材埋壁”是我国古代数学模拟名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，为的直径，弦，垂足为点，寸，寸，则直径的长度是
A．12寸B．24寸C．13寸D．26寸
8．（5分）（2021•淄博）如图，，相交于点，且，点，，在同一条直线上．已知，，，则，，之间满足的数量关系式是
A．B．C．D．
9．（5分）（2021•淄博）甲、乙两人沿着总长度为的“健身步道”健步走，甲的速度是乙的1.2倍，甲比乙提前12分钟走完全程．设乙的速度为，则下列方程中正确的是
A．B．
C．D．
10．（5分）（2021•淄博）已知二次函数的图象交轴于，两点．若其图象上有且只有，，三点满足，则的值是
A．1B．C．2D．4
11．（5分）（2021•淄博）如图，在中，，是斜边上的中线，过点作交于点．若，的面积为5，则的值为
A．B．C．D．
12．（5分）（2021•淄博）如图，在平面直角坐标系中，四边形的边与轴的正半轴重合，，轴，对角线，交于点．已知，的面积为4．若反比例函数的图象恰好经过点，则的值为
A．B．C．D．12
二、填空题：本大题共5个小题，每小题4分，共20分．
13．（4分）（2021•淄博）若分式有意义，则的取值范围是 ．
14．（4分）（2021•淄博）分解因式： ．
15．（4分）（2021•淄博）在直角坐标系中，点关于轴的对称点为，将点向左平移3个单位得到点，则的坐标为 ．
16．（4分）（2021•淄博）对于任意实数，抛物线与轴都有公共点，则的取值范围是 ．
17．（4分）（2021•淄博）两张宽为的纸条交叉重叠成四边形，如图所示．若，则对角线上的动点到，，三点距离之和的最小值是 ．
三、解答题：本大题共7个小题，共70分．解答要写出必要的文字说明，证明过程放演算步骤．
18．（8分）（2021•淄博）先化简，再求值：，其中，．
19．（8分）（2021•淄博）如图，在中，的平分线交于点，过点作交于点．
（1）求证：；
（2）若，，求的度数．
20．（10分）（2021•淄博）如图，在平面直角坐标系中，直线与双曲线相交于，两点．
（1）求，对应的函数表达式；
（2）过点作轴交轴于点，求的面积；
（3）根据函数图象，直接写出关于的不等式的解集．
21．（10分）（2021•淄博）为迎接中国共产党的百年华诞，某中学就有关中国共产党历史的了解程度，采取随机抽样的方式抽取本校部分学生进行了测试（满分100分），并将测试成绩进行了收集整理，绘制了如下不完整的统计图、表．
请根据统计图、表中所提供的信息，解答下列问题：
（1）统计表中的 ， ；成绩扇形统计图中“良好”所在扇形的圆心角是 度；
（2）补全上面的成绩条形统计图；
（3）若该校共有学生1600人，估计该校学生对中国共产党历史的了解程度达到良好以上（含良好）的人数．
22．（10分）（2021•淄博）为更好地发展低碳经济，建设美丽中国．某公司对其生产设备进行了升级改造，不仅提高了产能，而且大幅降低了碳排放量．已知该公司去年第三季度产值是2300万元，今年第一季度产值是3200万元，假设公司每个季度产值的平均增长率相同．
（1）求该公司每个季度产值的平均增长率；
（2）问该公司今年总产值能否超过1.6亿元？并说明理由．
23．（12分）（2021•淄博）已知：在正方形的边上任取一点，连接，一条与垂直的直线（垂足为点沿方向，从点开始向下平移，交边于点．
（1）当直线经过正方形的顶点时，如图1所示．求证：；
（2）当直线经过的中点时，与对角线交于点，连接，如图2所示．求的度数；
（3）直线继续向下平移，当点恰好落在对角线上时，交边于点，如图3所示．设，，，求与之间的关系式．
24．（12分）（2021•淄博）如图，在平面直角坐标系中，抛物线与轴交于，两点，与轴交于点，连接．
（1）若，求抛物线对应的函数表达式；
（2）在（1）的条件下，点位于直线上方的抛物线上，当面积最大时，求点的坐标；
（3）设直线与抛物线交于，两点，问是否存在点（在抛物线上），点（在抛物线的对称轴上），使得以，，，为顶点的四边形成为矩形？若存在，求出点，的坐标；若不存在，说明理由．
液体名称
液态氧
液态氢
液态氮
液态氦
沸点
成绩等级
分数段
频数（人数）
优秀
良好
较好
12
一般
10
较差
3
科学计算器按键顺序
计算结果（已取近似值）
解答过程中可直接使用表格中的数据哟！
1.18
1.39
1.64