2024年山东省淄博市中考数学模拟试卷（解析版）

这是一份2024年山东省淄博市中考数学模拟试卷（解析版），共23页。
本试卷共8页，满分150分，考试时间120分钟．考试结束后，将本试卷和答题卡一并交 回．
注意事项：
1．答题前，考生务必用0.5毫米黑色签字笔将区县、学校、姓名、考试号、座号填写在答题卡和试卷规定位置，并核对条形码．
2．选择题每小题选出答案后，用2B铅笔涂黑答题卡对应题目的答案标号；如需改动，用橡皮擦干净后，再选涂其他答案标号．
3．非选择题必须用0.5毫米黑色签字笔作答，字体工整、笔迹清晰，写在答题卡各题目指定区域内如需改动，先划掉原来答案，然后再写上新答案，严禁使用涂改液、胶带纸、修正带修改，不允许使用计算器．
4．保证答题卡清洁、完整，严禁折叠，严禁在答题卡上做任何标记．
5．评分以答题卡上的答案为依据，不按以上要求作答的答案无效．
一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 若实数a的相反数是﹣1，则a+1等于（ ）
A. 2B. ﹣2C. 0D.
【答案】A
【解析】
【分析】根据相反数的定义即可求解．
【详解】解：∵1的相反数是﹣1，
∴a＝1，
∴a+1=2
故选：A．
【点睛】本题主要考查了相反数，熟记相反数的定义是解题的关键．
2. 下列图案中，既是轴对称图形又是中心对称图形的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据中心对称图形与轴对称图形的概念，把一个图形绕某一点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，进行判断即可．
【详解】解：A．不是中心对称图形，也不是轴对称图形，故此选项不合题意；
B．不是中心对称图形，是轴对称图形，故此选项不合题意；
C．不是中心对称图形，是轴对称图形，故此选项不合题意；
D．既是轴对称图形，又是中心对称图形，故此选项符合题意；
故选：D．
【点睛】本题考查的是中心对称图形与轴对称图形的概念，正确掌握相关定义是解题关键．
3. 经过折叠可以围成正方体，且在正方体侧面上的字恰好环绕组成一个四字成语的图形是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据正方体侧面上的字恰好环绕组成一个四字成语，即是正方体的表面展开图，相对的面之间一定相隔一个正方形，且有两组相对的面，根据这一特点作答．
【详解】解∶由正方体的表面展开图，相对的面之间一定相隔一个正方形可知，
A.“心”、“想”、“事”、“成”四个字没有相对的面，故不符合题意；
B.“吉”、“祥”、“如”、“意”四个字没有相对的面，故不符合题意；
C.“金”与“题”相对，“榜”、“名”是相对的面，故符合题意；
D.“马”、“到”、“成”、“功”四个字没有相对的面，故不符合题意；
故选∶C．
【点睛】本题主要考查了正方体相对两个面上的文字，明确正方体的表面展开图，相对的面之间一定相隔一个正方形是解题的关键．
4. 小红在“养成阅读习惯，快乐阅读，健康成长”读书大赛活动中，随机调查了本校初二年级20名同学，在近5个月内每人阅读课外书的数量，数据如下表所示：
则阅读课外书数量的中位数和众数分别是（ ）
A. 13，15B. 14，15C. 13，18D. 15，15
【答案】D
【解析】
【分析】利用中位数，众数的定义即可解决问题．
【详解】解：中位数为第10个和第11个的平均数，众数为15．
故选：D．
【点睛】本题考查了中位数和众数，解题的关键是掌握平均数、中位数和众数的概念．
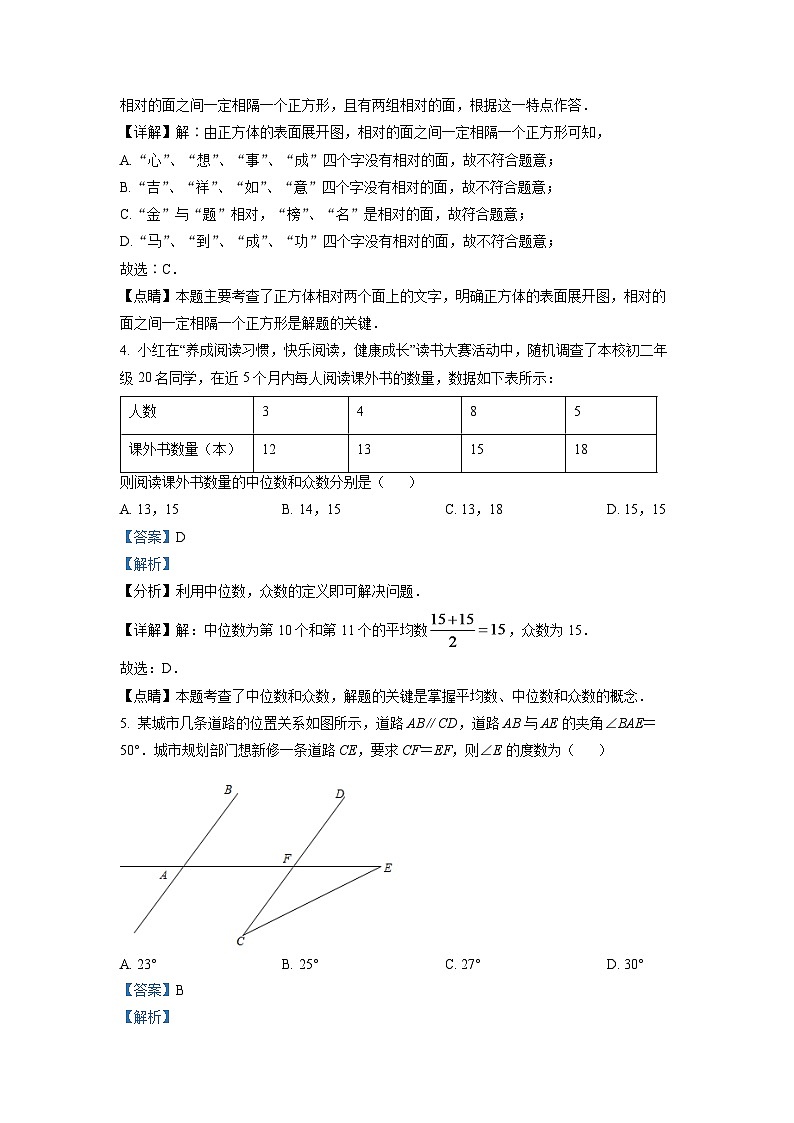
5. 某城市几条道路的位置关系如图所示，道路AB∥CD，道路AB与AE的夹角∠BAE＝50°．城市规划部门想新修一条道路CE，要求CF＝EF，则∠E的度数为（ ）
A. 23°B. 25°C. 27°D. 30°
【答案】B
【解析】
【分析】先根据平行线的性质，由得到∠BAE=∠DFE=50°，然后根据三角形外角性质计算∠E的度数．
【详解】解：∵，∠BAE＝50°，
∴∠BAE=∠DFE=50°，
∵CF＝EF，
∴∠C=∠E，
∵∠DFE=∠C+∠E=50°，
∴∠E=25°．
故选：B．
【点睛】本题考查了平行线的性质，等腰三角形的性质，以及三角形的外角性质，熟练掌握平行线的性质是解题的关键．
6. 下列分数中，和π最接近的是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】把分数化小数，用分数的分子除以分母即得小数商，除不尽时通常保留三位小数，据此先分别把每个选项中的分数化成小数，进而比较得解
【详解】A. ;
B ;
C. ;
D. ;
因为
故和π最接近的是，
故选择:A
【点睛】本题主要考查有理数大小的比较，熟练掌握分数化为小数的方法是解题的关键
7. 如图，在△ABC中，AB=AC，∠A=120°．分别以点A和C为圆心，以大于AC的长度为半径作弧，两弧相交于点P和点Q，作直线PQ分别交BC，AC于点D和点E．若CD=3，则BD的长为（ ）
A. 4B. 5C. 6D. 7
【答案】C
【解析】
【分析】连接AD，由作图知：DE是线段AC的垂直平分线，得到AD=CD=3，∠DAC=∠C=30°，求得∠BAD=90°，再利用含30度角的直角三角形的性质即可求解．
【详解】解：连接AD，
由作图知：DE是线段AC的垂直平分线，
∴AD=CD=3，
∴∠DAC=∠C，
∵AB=AC，∠A=120°，
∴∠B=∠C=30°，则∠DAC=∠C=30°，
∴∠BAD=120°-∠DAC=90°，
∴BD=2AD=6，
故选：C．
【点睛】本题考查了作图-基本作图：熟练掌握5种基本作图是解决问题的关键．也考查了线段垂直平分线的性质，等腰三角形的性质，含30度角的直角三角形的性质．
8. 计算的结果是（ ）
A. ﹣7a6b2B. ﹣5a6b2C. a6b2D. 7a6b2
【答案】C
【解析】
【分析】先根据积的乘方法则计算，再合并同类项．
【详解】解：原式，
故选：C．
【点睛】本题主要考查了积的乘方，合并同类项，解题的关键是掌握相应的运算法则．
9. 为扎实推进“五育”并举工作，加强劳动教育，某校投入2万元购进了一批劳动工具．开展课后服务后，学生的劳动实践需求明显增强，需再次采购一批相同的劳动工具，已知采购数量与第一次相同，但采购单价比第一次降低10元，总费用降低了15%．设第二次采购单价为x元，则下列方程中正确的是（ ）
A.
B.
C.
D.
【答案】D
【解析】
【分析】设第二次采购单价为x元，则第一次采购单价为(x+10)元，根据单价=总价÷数量，结合总费用降低了15%，采购数量与第一次相同，即可得出关于x的分式方程．
【详解】解：设第二次采购单价为x元，则第一次采购单价为(x+10)元，
依题意得：，
故选：D．
【点睛】本题考查了由实际问题抽象出分式方程，找到关键描述语，找到合适的等量关系是解决问题的关键．
10. 如图，在边长为4的菱形ABCD中，E为AD边的中点，连接CE交对角线BD于点F．若∠DEF＝∠DFE，则这个菱形的面积为（ ）
A. 16B. 6C. 12D. 30
【答案】B
【解析】
【分析】连接AC交BD于O，如图，根据菱形的性质得到，CB＝CD＝AD＝4，AC⊥AB，BO＝OD，OC＝AO，再利用∠DEF＝∠DFE得到DF＝DE＝2，证明∠BCF＝∠BFC得到BF＝BC＝4，则BD＝6，所以OB＝OD＝3，接着利用勾股定理计算出OC，从而得到AC＝，然后根据菱形的面积公式计算它的面积．
【详解】解：连接AC交BD于O，如图，
∵四边形ABCD为菱形，
∴，CB＝CD＝AD＝4，AC⊥AB，BO＝OD，OC＝AO，
∵E为AD边中点，
∴DE＝2，
∵∠DEF＝∠DFE，
∴DF＝DE＝2，
∵，
∴∠DEF＝∠BCF，
∵∠DFE＝∠BFC，
∴∠BCF＝∠BFC，
∴BF＝BC＝4，
∴BD＝BF+DF＝4+2＝6，
∴OB＝OD＝3，
在Rt△BOC中，，
∴AC＝2OC＝，
∴菱形ABCD的面积＝AC•BD＝．
故选：B．
【点睛】本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形面积＝ab（a、b是两条对角线的长度）．
11. 若二次函数的图象经过P（1，3），Q（m，n）两点，则代数式的最小值为（ ）
A. 1B. 2C. 3D. 4
【答案】A
【解析】
【分析】先求得a=1，推出，原式化简得，利用偶次方的非负性，即可求解．
【详解】解：∵二次函数的图象经过P（1，3），
∴，
∴a=1，
∴二次函数的解析式为，
∵二次函数的图象经过Q（m，n），
∴即，
∴
，
∵，
∴的最小值为1，
故选：A．
【点睛】本题考查了配方法的应用，待定系数法求二次函数的解析式，二次函数的性质，非负数的性质，利用待定系数法求得二次函数的解析式是解题的关键．
12. 如图，在△ABC中，AB＝AC，点D在AC边上，过△ABD的内心I作IE⊥BD于点E．若BD＝10，CD＝4，则BE的长为（ ）
A. 6B. 7C. 8D. 9
【答案】B
【解析】
【分析】过点作，根据切线长定理设，进而结合已知条件表示出，求得的长，进而即可求解．
【详解】解：如图，过点作，
∵是的内心，
∴，
设，
∵BD＝10，
∴，
∴,，
∵，
∴，
解得，
∴，
故选B．
【点睛】本题考查了三角形内心的性质，切线长定理，掌握切线长定理是解题的关键．
二、填空题：本大题共5个小题，每小题4分，共20分．请直接填写最后结果．
13. 要使式子有意义，则的取值范围是________．
【答案】
【解析】
【分析】根据，二次根式有意义，则被开方数是非负数，即可．
【详解】∵式子有意义
∴
∴
故答案为：．
【点睛】本题考查二次根式的知识，解题的关键是掌握二次根式有意义，则被开方数是非负数，．
14. 分解因式：=____.
【答案】
【解析】
【分析】先提取公因式后继续应用平方差公式分解即可．
【详解】．
故答案为：
15. 如图，在平面直角坐标系中，平移△ABC至△A1B1C1的位置．若顶点A（﹣3，4）的对应点是A1（2，5），则点B（﹣4，2）的对应点B1的坐标是________．
【答案】（1，3）
【解析】
【分析】根据点A和点的坐标可得出平移规律，从而进一步可得出结论．
【详解】解：∵顶点A（﹣3，4）的对应点是A1（2，5），
又
∴平移至的规律为：将向右平移5个单位，再向上平移1个单位即可得到
∵B（﹣4，2）
∴的坐标是（-4+5，2+1），即（1，3）
故答案为：（1，3）
【点睛】本题主要考查了坐标与图形，正确找出平移规律是解答本题的关键．
16. 计算的结果为________．
【答案】﹣2
【解析】
【分析】先变形，再根据同分母分式的加减法进行化简即可．
【详解】解：
=
=
=﹣2，
故答案为：﹣2．
【点睛】本题考查分式的加减，灵活运用分式的加减运算法则是解答的关键．
17. 如图，正方形ABCD的中心与坐标原点O重合，将顶点D（1，0）绕点A（0，1）逆时针旋转90°得点D1，再将D1绕点B逆时针旋转90°得点D2，再将D2绕点C逆时针旋转90°得点D3，再将D3绕点D逆时针旋转90°得点D4，再将D4绕点A逆时针旋转90°得点D5……依此类推，则点D2022的坐标是________．
【答案】（-2023，2022）
【解析】
【分析】由题意观察发现：每四个点一个循环，，由，推出．
【详解】解：将顶点绕点逆时针旋转得点，
，
再将绕点逆时针旋转得点，再将绕点逆时针旋转得点，再将绕点逆时针旋转得点，再将绕点逆时针旋转得点
，，，，，，
观察发现：每四个点一个循环，，
，
；
故答案为：．
【点睛】本题考查坐标与图形的变化旋转，等腰直角三角形性质，规律型问题，解题的关键是学会探究规律的方法，找到规律再利用规律求解．
三、解答题：本大题共7个小题，共70分．解答要写出必要的文字说明，证明过程或演算步骤．
18. 解方程组：
【答案】
【解析】
【分析】整理方程组得，继而根据加减消元法解二元一次方程组即可求解．
【详解】解：整理方程组得，
得，
y=1，
把y=1代入①得，
解得x=5，
∴方程组的解为.
【点睛】本题考查了解二元一次方程组，正确的计算是解题的关键．
19. 如图，△ABC是等腰三角形，点D，E分别在腰AC，AB上，且BE＝CD，连接BD，CE．求证：BD＝CE．
【答案】证明见解析
【解析】
【分析】根据等腰三角形的性质得出，进而利用证明与全等，再利用全等三角形的性质解答即可．
【详解】证明：是等腰三角形，
，
在与中，
，
，
．
【点睛】此题考查全等三角形的判定和性质，解题的关键是利用证明与全等．
20. 如图，直线y=kx+b与双曲线y=相交于A（1，2），B两点，与x轴相交于点C（4，0）．
（1）分别求直线AC和双曲线对应的函数表达式；
（2）连接OA，OB，求△AOB的面积；
（3）直接写出当x＞0时，关于x的不等式kx+b＞的解集．
【答案】（1）y=x+，y=；
（2）△AOB的面积为；
（3）1