

山东省淄博第七中学2024-2025学年高一上学期12月月考 数学试卷(含解析)
展开
这是一份山东省淄博第七中学2024-2025学年高一上学期12月月考 数学试卷(含解析),共16页。试卷主要包含了本试卷分选择题和非选择题两部分, 函数的图象大致为, 已知,若,则等内容,欢迎下载使用。
1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
2.答题前,考生将自己的姓名、准考证号填写在答题卡指定位置上
3.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写.
4.请按题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.
一、单项选择题:本大题共8小题每小题5分,共40分.在每小题给出的四个选项中,只有一项是正确的,请把正确的选项填涂在答题卡相应的位置上.
1. 已知集合,,则( )
A. B. C. D.
【答案】C
解析:∵,,
∴.
故选:C.
2. 已知命题,,则是( )
A. ,B. ,
C. ,D. ,
【答案】B
解析:命题,,则:,.
故选:B
3. 函数的定义域是( )
A. B. C. D.
【答案】C
解析:因为,所以,解得,
所以函数的定义域是.
故选:C.
4. 若函数的一个正数零点附近的函数值用二分法逐次计算,参考数据如表:那么方程的一个近似根(精确度0.04)为( )
A. 1.5B. 1.25C. 1.375D.
【答案】D
解析:由表格可知,方程的近似根在内,
又因为,又,
故方程的一个近似根(精确度)可以为.
故选:D.
5. 设m,n为实数,则“”是“”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【答案】A
解析:因为函数为上的单调递增函数,又,所以,所以,又函数在上单调递减,所以,所以“”是“”的充分条件,因为函数在上单调递减,又,所以,当为负数时,没有对数值,所以“”不是“”的必要条件,所以“”是“”的充分不必要条件,A正确,
故选:A.
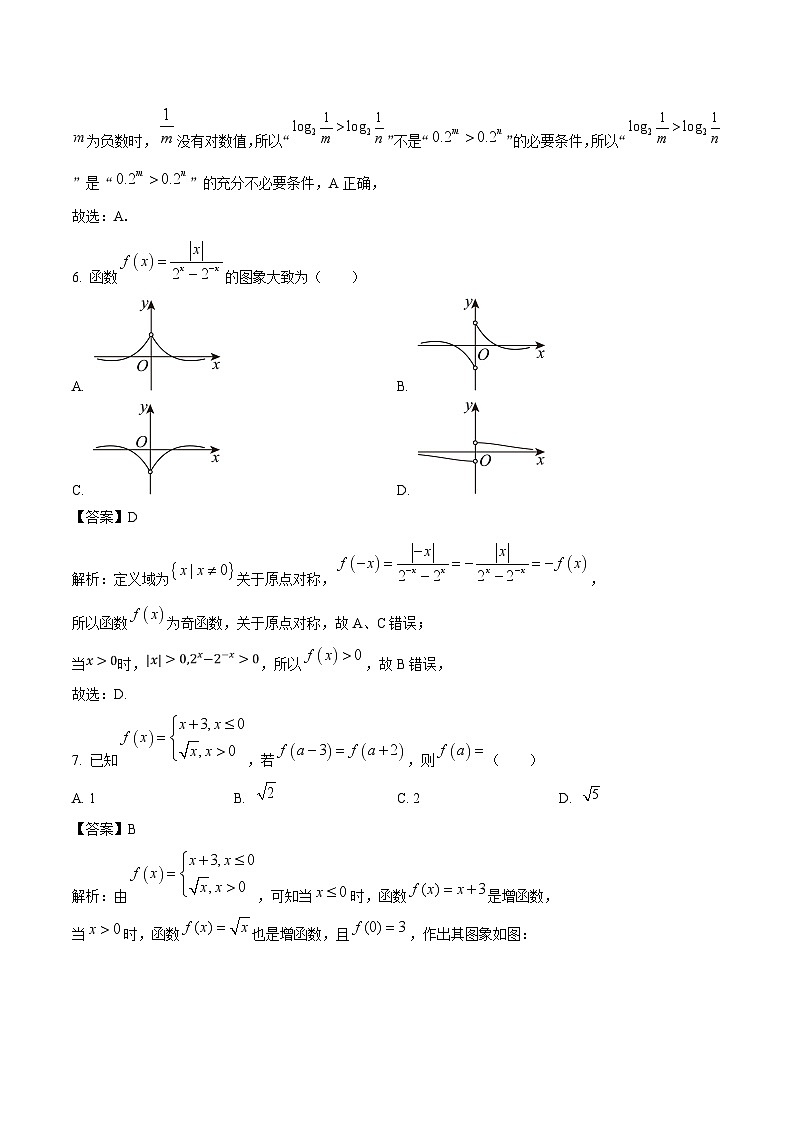
6. 函数的图象大致为( )
A. B.
C. D.
【答案】D
解析:定义域为关于原点对称,,
所以函数为奇函数,关于原点对称,故A、C错误;
当时,,所以,故B错误,
故选:D.
7. 已知,若,则( )
A. 1B. C. 2D.
【答案】B
解析:由,可知当时,函数是增函数,
当时,函数也是增函数,且,作出其图象如图:
因,且,则,
故得,解得或,
由知,故,则.
故选:B.
8. 已知函数,设,,,则a,b,c的大小关系是( )
A. B. C. D.
【答案】C
解析:函数,由得 ,故,解得.
∵,∴为偶函数,故.
当时,,
∵在上为减函数,且,∴在上为增函数,
∴在上为增函数,在上为减函数.
∵,,,
∴,
∴,即.
故选:C.
二、多项选择题:本题共3小题,每题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得6分,选对但不全对得部分分,有选错的得0分.
9. 已知正实数满足,下列结论中正确的是( )
A. 的最大值是B. 的最小值是
C. 的最小值是3D. 的最小值为
【答案】BCD
解析:解:对于A项:因为,所以,
则(当且仅当时取等号),故A错误;
对于B项:因为(当且仅当时取等号),故B正确;
对于C项:因为,所以,
因为,
所以(当且仅当时取等号),故C正确;
对于D项:(当且仅当时取等号),故D正确.
故选:BCD.
10. 给出下列结论,其中不正确的结论是( )
A. 函数最大值为
B. 已知函数且在上是减函数,则实数的取值范围是
C. 在同一平面直角坐标系中,函数与的图象关于直线对称
D. 已知定义在上的奇函数在内有110个零点,则函数的零点个数为221
【答案】AB
解析:对A选项,利用复合函数的单调性,令,随增大函数值减小,
而当时,有最大值,可求得当时,的最小值为,可知A选项错误;
对B选项,可令,
当时,中,随增大而减小,若原函数是减函数,则随增大而增大,
可得,与条件矛盾;
当时,随减小而减小,且真数要恒大于0,
满足题意的不等式组为,可知的取值范围为,B选项错误;
对C选项,设的图像上任意一点,将指数式转化为对数式:,可知其关于的对称点在的图像上,
反之,对于的图像上的任意一点,将对数式转化为指数式,有,即点关于直线的对称点在函数的图像上,
可知的图像与的图像关于对称,C选项正确;
(也可根据同一底数的指数函数和对数函数互为反函数,互为反函数的函数图像关于对称判断);
对于D选项,奇函数的图像关于原点中心对称,在有个零点,则在也有个零点,再加上定义在上的奇函数图像必过原点,也是一个零点,共有个零点,D选项正确.
故选:AB
11. 已知函数,则( )
A. 是R上的减函数 B. 不等式的解集为
C. 若是奇函数,则D. 的图象关于点对称
【答案】ABC
解析:A选项,在R上单调递增,且恒成立,
故是R上的减函数,A正确;
B选项,,
故,所以,
由A知,是R上的减函数,故,解得,
故等式的解集为,B正确;
C选项,若是奇函数,则,
由B选项知,,故,解得,C正确;
D选项,由B选项知,,故的图象关于点对称,
由于与不一定是同一个点,D错误.
故选:ABC
三、填空题:本题共3小题,每题5分,共15分
12. ______.
【答案】
解析:原式,
故答案为:.
13. 幂函数在上单调递增,则的图像过定点______.
【答案】
解析:由题意得且,解得或-1(舍去),
故,令,得,此时,
故的图象过定点.
故答案为:
14. 设函数,若函数的零点为4,则使得成立的整数t的个数为______.
【答案】10
解析:由题意得,故,
又,所以,
解得,
所以,定义域为,
由于在上单调递减,在上单调递增,
故在上单调递减,
且,
由得,
即,所以,
解得,
又为整数,故,
故使得成立的整数t的个数为10.
故答案为:10
四、解答题:本题共5小题,共77分.解答应写出必要的文字说明,证明过程或演算步骤.
15. 已知集合,.
(1)若,,求;
(2)若,求正数a的取值范围.
【答案】(1)或; (2)
(1)
,故,解得,
又,故,则,
或;
(2)
,故,解得,
故,
因为,所以,
故,
因为,所以,解得,
所以正数a的取值范围是.
16. 已知(,且),且.
(1)求a的值及的定义域;
(2)求在上的最小值.
【答案】(1),
(2)
(1)
,即,则,
由题意得,∴,的定义域为:.
(2)
,
令,则,
的对称轴:,
∴在上单调递增,在上单调递减;
∵,∴在单调递减,
由复合函数可知:时,单调递减,时,单调递增,
∴.
17. 已知函数为奇函数.
(1)求的值;
(2)判断并证明的单调性;
(3)若不等式对任意都成立,求实数的取值范围.
【答案】(1)1; (2)在R上单调递减,证明见解析;
(3).
(1)
由函数为奇函数,其定义域为,
所以,
即,解得,此时,
满足,
即为奇函数,
故值为.
(2)
解:在R上单调递减,证明如下:
由(1)知,
,且,
则,
因为,所以,,,
所以,,
即函数在上单调递减;
(3)
由题知:当恒成立;
则;
令,
所以;
又,当且仅当时等号成立,
而,所以,则.
所以实数的取值范围为
18. 学校为了鼓励学生课余时间积极参加体育锻炼,需要制定一个课余锻炼考核评分制度,建立一个每天得分与当天锻炼时间(单位:分钟,)的函数关系式,要求如下:
(i)函数的图象接近图示;
(ii)每天锻炼时间为0分钟时,当天得分为0分;
(iii)每天锻炼时间为9分钟时,当天得分为6分;
(iiii)每天得分最多不超过12分.
现有以下三个函数模型供选择:
①;②;③.
(1)请根据函数图像性质,结合题设条件,从中选择一个最合适的函数模型并求出解析式;
(2)若学校要求每天的得分不少于9分,求每天至少锻炼多少分钟?
(参考值:)
【答案】(1)选择③,;
(2)29.25.
(1)
模型①,由图象过点,
得,解得, ,在原点附近增长速度先快后慢,不符合;
模型②为爆炸增长型函数,不符合,
故选模型③.
由题知,,解得,
所以.
(2)
由(1)知,,
令,得,解得,
所以,若每天的得分不少于9分,至少每天要锻炼29.25分钟.
19. “函数的图像关于点对称”的充要条件是“对于函数定义域内的任意x,都有”.若函数的图像关于点对称,且当时,.
(1)求的值;
(2)设函数
(ⅰ)证明:函数的图像关于点对称;
(ⅱ)若对任意,总存在,使得成立,求实数a的取值范围.
【答案】(1)4; (2)(ⅰ)证明过程见解析;(ⅱ).
(1)
函数的图像关于点对称,
故,
令得;
(2)
(ⅰ)证明:,
故,
故函数的图像关于点对称;
(ⅱ),
故在上单调递增,其中,
,
故的值域为,
设在上的值域为,由题意得,
图象开口向上,对称轴为,且,
当时,
若,即,函数在上单调递增,
由对称性可知,在上单调递增,故在上单调递增,
因为,所以,
所以,由得,解得,
当,即时,在上单调递减,在上单调递增,
由对称性可知,在上单调递增,在上单调递减,
所以在上单调递减,在上单调递增,在上单调递减,
结合对称性可知,或,
因为,所以,
,
又,
所以,
所以当时,满足;
当,即时,在上单调递减,
由对称性可知,在上单调递减,故在上单调递减,
因为,所以,
所以,由得,解得,
综上,的取值范围为.
相关试卷
这是一份2024-2025学年山东省淄博市高一上册12月月考数学检测试卷(含解析),共16页。试卷主要包含了本试卷分选择题和非选择题两部分, 函数的图象大致为, 已知,若,则等内容,欢迎下载使用。
这是一份山东省淄博市淄博中学2024-2025学年高一上学期12月月考数学试卷,共8页。
这是一份山东省淄博中学2024-2025学年高一上学期期中考试数学试卷,共1页。








