初中数学湘教版（2024）七年级下册（2024）3.3 一元一次不等式的解法公开课课件ppt

这是一份初中数学湘教版（2024）七年级下册（2024）3.3 一元一次不等式的解法公开课课件ppt，文件包含新湘教版初中数学七年级下册331《一元一次不等式的解法》课件pptx、新湘教版初中数学七年级下册331《一元一次不等式的解法》教案docx等2份课件配套教学资源，其中PPT共18页， 欢迎下载使用。
1.理解掌握一元一次不等式的相关概念，能熟练解一元一次不等式，并能在数轴上表示一元一次不等式的解集。
理解掌握一元一次不等式解法，及在数轴上表示它的解集的方法和技巧。
一元一次不等式的解法及在数轴上表示它的解集的方法和技巧。
2.通过利用不等式的基本性质对不等式的变形，引出对一元一次不等式的学习，并将解一元一次不等式与解一元一次方程进行比较，以加深对解一元一次不等式掌握。
3. 培养学生的观察比较能力，实际操作能力，数形结合能力。学习所需的数学知识和技能，激发学生学习数学的兴趣。
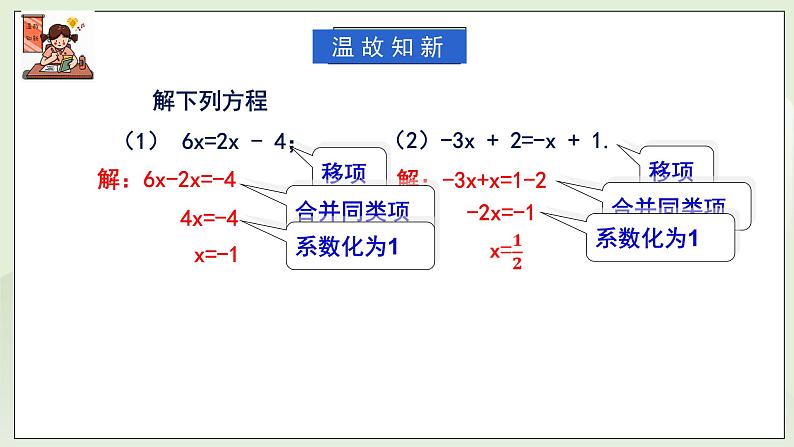
（1） 6x=2x - 4；
（2）-3x + 2=-x + 1.
解：-3x+x=1-2
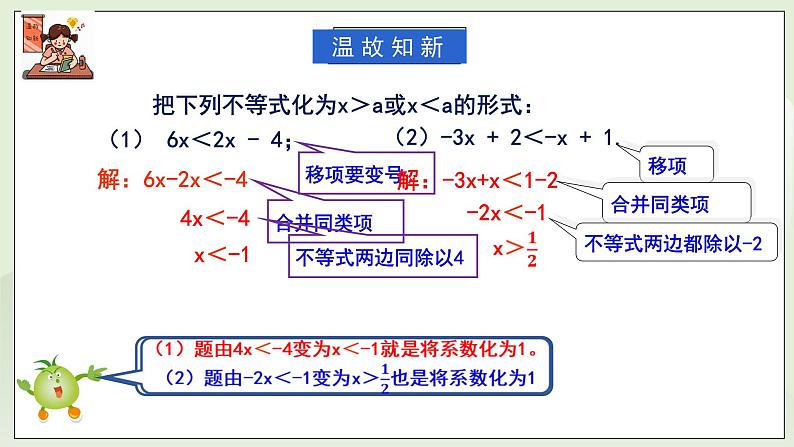
把下列不等式化为x＞a或x＜a的形式：
（1） 6x＜2x - 4；
不等式两边同除以4
（2）-3x + 2＜-x + 1.
解：-3x+x＜1-2
当x=-1.5时，代入（1）中，
左边=-9，右边=-7，左边＜右边，不等式成立。
当x=-2时，代入（1）中，
左边=-12，右边=-8，左边＜右边，不等式成立。
当x=-3时，代入（1）中，
左边=-18，右边=-10，左边＜右边，不等式成立。
只要符合x＜-1的数代入（1）中，不等式都成立。
含有一个未知数，且含未知数的项的次数是1的不等式，称为一元一次不等式.
对于一个未知数为x的一元一次不等式，如果未知数x实数a代入，能够使得不等式成立，那么a称为这个不等式的一个解.
我们把这个不等式的解的全体称为这个不等式的解集.
例如 我们用x＜-1表示6x＜2x - 4的解集.
解下列一元一次不等式.
数轴表示不等式的解集
一个不等式的解集常常可以借助数轴直观地表示出来.
则点A右边所有的点表示的数都大于2，而点A左边所有的点表示的数都小于2。
1、找出分界点：能够等于是实心点；不能等于是空心点。
2、画方向线：方向线与不等号小尖方向一致。
例1 解不等式12-6x≥2(1-2x)，并把它的解集在数轴上表示出来 ：
两边都除以-2，得:
∴原不等式的解集在数轴上表示如下：
-6x+4x≥2-12
解集x≤5中包括5，所以在数轴上将表示5的分界点画成实心圆点
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点？
它们的步骤基本相同，都是去分母、去括号、移项、合并同类项、两边都除以未知数的系数.
它们的依据不相同.解一元一次方程的依据是等式的性质；解一元一次不等式的依据是不等式的性质.
这些步骤中，要特别注意的是：不等式两边都乘（或除以）同一个负数，必须改变不等号的方向.这是与解一元一次方程不同的地方.
解下列不等式，并把它们的解集在数轴上表示出来：
（1）-5x ≤ 10；
（2） 10x + 7＜ 4x + 1；
解：10x-4x＜1-7
（3） 3x-12＞2（1+ 4x）；
（4） 3（5x + 4）≥ 7x + 8.
解：3x-12＞2+8x
解：15x+12≥ 7x + 8
15x-7x≥8-12
练 习
设a是实数，如果不等式（a+1）x＞a + 1的解集是x＜1，那么a应满足什么条件？
解：∵（a+1）x＞a + 1的解集是x＜1
∴原不等式两边同除以负数（a+1)，即：a+1＜0
不等号的方向改变，是因为不等式两边同除以一个负数（a+1)
一元一次不等式的概念：
含有一个未知数，且含未知数的项的次数是1的不等式。
一元一次不等式的解集:
满足一元一次不等式的未知数的每一个值。
一元一次不等式的解的全体称。
x≤a(或x＜a，x＞a，x≥a）
解一元一次不等式的步骤：
解一元一次不等式的步骤与解方程相同。
数轴表示不等式的解集：
①分界点：包括分界点是实心点；不包括分界点是空心点。
②方向线：方向线与不等号小尖方向一致。
课堂作业：P70习题3.3第1题;
课后作业：P81复习题3第4、5题，并预习P68~69《解不等式》。