2025中考数学一轮复习讲练 第23讲 四边形（含解析+考点卡片）

这是一份2025中考数学一轮复习讲练 第23讲 四边形（含解析+考点卡片），共37页。试卷主要包含了学会运用函数与方程思想，学会运用数形结合思想，要学会抢得分点，学会运用等价转换思想，学会运用分类讨论的思想，转化思想等内容，欢迎下载使用。
2、学会运用数形结合思想。数形结合思想是指从几何直观的角度,利用几何图形的性质研究数量关系，寻求代数问题的解决方法（以形助数）。
3、要学会抢得分点。要将整道题目解题思路转化为得分点。
4、学会运用等价转换思想。将抽象的问题转化为具体的问题，将实际问题转化为数学问题。
5、学会运用分类讨论的思想。纵观近几年的中考压轴题分类讨论思想解题已成为新的热点。
6、转化思想：体现在数学上也就是要把难转简，把不熟转熟，把未知转为已知的问题。
2025年中考数学一轮复习
第23讲 四边形
一．选择题（共10小题）
1．如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F，若∠BAF＝90°，BC＝5，EF＝3，则CD的长是（ ）
A．6B．8C．10D．12
2．如图，在平面直角坐标系中，点A，B在第一象限，点C在x轴正半轴上，且AC与OB互相垂直平分，D为垂足，连接OA，AB，BC．反比例函数y=kx(x＞0)的图象经过点D，与OA相交于E．若点B的坐标为（8，4），则点E的坐标是（ ）
A．(2，432)B．(143，343)C．(145，345)D．(6，436)
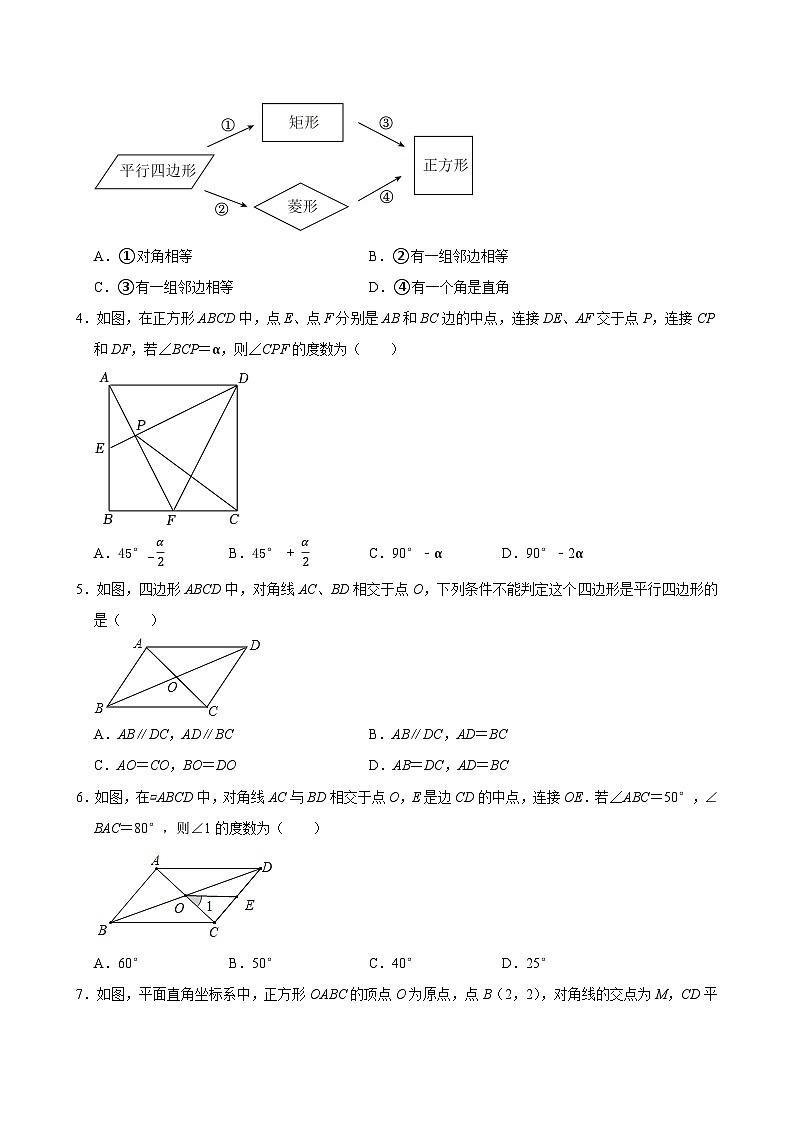
3．在复习特殊的平行四边形时，某小组同学画出了如下关系图，组内一名同学在箭头处填写了它们之间转换的条件，其中填写错误的是（ ）
A．①对角相等B．②有一组邻边相等
C．③有一组邻边相等D．④有一个角是直角
4．如图，在正方形ABCD中，点E、点F分别是AB和BC边的中点，连接DE、AF交于点P，连接CP和DF，若∠BCP＝α，则∠CPF的度数为（ ）
A．45°−α2B．45°+α2C．90°﹣αD．90°﹣2α
5．如图，四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（ ）
A．AB∥DC，AD∥BCB．AB∥DC，AD＝BC
C．AO＝CO，BO＝DOD．AB＝DC，AD＝BC
6．如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连接OE．若∠ABC＝50°，∠BAC＝80°，则∠1的度数为（ ）
A．60°B．50°C．40°D．25°
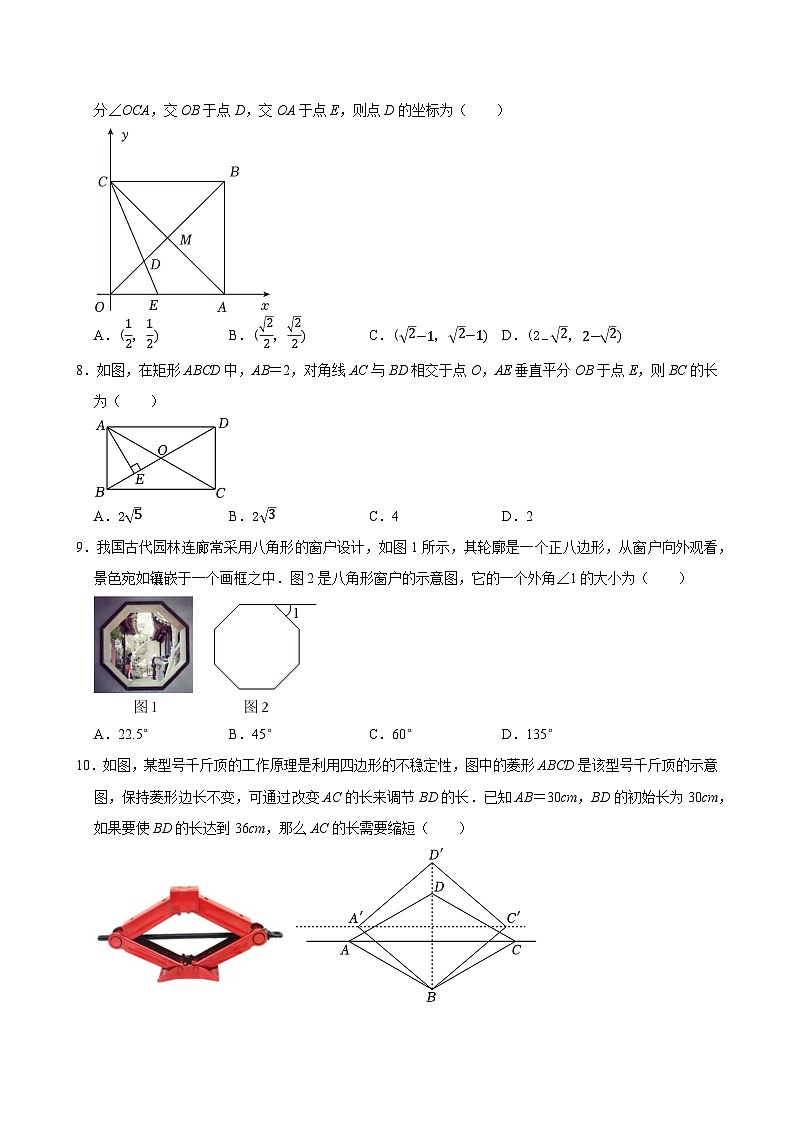
7．如图，平面直角坐标系中，正方形OABC的顶点O为原点，点B（2，2），对角线的交点为M，CD平分∠OCA，交OB于点D，交OA于点E，则点D的坐标为（ ）
A．(12，12)B．(22，22)C．(2−1，2−1)D．(2−2，2−2)
8．如图，在矩形ABCD中，AB＝2，对角线AC与BD相交于点O，AE垂直平分OB于点E，则BC的长为（ ）
A．25B．23C．4D．2
9．我国古代园林连廊常采用八角形的窗户设计，如图1所示，其轮廓是一个正八边形，从窗户向外观看，景色宛如镶嵌于一个画框之中．图2是八角形窗户的示意图，它的一个外角∠1的大小为（ ）
A．22.5°B．45°C．60°D．135°
10．如图，某型号千斤顶的工作原理是利用四边形的不稳定性，图中的菱形ABCD是该型号千斤顶的示意图，保持菱形边长不变，可通过改变AC的长来调节BD的长．已知AB＝30cm，BD的初始长为30cm，如果要使BD的长达到36cm，那么AC的长需要缩短（ ）
A．6cmB．8cm
C．(303−36)cmD．(303−48)cm
二．填空题（共5小题）
11．如图，在矩形ABCD中，AD＝5，DC＝7，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，DH＝3，连接CF．当△FCG的面积为5时，DG的长为 ．
12．如图，正八边形ABCDEFGH的对角线AF，HD交于点M，则∠AMH的度数是 °．
13．如图，在正方形ABCD中，点E为CD上靠近点D的三等分点，点F为BC的中点，以EF为直角边，点E为直角顶点向右构造等腰Rt△EFG，连接AG、CG，则AGCG的值为 ．
14．如图，在矩形ABCD中，AB＝6，AD＝12，E是线段AD上一动点，以E为直角顶点在EB的右侧作等腰三角形EBF，连接DF，当点F落在矩形ABCD的对角线上时，则DF的长为 ．
15．如图是由6个形状、大小完全相同的菱形组成的网格，菱形的顶点称为格点，已知菱形的一个角（∠O）为60°，点A，B，C都在格点上，则sin∠ABC的值是 ．
三．解答题（共5小题）
16．如图，在矩形ABCD中，E为AB边上一点，EC平分∠DEB，F为CE的中点，连接AF，BF，过点E作EH∥BC分别交AF，CD于G，H两点．
（1）求证：AB＝DE；
（2）请判断AF，BF的位置关系，并说明理由．
17．如图，BD平分∠ABF，点A是射线BM上一点，过点A作AD∥BN交BG于点D，过A作AE⊥BN，过点D作DF⊥BN．
（1）求证：四边形AEFD是矩形；
（2）在BF上取点C使得CF＝BE，连接AC、CD．求证：AC⊥BD．
18．如图，在▱ABCD中，AE⊥BC于点E，延长BC至点F，使CF＝BE，连接DF，AF与DE交于点O．
（1）求证：四边形AEFD为矩形；
（2）若AB＝3，OE＝2，BF＝5，求DF的长．
19．如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB，交AB的延长线于点E，连接OE．
（1）求证：四边形ABCD是菱形．
（2）若AB＝5，BD＝6，求OE的长．
20．如图，在矩形ABCD中，点F是BC上一点，且CF＝2BF，CE⊥AF，垂足为点E，∠BCE＝30°．
（1）求证：AE＝EF+CF；
（2）若AD＝6cm，点P是AD上一动点，以1cm/s的速度从点A运动到点D，问：点P运动多少秒四边形AFCP是菱形？请说明理由．
2025年中考数学一轮复习
第23讲 四边形
一．选择题（共10小题）
1．如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F，若∠BAF＝90°，BC＝5，EF＝3，则CD的长是（ ）
A．6B．8C．10D．12
【考点】平行四边形的性质．
【专题】图形的全等；等腰三角形与直角三角形；多边形与平行四边形；运算能力；推理能力．
【答案】B
【分析】由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE＝∠F，∠D＝∠ECF，由全等三角形的性质得出AE＝EF＝3，由平行线的性质证出∠AED＝∠BAF＝90°，求出DE，即可得出CD的长．
【解答】解：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，
∴∠DAE＝∠F，∠D＝∠ECF，
∵E是▱ABCD的边CD的中点，
∴DE＝CE，
在△ADE和△FCE中，
∠DAE=∠F∠D=∠ECFDE=CE，
∴△ADE≌△FCE（AAS），
∴AE＝EF＝3，
∵AB∥CD，
∴∠AED＝∠BAF＝90°，
在△ADE中，AD＝BC＝5，
∴DE=AD2−AE2=52−32=4，
∴CD＝2DE＝8．
故选：B．
【点评】此题考查了平行四边形的性质、全等三角形的判定方法、勾股定理；熟练掌握平行四边形的性质，证明三角形全等是解决问题的关键．
2．如图，在平面直角坐标系中，点A，B在第一象限，点C在x轴正半轴上，且AC与OB互相垂直平分，D为垂足，连接OA，AB，BC．反比例函数y=kx(x＞0)的图象经过点D，与OA相交于E．若点B的坐标为（8，4），则点E的坐标是（ ）
A．(2，432)B．(143，343)C．(145，345)D．(6，436)
【考点】菱形的判定与性质；反比例函数图象上点的坐标特征．
【专题】反比例函数及其应用；矩形 菱形 正方形；应用意识．
【答案】D
【分析】由中点坐标公式可求点D坐标，由反比例函数的性质可求k的值，将各选项坐标代入可求解．
【解答】解：∵AC与OB互相垂直平分，点B的坐标为（8，4），
∴点D的坐标为（4，2），
∴k＝4×2＝8，
∴只有选项D的坐标满足k=6×463=8，
故选：D．
【点评】本题考查了反比例函数图象上点的坐标特征，菱形的性质，灵活运用这些性质解决问题是解题的关键．
3．在复习特殊的平行四边形时，某小组同学画出了如下关系图，组内一名同学在箭头处填写了它们之间转换的条件，其中填写错误的是（ ）
A．①对角相等B．②有一组邻边相等
C．③有一组邻边相等D．④有一个角是直角
【考点】平行四边形的性质．
【专题】多边形与平行四边形；推理能力．
【答案】A
【分析】根据平行四边形的性质和矩形、菱形、正方形的判定定理，对它们之间转换的条件一一进行分析，即可得出结果；
【解答】解：A、①，对角相等的平行四边形，不一定是矩形，故该转换条件填写错误，符合题意；
B、②，有一组邻边相等的平行四边形是菱形，故该转换条件填写正确，不符合题意；
C、③，有一组邻边相等的矩形是正方形，故该转换条件填写正确，不符合题意；
D、④，有一个角是直角的菱形是正方形，故该转换条件填写正确，不符合题意；
故选：A．
【点评】本题考查了平行四边形的性质、矩形和菱形、正方形的判定，解本题的关键在熟练掌握矩形、菱形、正方形的判定定理；
4．如图，在正方形ABCD中，点E、点F分别是AB和BC边的中点，连接DE、AF交于点P，连接CP和DF，若∠BCP＝α，则∠CPF的度数为（ ）
A．45°−α2B．45°+α2C．90°﹣αD．90°﹣2α
【考点】正方形的性质；全等三角形的判定与性质．
【专题】图形的全等；矩形 菱形 正方形；推理能力．
【答案】A
【分析】延长AF，DC交于G，证明△DAE≌△ABF（SAS），可得∠APE＝90°＝∠DPG，再证△ABF≌△GCF（ASA），可得CP为Rt△DPG斜边上的中线，故∠CPF＝∠G，即得∠CPF+∠CPF+（α+90°）＝180°，∠CPF＝45°−α2．
【解答】解：延长AF，DC交于G，如图：
∵四边形ABCD是正方形，
∴AB＝AD＝BC＝CD，∠DAE＝∠B＝90°，
∵E，F是AB，BC的中点，
∴AE=12AB=12BC＝BF，
∴△DAE≌△ABF（SAS），
∴∠ADE＝∠BAF，
∵∠ADE+∠AED＝90°，
∴∠BAF+∠AED＝90°，
∴∠APE＝90°＝∠DPG，
∵∠B＝∠GCF＝90°，BF＝CF，∠AFB＝∠GFC，
∴△ABF≌△GCF（ASA），
∴AB＝CG，
∴CG＝CD，
∴CP为Rt△DPG斜边上的中线，
∴CP=12DG＝CG，
∴∠CPF＝∠G，
∵∠CPF+∠G+∠PCG＝180°，
∴∠CPF+∠CPF+（α+90°）＝180°，
∴∠CPF＝45°−α2；
故选：A．
【点评】本题考查正方形性质及应用，涉及全等三角形判定与性质，解题的关键是作辅助线，构造全等三角形解决问题．
5．如图，四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（ ）
A．AB∥DC，AD∥BCB．AB∥DC，AD＝BC
C．AO＝CO，BO＝DOD．AB＝DC，AD＝BC
【考点】平行四边形的判定．
【答案】B
【分析】利用平行四边形的判定方法：（1）两组对边分别平行的四边形是平行四边形．（2）两组对边分别相等的四边形是平行四边形．（3）一组对边平行且相等的四边形是平行四边形．（4）两组对角分别相等的四边形是平行四边形．（5）对角线互相平分的四边形是平行四边形进行分析即可．
【解答】解：A、AB∥DC，AD∥BC可利用两组对边分别平行的四边形是平行四边形判定这个四边形是平行四边形，故此选项不合题意；
B、AB∥DC，AD＝BC不能判定这个四边形是平行四边形，故此选项符合题意；
C、AO＝CO，BO＝DO可利用对角线互相平分的四边形是平行四边形判定这个四边形是平行四边形，故此选项不合题意；
D、AB＝DC，AD＝BC可利用两组对边分别相等的四边形是平行四边形判定这个四边形是平行四边形，故此选项不合题意；
故选：B．
【点评】此题主要考查了平行四边形的判定，关键是掌握平行四边形的判定定理．
6．如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连接OE．若∠ABC＝50°，∠BAC＝80°，则∠1的度数为（ ）
A．60°B．50°C．40°D．25°
【考点】平行四边形的性质；三角形中位线定理．
【专题】多边形与平行四边形．
【答案】B
【分析】直接利用三角形内角和定理得出∠BCA的度数，再利用三角形中位线定理结合平行线的性质得出答案．
【解答】解：∵∠ABC＝50°，∠BAC＝80°，
∴∠BCA＝180°﹣50°﹣80°＝50°，
∵对角线AC与BD相交于点O，E是边CD的中点，
∴EO是△DBC的中位线，
∴EO∥BC，
∴∠1＝∠ACB＝50°．
故选：B．
【点评】此题主要考查了三角形内角和定理、三角形中位线定理等知识，得出EO是△DBC的中位线是解题关键．
7．如图，平面直角坐标系中，正方形OABC的顶点O为原点，点B（2，2），对角线的交点为M，CD平分∠OCA，交OB于点D，交OA于点E，则点D的坐标为（ ）
A．(12，12)B．(22，22)C．(2−1，2−1)D．(2−2，2−2)
【考点】正方形的性质；相似三角形的判定与性质；坐标与图形性质．
【专题】矩形 菱形 正方形；图形的相似；推理能力．
【答案】D
【分析】过点E作EF⊥AC于点F，过点D作DH⊥OA于点H，延长HD交BC于点G，根据点B的坐标得出正方形的边长，即可求出对角线AC的长，根据角平分线的性质得出OC＝CF，OE＝EF，求出AF的长即可得出OE的长，再根据正方形的性质证得△BCD∽△OED，根据相似三角形对应高之比等于相似比即可求出DH的长，最后根据△DOH为等腰直角三角形即可得出点D的坐标．
【解答】解：过点E作EF⊥AC于点F，过点D作DH⊥OA于点H，延长HD交BC于点G，
∵四边形OABC为正方形，
∴OA＝AB＝BC＝OC，∠OAB＝∠ABC＝∠BCO＝∠COA＝90°，∠OAC＝∠AOB＝45°，BC∥OA，
∵点B（2，2），
∴OA＝AB＝BC＝OC＝2，
由勾股定理得AC=OC2+OA2=22+22=22，
∵CD平分∠OCA，∠COA＝∠EFC＝90°，
∴∠OEC＝∠FEC，OE＝EF，
∴OC＝CF＝2，
∴AF＝AC﹣CF=22−2，
∵∠EFA＝90°，∠OAC＝45°，
∴△AEF是等腰直角三角形，
∴EF＝AF=22−2，
∴OE=22−2，
∵BC∥OA，DH⊥OA，
∴DG⊥BC，
∴DG＝OC＝2，
∵BC∥OA，
∴△BCD∽△OED，
∴BCOE=DGDH，
∴222−2=2−DHDH，
∴DH=2−2，
∵∠AOB＝45°，
∴△ODH是等腰直角三角形，
∴OH=2−2，
∴点D的坐标为(2−2，2−2)，
故选：D．
【点评】本题考查了正方形的性质，相似三角形的判定与性质，角平分线的性质，勾股定理，坐标与图形性质，熟练掌握这些知识点是解题的关键．
8．如图，在矩形ABCD中，AB＝2，对角线AC与BD相交于点O，AE垂直平分OB于点E，则BC的长为（ ）
A．25B．23C．4D．2
【考点】矩形的性质；线段垂直平分线的性质．
【专题】等腰三角形与直角三角形；矩形 菱形 正方形；推理能力．
【答案】B
【分析】由矩形的性质和线段垂直平分线的性质可证△AOB是等边三角形，可得∠BAC＝60°，即可求解．
【解答】解：∵四边形ABCD是矩形，
∴AO＝BO＝CO＝DO，
∵AE垂直平分OB，
∴AB＝AO，
∴AB＝AO＝BO，
∴△AOB是等边三角形，
∴∠BAC＝60°，
∴BC=3AB＝23，
故选：B．
【点评】本题考查了矩形的性质，线段垂直平分线的性质，等边三角形的判定和性质，直角三角形的性质，灵活运用这些性质解决问题是解题的关键．
9．我国古代园林连廊常采用八角形的窗户设计，如图1所示，其轮廓是一个正八边形，从窗户向外观看，景色宛如镶嵌于一个画框之中．图2是八角形窗户的示意图，它的一个外角∠1的大小为（ ）
A．22.5°B．45°C．60°D．135°
【考点】平面镶嵌（密铺）；多边形内角与外角．
【专题】多边形与平行四边形；运算能力．
【答案】B
【分析】由多边形的外角和定理直接可求出结论．
【解答】解：∵正八边形的每一个外角都相等，外角和为360°，
∴它的一个外角∠1＝360°÷8＝45°．
故选：B．
【点评】本题考查了多边形外角和定理，平面镶嵌等知识点，掌握外角和定理是解题的关键．
10．如图，某型号千斤顶的工作原理是利用四边形的不稳定性，图中的菱形ABCD是该型号千斤顶的示意图，保持菱形边长不变，可通过改变AC的长来调节BD的长．已知AB＝30cm，BD的初始长为30cm，如果要使BD的长达到36cm，那么AC的长需要缩短（ ）
A．6cmB．8cm
C．(303−36)cmD．(303−48)cm
【考点】多边形；三角形的稳定性．
【专题】矩形 菱形 正方形；运算能力．
【答案】D
【分析】设AC与BD交于点O，A'C'于BD'交于点O'，由菱形的性质得BO=12BD＝15cm，D'O'=12BD'＝18cm，AC＝2AO，A'C'＝2A'O'，BD⊥AC，BD'⊥A'C'，在Rt△AOB中由勾股定理可求出AO=153cm，则AC＝2AO=303cm，在Rt△A'O'D'中由勾股定理可求出A'O'＝24cm，则A'C'＝2A'O'＝48cm，然后再求出AC﹣A'C'即可．
【解答】解：设AC与BD交于点O，A'C'于BD'交于点O'，如下图所示：

依题意得：四边形ABCD，四边形A'BC'D'均为菱形，且AB＝A'D'＝30cm，BD＝30cm，BD'＝36cm，
∴BO=12BD＝15cm，D'O'=12BD'＝18cm，AC＝2AO，A'C'＝2A'O'，BD⊥AC，BD'⊥A'C'，
在Rt△AOB中，AB＝30cm，BO＝15cm，
由勾股定理得：AO=AB2−BO2=153（cm），
∴AC＝2AO=303cm，
在Rt△A'O'D'中，A'D'＝30cm，D'O'＝18cm，
由勾股定理得：A'O'=A'D'2−D'O'2=24（cm），
∴A'C'＝2A'O'＝48cm，
∴AC﹣A'C'=(303−48)cm，
即要使BD的长达到36cm，那么AC的长需要缩短(303−48)cm．
故选：D．
【点评】此题主要考查了菱形的性质，勾股定理，熟练掌握菱形的性质，灵活利用勾股定理进行计算是解决问题的关键．
二．填空题（共5小题）
11．如图，在矩形ABCD中，AD＝5，DC＝7，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，DH＝3，连接CF．当△FCG的面积为5时，DG的长为 7−5 ．
【考点】矩形的性质；三角形的面积；菱形的性质．
【专题】矩形 菱形 正方形；推理能力．
【答案】7−5．
【分析】作FM⊥DC，M为垂足，连接GE，可以证明△AHE≌△MFG，则FM＝HA＝2，即无论菱形EFGH如何变化，点F到直线CD的距离始终为定值2．根据△FCG的面积就可以解出GC，DG的长．
【解答】解：作FM⊥DC，M为垂足，连接GE，
∵AB∥CD，
∴∠AEG＝∠MGE，
∵HE∥GF，
∴∠HEG＝∠FGE，
∴∠AEH＝∠MGF．
在△AHE和△MFG中，∠A＝∠M＝90°，HE＝FG，
∴△AHE≌△MFG．
∴FM＝HA＝2，即无论菱形EFGH如何变化，点F到直线CD的距离始终为定值2．
因此S△FCG=12×2GC=5，解得GC=5，
∴DG＝7−5．
故答案为：7−5．
【点评】本题考查了矩形的性质，解决本题的关键是了解无论菱形EFGH如何变化，点F到直线CD的距离始终为定值2，难度不大．
12．如图，正八边形ABCDEFGH的对角线AF，HD交于点M，则∠AMH的度数是 67.5 °．
【考点】多边形内角与外角．
【专题】多边形与平行四边形；推理能力．
【答案】67.5．
【分析】先求出∠AHG＝∠HAB＝135°，再根据正八边形的性质求出∠AHD和∠MAH，最后根据三角形的内角和即可求得．
【解答】解：∵八边形ABCDEFGH为正八边形，
∵∠AHG＝∠HAB＝180°﹣360°÷8＝135°，
∵正八边形ABCDEFGH的对角线AF，HD，
∴∠AHD=12∠AHG＝67.5°，
∠FAB＝90°，
∴∠MAH＝135°﹣90°＝45°，
∴∠AMH＝180°﹣45°﹣67.5°＝67.5°．
故答案为：67.5．
【点评】本题主要考查多边形内角和外角，解题的关键是熟练掌握正多边形的性质．
13．如图，在正方形ABCD中，点E为CD上靠近点D的三等分点，点F为BC的中点，以EF为直角边，点E为直角顶点向右构造等腰Rt△EFG，连接AG、CG，则AGCG的值为 58517 ．
【考点】正方形的性质；全等三角形的判定与性质；勾股定理；等腰直角三角形．
【专题】图形的全等；等腰三角形与直角三角形；矩形 菱形 正方形；几何直观；运算能力；推理能力．
【答案】58517．
【分析】过点G作GM⊥CD于M，GM的延长线交AB于N，根据点E为CD上靠近点D的三等分点，设DE＝2a，则EC＝4a，AB＝BC＝DC＝AD＝6a，BF＝CF＝3a，证明四边形ANMD和四边形BCMN均为矩形，则MN＝AD＝6a，BN＝CM，再证明△FEC和△EGM全等得CF＝EM＝3a，EC＝GM＝4a，则BN＝CM＝CE﹣EM＝a，GN＝GM+MN＝10a，AN＝AB﹣BN＝5a，然后由勾股定理分别求出AG=55a，CG=17a，据此可得AGCG的值．
【解答】解：过点G作GM⊥CD于M，GM的延长线交AB于N，如下图所示：
∵点E为CD上靠近点D的三等分点，
∴设DE＝2a，则EC＝4a，
∴CD＝DE+EC＝6a，
∵四边形ABCD为正方形，
∴AB＝BC＝DC＝AD＝6a，∠ABC＝∠BCD＝∠D＝∠DAB＝90°，
∵点F在BC的中点，
∴BF＝CF＝3a，
∵GM⊥CD于M，GM的延长线交AB于N，
∴四边形ANMD和四边形BCMN均为矩形，
∴MN＝AD＝6a，BN＝CM，
∵△EFG为等腰直角三角形，且点E为直角顶点，
∴EF＝EG，∠FEG＝90°，
∴∠FEC+∠MEG＝90°，
∵∠BCD＝90°，GM⊥CD，
∴∠FCE＝∠EMG＝90°，
∴∠MEG+∠EGM＝90°，
∴∠FEC＝∠EGM，
在△FEC和△EGM中，
∠FCE=∠EMG=90°∠FEC=∠EGMEF=EG，
∴△FEC≌△EGM（AAS），
∴CF＝EM＝3a，EC＝GM＝4a，
∴BN＝CM＝CE﹣EM＝4a﹣3a＝a，GN＝GM+MN＝4a+6a＝10a，
∴AN＝AB﹣BN＝6a﹣a＝5a，
在Rt△AGN中，由勾股定理得：AG=AN2+GN2=55a，
在Rt△GCM中，由勾股定理得：CG=GM2+CM2=17a，
∴AGCG=55a17a=58517．
【点评】此题主要考查了正方形的性质，等腰直角三角形的性质，全等三角形的判定和性质，勾股定理等，理解正方形的性质，等腰直角三角形的性质，熟练掌握全等三角形的判定和性质，灵活运用勾股定理进行计算是解决问题的关键．
14．如图，在矩形ABCD中，AB＝6，AD＝12，E是线段AD上一动点，以E为直角顶点在EB的右侧作等腰三角形EBF，连接DF，当点F落在矩形ABCD的对角线上时，则DF的长为 25 或6 ．
【考点】矩形的性质；解直角三角形；全等三角形的判定与性质；等腰三角形的性质．
【专题】函数及其图象；等腰三角形与直角三角形；矩形 菱形 正方形；解直角三角形及其应用；推理能力．
【答案】25或6．
【分析】由“AAS”可证△ABE≌△HEF，可得AB＝EH＝6，AE＝HF，分两种情况讨论，由锐角三角函数可求解．
【解答】解：如图，过点F作FH⊥AD于H，
∴∠FHE＝∠BEF＝90°＝∠BAE，
∴∠ABE+∠AEB＝90°＝∠AEB+∠FEH，
∴∠ABE＝∠FEH，
又∵BE＝EF，
∴△ABE≌△HEF（AAS），
∴AB＝EH＝6，AE＝HF，
设AE＝HF＝x，
∴DH＝12﹣6﹣x＝6﹣x，
当点F在BD上时，tan∠ADB=ABAD=HFHD=12，
∴x6−x=12，
∴x＝2，
∴HF＝2，DH＝4，
∴DF=HD2+HF2=4+16=25，
当点F在AC上时，tan∠DAC=DCAD=HFAH=12，
∴x6+x=12，
∴x＝6，
∴HF＝6，DH＝0，
∴点F与点C重合，点H与点D重合，
∴DF＝6，
故答案为：25或6．
【点评】本题考查了矩形的性质，等腰直角三角形的性质，全等三角形的判定和性质，锐角三角函数等知识，添加恰当辅助线构造全等三角形是解题的关键．
15．如图是由6个形状、大小完全相同的菱形组成的网格，菱形的顶点称为格点，已知菱形的一个角（∠O）为60°，点A，B，C都在格点上，则sin∠ABC的值是 217 ．
【考点】菱形的性质；解直角三角形．
【专题】矩形 菱形 正方形；运算能力．
【答案】见试题解答内容
【分析】如图，连接EA、EC，先证明∠AEC＝90°，E、C、B共线，再根据sin∠ABC=AEAB，求出AE、AB即可解决问题．
【解答】解：如图，连接EA，EC，
设菱形的边长为a，由题意得∠AEF＝30°，∠CEF＝60°，
∴AE＝2cs30°•a=3a，EC＝a，
则AC＝2a，
∴AE2+CE2＝AC2，
∴∠AEC＝90°，
∴∠ACE＝60°，
∴∠ACE＝∠ACG＝∠BCG＝60°，
∴∠ECB＝180°，
∴E、C、B共线，
在Rt△AEB中，sin∠ABC=AEAB=3a7a=217．
故答案为：217．
【点评】本题考查菱形的性质，三角函数、特殊三角形边角关系等知识，解题的关键是添加辅助线构造直角三角形解决问题，属于中考常考题型．
三．解答题（共5小题）
16．如图，在矩形ABCD中，E为AB边上一点，EC平分∠DEB，F为CE的中点，连接AF，BF，过点E作EH∥BC分别交AF，CD于G，H两点．
（1）求证：AB＝DE；
（2）请判断AF，BF的位置关系，并说明理由．
【考点】矩形的性质；全等三角形的判定与性质．
【专题】图形的全等；矩形 菱形 正方形；推理能力．
【答案】（1）证明见解析；
（2）AF⊥BF，理由见解析．
【分析】（1）由矩形的性质得出AB∥CD，AB＝CD，根据平行线的性质得出∠DCE＝∠BEC，根据角平分线的定义得出∠DEC＝∠BEC，于是有∠DCE＝∠DEC，根据等角对等边得到CD＝DE，于是问题得证；
（2）连接DF，先证△DCF和△ABF全等，再证∠DFC＝90°，即可得出AF，BF的位置关系．
【解答】（1）证明：∵四边形ABCD是矩形，
∴AB∥CD，AB＝CD，
∴∠DCE＝∠BEC，
∵EC平分∠DEB，
∴∠DEC＝∠BEC，
∴∠DCE＝∠DEC，
∴CD＝DE，
∴AB＝DE；
（2）解：AF⊥BF，理由：
如图，连接DF，
∵四边形ABCD是矩形，
∴AB∥CD，AB＝CD，∠ABC＝∠BCD＝90°，
∵F为CE的中点，
∴BF=12CE=CF＝EF，
∴∠FBA＝∠BEC，
∵AB∥CD，
∴∠DCE＝∠BEC，
∴∠DCF＝∠FBA，
在△DCF和△ABF中，
CD=BA∠DCF=∠ABFCF=BF，
∴△DCF≌△ABF（SAS），
∴∠DFC＝∠AFB，
由（1）知CD＝DE，F为CE的中点，
∴DF⊥CE，
∴∠DFC＝90°，
∴∠AFB＝90°，
即AF⊥BF．
【点评】本题考查了矩形的性质，全等三角形的判定与性质，等腰三角形的判定与性质，平行线的性质，角平分线的定义，熟练掌握这些知识点是解题的关键．
17．如图，BD平分∠ABF，点A是射线BM上一点，过点A作AD∥BN交BG于点D，过A作AE⊥BN，过点D作DF⊥BN．
（1）求证：四边形AEFD是矩形；
（2）在BF上取点C使得CF＝BE，连接AC、CD．求证：AC⊥BD．
【考点】矩形的判定与性质．
【专题】矩形 菱形 正方形；几何直观；推理能力．
【答案】（1）证明见解析过程；
（2）证明见解析过程．
【分析】（1）先判定四边形AEFD是平行四边形，然后由AE⊥BN即可得解；
（2）先判定四边形ABCD是平行四边形，再由BD平分∠ABC和AD∥BC得出AD＝AB，证出四边形ABCD是菱形，进而即可得证．
【解答】证明：（1）∵AE⊥BN，DF⊥BN，
∴AE∥DF，
∵AD∥EF，
∴四边形AEFD是平行四边形，
∵AE⊥BN，
∴四边形AEFD是矩形；
（2）∵四边形AEFD是矩形，
∴AD∥EF，AD＝EF，
∵BE＝CF，
∴BC＝EF，
∴AD∥BC，AD＝BC，
∴四边形ABCD是平行四边形，
∵BD平分∠ABC，
∴∠ABD＝∠DBC，
∵AD∥BC，
∴∠ADB＝∠DBC，
∴∠ABD＝∠ADB，
∴AD＝AB，
∴四边形ABCD是菱形，
∴AC⊥BD．
【点评】本题主要考查了特殊四边形的判定和性质，角平线的性质等知识点，熟练掌握其判定和性质是解决此题的关键．
18．如图，在▱ABCD中，AE⊥BC于点E，延长BC至点F，使CF＝BE，连接DF，AF与DE交于点O．
（1）求证：四边形AEFD为矩形；
（2）若AB＝3，OE＝2，BF＝5，求DF的长．
【考点】矩形的判定与性质；平行四边形的性质．
【专题】矩形 菱形 正方形；推理能力．
【答案】（1）证明见解析；
（2）125．
【分析】（1）先证四边形AEFD为平行四边形，再证∠AEF＝90°，即可得出结论；
（2）由矩形的性质得DF＝AE，AF＝DE＝4，再由勾股定理的逆定理得△BAF为直角三角形，∠BAF＝90°，然后由面积法求出AE的长，即可得出答案．
【解答】（1）证明：∵BE＝CF，
∴BE+CE＝CF+CE，
即BC＝EF，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴AD＝BC＝EF，
又∵AD∥EF，
∴四边形AEFD为平行四边形，
∵AE⊥BC，
∴∠AEF＝90°，
∴平行四边形AEFD为矩形；
（2）解：由（1）知，四边形AEFD为矩形，
∴DF＝AE，AF＝DE＝2OE＝4，
∵AB＝3，DE＝4，BF＝5，
∴AB2+AF2＝BF2，
∴△BAF为直角三角形，∠BAF＝90°，
∴S△ABF=12AB×AF=12BF×AE，
∴AB×AF＝BF×AE，
即3×4＝5AE，
∴AE=125，
∴DF＝AE=125．
【点评】本题考查了矩形的判定与性质、平行四边形的判定与性质、勾股定理的逆定理以及三角形面积等知识，熟练掌握矩形的判定与性质是解题的关键．
19．如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB，交AB的延长线于点E，连接OE．
（1）求证：四边形ABCD是菱形．
（2）若AB＝5，BD＝6，求OE的长．
【考点】菱形的判定与性质；全等三角形的判定与性质；角平分线的性质；等腰三角形的判定与性质．
【专题】矩形 菱形 正方形；推理能力．
【答案】（1）见解析；
（2）4．
【分析】（1）根据题意先证明四边形ABCD是平行四边形，再由AB＝AD可得平行四边形ABCD是菱形；
（2）根据菱形的性质得出OB的长以及∠AOB＝90°，利用勾股定理求出OA的长，再根据直角三角形斜边中线定理得出OE＝AC，即可解答．
【解答】（1）证明：∵AB∥CD，
∴∠CAB＝∠DCA，
∵AC为∠DAB的平分线，
∴∠CAB＝∠DAC，
∴∠DCA＝∠DAC，
∴CD＝AD，
∵AB＝AD，
∴AB＝CD，
∵AB∥CD，
∴四边形ABCD是平行四边形，
∵AD＝AB，
∴平行四边形ABCD是菱形；
（2）解：∵四边形ABCD是菱形，对角线AC，BD交于点O，
∴AC⊥BD，OA＝OC=12AC，OB＝OD=12BD，
∴OB=12BD=3，
在Rt△AOB中，∠AOB＝90°，
∴OA=AB2−OB2=52−32=4，
∵CE⊥AB，
∴∠AEC＝90°，
在Rt△AEC中，∠AEC＝90°，O为AC中点，
∴OE=12AC=OA=4．
【点评】本题主要考查了菱形的判定和性质、勾股定理、直角三角形斜边的中线等于斜边的一半等知识，熟练掌握菱形的判定与性质是解题的关键．
20．如图，在矩形ABCD中，点F是BC上一点，且CF＝2BF，CE⊥AF，垂足为点E，∠BCE＝30°．
（1）求证：AE＝EF+CF；
（2）若AD＝6cm，点P是AD上一动点，以1cm/s的速度从点A运动到点D，问：点P运动多少秒四边形AFCP是菱形？请说明理由．
【考点】矩形的性质；全等三角形的判定与性质；菱形的判定．
【专题】矩形 菱形 正方形；运算能力．
【答案】（1）见解答过程；
（2）点P运动4秒，四边形AFCP是菱形．
【分析】（1）根据四边形ABCD是矩形，得出∠B＝90°，通过已知条件证明△ABF≌△CEF（ASA），再进行等量代换即可；
（2）设点P运动t秒，四边形AFCP是菱形，根据四边形AFCP是菱形，得出AP＝AF＝CF＝CP＝t，根据题意列出方程解答即可．
【解答】（1）证明：∵四边形ABCD是矩形，
∴∠B＝90°，
∵AF⊥CE，
∴∠E＝90°，
∵∠ECF＝30°，
∴EF=12CF，
∵CF＝2BF，
∴BF＝EF，
又∵∠AFB＝∠CFE，
∴△ABF≌△CEF（ASA），
∴AF＝CF，
∵AE＝EF+AF，
∴AE＝EF+CF；
（2）解：设点P运动t秒，四边形AFCP是菱形，
∵四边形AFCP是菱形，
∴AP＝AF＝CF＝CP＝t，
∵CF＝2BF，
∴BF=12t，
∵AD＝6，
∴BC＝6，
∴12t+t=6，
即：t＝4，
∴点P运动4秒，四边形AFCP是菱形．
【点评】本题主要考查了全等三角形的性质和判定，菱形的判定，矩形的性质，熟练掌握相关性质是解答本题的关键．
考点卡片
1．坐标与图形性质
1、点到坐标轴的距离与这个点的坐标是有区别的，表现在两个方面：①到x轴的距离与纵坐标有关，到y轴的距离与横坐标有关；②距离都是非负数，而坐标可以是负数，在由距离求坐标时，需要加上恰当的符号．
2、有图形中一些点的坐标求面积时，过已知点向坐标轴作垂线，然后求出相关的线段长，是解决这类问题的基本方法和规律．
3、若坐标系内的四边形是非规则四边形，通常用平行于坐标轴的辅助线用“割、补”法去解决问题．
2．反比例函数图象上点的坐标特征
反比例函数y＝k/x（k为常数，k≠0）的图象是双曲线，
①图象上的点（x，y）的横纵坐标的积是定值k，即xy＝k；
②双曲线是关于原点对称的，两个分支上的点也是关于原点对称；
③在y＝k/x图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
3．三角形的面积
（1）三角形的面积等于底边长与高线乘积的一半，即S△=12×底×高．
（2）三角形的中线将三角形分成面积相等的两部分．
4．三角形的稳定性
当三角形三边的长度确定后，三角形的形状和大小就能唯一确定下来，故三角形具有稳定性．这一特性主要应用在实际生活中．
5．全等三角形的判定与性质
（1）全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
（2）在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．
6．角平分线的性质
角平分线的性质：角的平分线上的点到角的两边的距离相等．
注意：①这里的距离是指点到角的两边垂线段的长；②该性质可以独立作为证明两条线段相等的依据，有时不必证明全等；③使用该结论的前提条件是图中有角平分线，有垂直角平分线的性质语言：如图，∵C在∠AOB的平分线上，CD⊥OA，CE⊥OB∴CD＝CE
7．线段垂直平分线的性质
（1）定义：经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线（中垂线）垂直平分线，简称“中垂线”．
（2）性质：①垂直平分线垂直且平分其所在线段． ②垂直平分线上任意一点，到线段两端点的距离相等． ③三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的距离相等．
8．等腰三角形的性质
（1）等腰三角形的概念
有两条边相等的三角形叫做等腰三角形．
（2）等腰三角形的性质
①等腰三角形的两腰相等
②等腰三角形的两个底角相等．【简称：等边对等角】
③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．【三线合一】
（3）在①等腰；②底边上的高；③底边上的中线；④顶角平分线．以上四个元素中，从中任意取出两个元素当成条件，就可以得到另外两个元素为结论．
9．等腰三角形的判定与性质
1、等腰三角形提供了好多相等的线段和相等的角，判定三角形是等腰三角形是证明线段相等、角相等的重要手段．
2、在等腰三角形有关问题中，会遇到一些添加辅助线的问题，其顶角平分线、底边上的高、底边上的中线是常见的辅助线，虽然“三线合一”，但添加辅助线时，有时作哪条线都可以，有时不同的做法引起解决问题的复杂程度不同，需要具体问题具体分析．
3、等腰三角形性质问题都可以利用三角形全等来解决，但要注意纠正不顾条件，一概依赖全等三角形的思维定势，凡可以直接利用等腰三角形的问题，应当优先选择简便方法来解决．
10．勾股定理
（1）勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2＝c2．
（2）勾股定理应用的前提条件是在直角三角形中．
（3）勾股定理公式a2+b2＝c2 的变形有：a=c2−b2，b=c2−a2及c=a2+b2．
（4）由于a2+b2＝c2＞a2，所以c＞a，同理c＞b，即直角三角形的斜边大于该直角三角形中的每一条直角边．
11．等腰直角三角形
（1）两条直角边相等的直角三角形叫做等腰直角三角形．
（2）等腰直角三角形是一种特殊的三角形，具有所有三角形的性质，还具备等腰三角形和直角三角形的所有性质．即：两个锐角都是45°，斜边上中线、角平分线、斜边上的高，三线合一，等腰直角三角形斜边上的高为外接圆的半径R，而高又为内切圆的直径（因为等腰直角三角形的两个小角均为45°，高又垂直于斜边，所以两个小三角形均为等腰直角三角形，则两腰相等）；
（3）若设等腰直角三角形内切圆的半径r＝1，则外接圆的半径R=2+1，所以r：R＝1：2+1．
12．三角形中位线定理
（1）三角形中位线定理：
三角形的中位线平行于第三边，并且等于第三边的一半．
（2）几何语言：
如图，∵点D、E分别是AB、AC的中点
∴DE∥BC，DE=12BC．
13．多边形
（1）多边形的概念：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形．
（2）多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线．
（3）正多边形的概念：各个角都相等，各条边都相等的多边形叫做正多边形．
（4）多边形可分为凸多边形和凹多边形，辨别凸多边形可用两种方法：①画多边形任何一边所在的直线整个多边形都在此直线的同一侧．②每个内角的度数均小于180°，通常所说的多边形指凸多边形．
（5）重心的定义：平面图形中，多边形的重心是当支撑或悬挂时图形能在水平面处于平稳状态，此时的支撑点或者悬挂点叫做平衡点，或重心．
常见图形的重心（1）线段：中点（2）平行四边形：对角线的交点（3）三角形：三边中线的交点（4）任意多边形．
14．多边形内角与外角
（1）多边形内角和定理：（n﹣2）•180° （n≥3且n为整数）
此公式推导的基本方法是从n边形的一个顶点出发引出（n﹣3）条对角线，将n边形分割为（n﹣2）个三角形，这（n﹣2）个三角形的所有内角之和正好是n边形的内角和．除此方法之和还有其他几种方法，但这些方法的基本思想是一样的．即将多边形转化为三角形，这也是研究多边形问题常用的方法．
（2）多边形的外角和等于360°．
①多边形的外角和指每个顶点处取一个外角，则n边形取n个外角，无论边数是几，其外角和永远为360°．
②借助内角和和邻补角概念共同推出以下结论：外角和＝180°n﹣（n﹣2）•180°＝360°．
15．平面镶嵌（密铺）
（1）平面图形镶嵌的定义：用形状，大小完全相同的一种或几种平面图形进行拼接．彼此之间不留空隙，不重叠地铺成一片，这就是平面图形的镶嵌．
（2）正多边形镶嵌有三个条件限制：①边长相等；②顶点公共；③在一个顶点处各正多边形的内角之和为360°．
判断一种或几种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角，若能构成360°，则说明能够进行平面镶嵌，反之则不能．
（3）单一正多边形的镶嵌：正三角形，正四边形，正六边形．
（4）两种正多边形的镶嵌：3个正三角形和2个正方形、四个正三角形和1个正六边形、2个正三角形和2个正六边形、1个正三角形和2个正十二边形、1个正方形和2个正八边形等．
（5）用任意的同一种三角形或四边形能镶嵌成一个平面图案．
16．平行四边形的性质
（1）平行四边形的概念：有两组对边分别平行的四边形叫做平行四边形．
（2）平行四边形的性质：
①边：平行四边形的对边相等．
②角：平行四边形的对角相等．
③对角线：平行四边形的对角线互相平分．
（3）平行线间的距离处处相等．
（4）平行四边形的面积：
①平行四边形的面积等于它的底和这个底上的高的积．
②同底（等底）同高（等高）的平行四边形面积相等．
17．平行四边形的判定
（1）两组对边分别平行的四边形是平行四边形．符号语言：∵AB∥DC，AD∥BC∴四边行ABCD是平行四边形．
（2）两组对边分别相等的四边形是平行四边形．符号语言：∵AB＝DC，AD＝BC∴四边行ABCD是平行四边形．
（3）一组对边平行且相等的四边形是平行四边形．
符号语言：∵AB∥DC，AB＝DC∴四边行ABCD是平行四边形．
（4）两组对角分别相等的四边形是平行四边形．
符号语言：∵∠ABC＝∠ADC，∠DAB＝∠DCB∴四边行ABCD是平行四边形．
（5）对角线互相平分的四边形是平行四边形．符号语言：∵OA＝OC，OB＝OD∴四边行ABCD是平行四边形．
18．菱形的性质
（1）菱形的性质
①菱形具有平行四边形的一切性质；
②菱形的四条边都相等；
③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；
④菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．
（2）菱形的面积计算
①利用平行四边形的面积公式．
②菱形面积=12ab．（a、b是两条对角线的长度）
19．菱形的判定
①菱形定义：一组邻边相等的平行四边形是菱形（平行四边形+一组邻边相等＝菱形）；
②四条边都相等的四边形是菱形．
几何语言：∵AB＝BC＝CD＝DA∴四边形ABCD是菱形；
③对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）．
几何语言：∵AC⊥BD，四边形ABCD是平行四边形∴平行四边形ABCD是菱形
20．菱形的判定与性质
（1）依次连接四边形各边中点所得的四边形称为中点四边形．不管原四边形的形状怎样改变，中点四边形的形状始终是平行四边形．
（2）菱形的中点四边形是矩形（对角线互相垂直的四边形的中点四边形定为矩形，对角线相等的四边形的中点四边形定为菱形．） （3）菱形是在平行四边形的前提下定义的，首先它是平行四边形，但它是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而就增加了一些特殊的性质和不同于平行四边形的判定方法．
（4）正方形是特殊的菱形，菱形不一定是正方形，所以，在同一平面上四边相等的图形不只是正方形．
21．矩形的性质
（1）矩形的定义：有一个角是直角的平行四边形是矩形．
（2）矩形的性质
①平行四边形的性质矩形都具有；
②角：矩形的四个角都是直角；
③边：邻边垂直；
④对角线：矩形的对角线相等；
⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．
（3）由矩形的性质，可以得到直角三角形的一个重要性质，直角三角形斜边上的中线等于斜边的一半．
22．矩形的判定与性质
（1）关于矩形，应从平行四边形的内角的变化上认识其特殊性：一个内角是直角的平行四边形，进一步研究其特有的性质：是轴对称图形、内角都是直角、对角线相等．同时平行四边形的性质矩形也都具有．
在处理许多几何问题中，若能灵活运用矩形的这些性质，则可以简捷地解决与角、线段等有关的问题．
（2）下面的结论对于证题也是有用的：①△OAB、△OBC都是等腰三角形；②∠OAB＝∠OBA，∠OCB＝∠OBC；③点O到三个顶点的距离都相等．
23．正方形的性质
（1）正方形的定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．
（2）正方形的性质
①正方形的四条边都相等，四个角都是直角；
②正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；
③正方形具有四边形、平行四边形、矩形、菱形的一切性质．
④两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．
24．相似三角形的判定与性质
（1）相似三角形是相似多边形的特殊情形，它沿袭相似多边形的定义，从对应边的比相等和对应角相等两方面下定义；反过来，两个三角形相似也有对应角相等，对应边的比相等．
（2）三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；或依据基本图形对图形进行分解、组合；或作辅助线构造相似三角形，判定三角形相似的方法有时可单独使用，有时需要综合运用，无论是单独使用还是综合运用，都要具备应有的条件方可．
25．解直角三角形
（1）解直角三角形的定义
在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
（2）解直角三角形要用到的关系
①锐角、直角之间的关系：∠A+∠B＝90°；
②三边之间的关系：a2+b2＝c2；
③边角之间的关系：
sinA=∠A的对边斜边=ac，csA=∠A的邻边斜边=bc，tanA=∠A的对边∠A的邻边=ab．
（a，b，c分别是∠A、∠B、∠C的对边）