

2024-2025学年湖南省娄底市涟源市高一上册12月联考数学检测试卷(含解析)
展开
这是一份2024-2025学年湖南省娄底市涟源市高一上册12月联考数学检测试卷(含解析),共12页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
第Ⅰ卷(选择题)
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合,,则( )
A. B.
C. D.
答案:D
解析:,故.
故选:D
2. 函数的零点所在区间是( )
A. B. C. D.
答案:B
解析:在上单调递增,
,
所以的零点在区间.
故选:B
3. 若函数,则f(f(10)=
A. lg101B. 2C. 1D. 0
答案:B
解析:因为,所以.
所以,故选B.
4. 在单位圆中,已知角是第二象限角,它的终边与单位圆交于点,则( )
A. B. C. D.
答案:D
解析:由题意,,解得,
所以,
故选:D
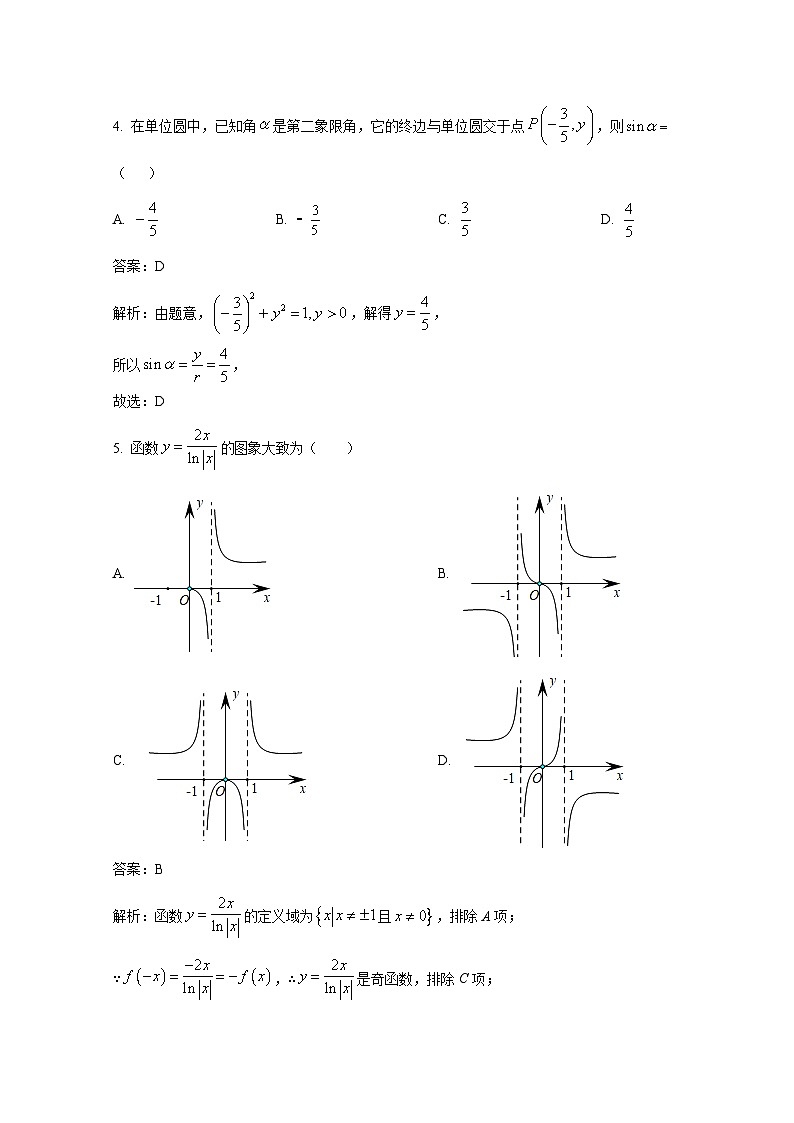
5. 函数图象大致为( )
A. B.
C. D.
答案:B
解析:函数的定义域为且,排除A项;
∵,∴是奇函数,排除C项;
再取特殊值当时,,排除D项.
故选:B.
6. 生物丰富度指数是河流水质的一个评价指标,其中,分别表示河流中的生物种类数与生物个体总数.生物丰富度指数越大,水质越好.如果某河流治理前后的生物种类数没有变化,生物个体总数由变为,生物丰富度指数由2提高到3,则( )
A. B. C. D.
答案:D
解析:由已知,,所以,即,∴,
故选:D.
7. 若两个正实数,满足,且不等式有解,则实数取值范围是( )
A. B. 或
C. D. 或
答案:D
解析:不等式有解,
,
,
,
当且仅当,等号成立,
,,,
实数的取值范围是.
故选:D.
8. 已知函数若函数有四个不同的零点,则实数的取值范围为( )
A. B. C. D.
答案:A
解析:
依题意,函数有四个不同的零点,即有四个解,
转化为函数与图象由四个交点,
由函数函数可知,
当时,函数单调递减函数,;
当时,函数为单调递增函数,;
当时,函数为单调递减函数,;
当时,函数为单调递增函数,;
结合图象,可知实数的取值范围为.
故选:A
二、多选题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.)
9. 下列说法正确的是( )
A. 小于的角是锐角
B. 与终边相同的角可表达为,
C. 钝角是第二象限角
D. 经过4小时,时针转了
答案:BCD
解析:对A,小于的角还包括和负角度的角,故A错误;
对B,,其终边与角相同,又,也为终边与角相同的角,故B正确;
对C,钝角是第二象限角,故C正确;
对D,时钟旋转为顺时针,故经过4小时,时针转了,故D正确.
故选:BCD
10. 下列说法正确的是( )
A. 命题“”的否定是“”
B. 是的必要不充分条件
C. 的单调减区间为
D. 函数且的图象恒过定点.
答案:ABD
解析:对于A,易知命题“”的否定是“”,故A正确;
对于B,不能推出,充分性不成立,能推出,必要性成立,
故是的必要不充分条件,故B正确;
对于C,fx=1x的单调减区间为,不能用并集符号,故C错误;
对于D,由且可令,解得,
又,故函数的图象恒过定点,故D正确.
故选:ABD
11. 已知,,则下列说法正确的是( )
A. 若,则
B. 若,则
C. 若,则
D. 若,则
答案:ACD
解析:因为,,
对于A,,当且仅当时取等号,故A选项正确;
对于B,,
故,当且仅当时取等号,故B选项错误;
对于C,∵,∴,∴在R上单调递增,
∵,∴,即,故C选项正确;
对于D,由得,
,
当且仅当,即时,等号成立,故D选项正确.
故选:ACD.
第Ⅱ卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知的圆心角所对的弧长为,则这个扇形的面积为_____.
答案:
解析:由题意,,故这个扇形的半径,面积为.
故答案:
13. 已知函数为,在R上单调递增,则取值范围_______.
答案:
解析:因为fx在上单调递增,且时,单调递增,
则需满足,解得,
则取值的范围为.
故答案为.
14. 若关于的不等式对任意恒成立,则实数的取值范围为_____.
答案:
解析:时,,设,则,
,
∴时,
所以,
故.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 化简求值:
(1)
(2).
答案:(1)4 (2)8
(1)解析:
原式.
(2)解析:
原式
.
16. 已知定义域为的函数满足对任意,都有.
(1)求证:是偶函数;
(2)设时,
①求证:在上是减函数;
②求不等式的解集.
答案:(1)证明见解析
(2)①证明见解析;②或或x>1
(1)解析:
取得,即,
取得,即,
取,得,即是偶函数;
(2)解析:
①设,则,
由时,得,
则,
即在上为减函数,
②由是偶函数且在上是减函数,
则不等式等价为,
即得,
得得,
即或或,
即不等式的解集为或或x>1..
17. 已知幂函数在上单调递减.
(1)求的解析式;
(2)若正数满足,求的最小值.
答案:(1)
(2)24
(1)解析:
幂函数在0,+∞上单调递减.
,解得,
.
(2)解析:
,正数满足,
,
都是正数,
,
当且仅当时,即时取等号,
的最小值为24.
18. “大禹门前树,千年苔子茶.”11月21日18时许,中央广播电视总台综合频道推出系列纪录片《农耕探文明》,本期正好关注到《四川北川苔子茶复合栽培系统》.北川苔子茶的“毛峰绿茶”以其外形匀整、挺秀,汤色碧绿,香气浓烈等优异品质闻名遐迩,深受广大消费者青睐.经验表明,在室温下,该茶用的水泡制,汤色青绿明亮,入口滋味较薄有熟栗子香,无苦涩感,再等到茶水温度降至50°C时饮用,可以产生最佳饮用口感.经过研究发现,设茶水温度从开始,经过分钟后的温度为且满足.
(1)求常数的值;
(2)经过测试可知,求在室温下,刚泡好的该茶大约需要放置多长时间才能达到最佳饮用口感?(参考数据:,)
答案:(1)
(2)9.5分钟
(1)解析:
茶水温度从开始
当时,,
(2)解析:
当时,
当时,
刚泡好的茶水大约需要放置9.5分钟才能达到最佳饮用口感
19. 已知定义在上的函数是奇函数.
(1)求函数的解析式;
(2)解不等式;
(3)设函数,若,使得,求实数的取值范围.
答案:(1)
(2)或
(3)
(1)解析:
因为定义域是上的奇函数,
所以,即
解得.
经验证时,是奇函数.
(2)解析:
设,则,
因为在上递增,且在上递减,
所以是上减函数,
又因为在上是奇函数,
则可转化为,
且在是减函数,则,
整理得,解得或,
可得或,
所以不等式的解集为或.
(3)解析:
由题意可得
因为,即,则,可得,
所以的值域是,
若,使成立,只需,
设,则
可知在[1,2]上单调递增,
可知,
即时,取到最大值为,
所以,解得,
所以实数的取值范围.
相关试卷
这是一份湖南省娄底市涟源市部分学校2024-2025学年高一上学期选科考试暨12月联考数学试卷(含答案),共12页。试卷主要包含了选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
这是一份湖南省娄底市涟源市部分学校2024-2025学年高一上学期选科考试(12月联考)数学试题(Word版附解析),文件包含湖南省娄底市涟源市部分学校2024-2025学年高一上学期选科考试12月数学试题Word版含解析docx、湖南省娄底市涟源市部分学校2024-2025学年高一上学期选科考试12月数学试题Word版无答案docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
这是一份2023-2024学年湖南省娄底市涟源市高一(上)期末数学试卷,共4页。








