艺考生教学课件30简单几何体的表面积与体积-2024-2025学年高考数学艺体生一轮复习课件

这是一份艺考生教学课件30简单几何体的表面积与体积-2024-2025学年高考数学艺体生一轮复习课件，共60页。PPT课件主要包含了基本立体图形，空间几何体的表面积，空间几何体的体积，教材知识萃取，教材素材变式等内容，欢迎下载使用。
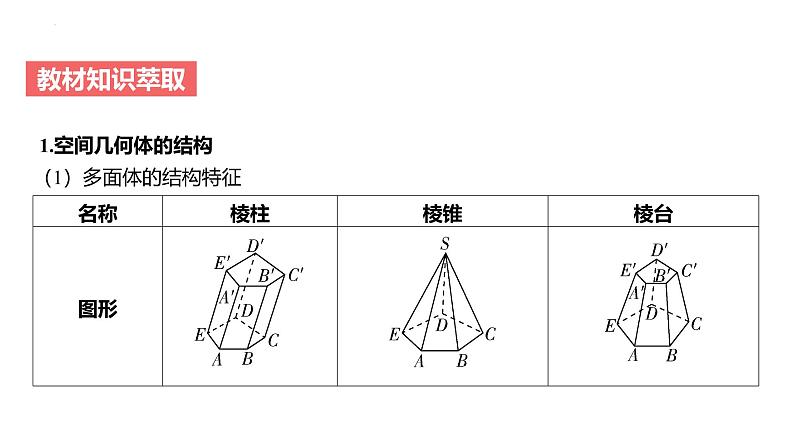
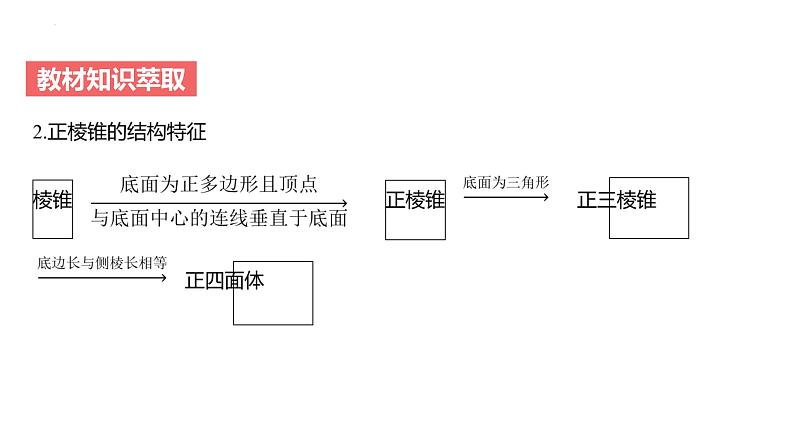
（1）多面体的结构特征
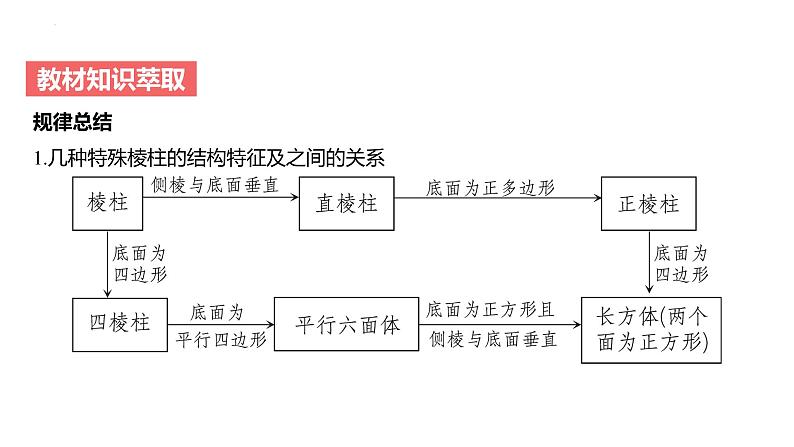
规律总结1.几种特殊棱柱的结构特征及之间的关系
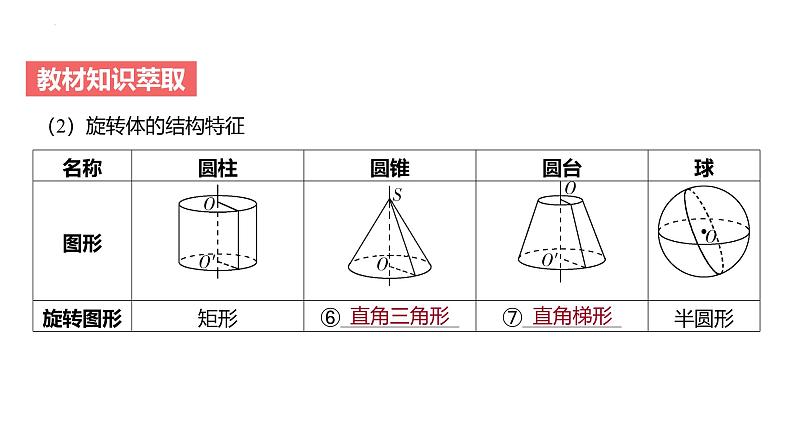
（2）旋转体的结构特征
等腰三角形
2.立体图形的直观图
（1）画法：常用斜二测画法.
1.正方体的基本截面用一个平面截正方体，可以得到的截面形状如下：
在这里需要给大家强调一下，正方体的斜截面不会出现以下几种图形：直角三角形、钝角三角形、直角梯形、正五边形.
2.圆柱体的基本截面用一个平面截圆柱，可以得到的截面形状如下：
方法技巧求解截面的面积（或面积的最值）问题，关键是准确判断截面的形状.
（1）如果截面的几何图形确定，那么可以利用平面几何知识求出其面积的大小；
（2）如果截面的几何图形不确定，那么可以讨论截面几何图形面积的最大、最小值，此时求解需要根据题意设立相关点的位置参量，建立截面面积的目标函数，然后利用函数知识求解.注意 在求解截面面积的最值时，需要根据几何体和截面的变化来确定相关参量的取值范围.
1.作截面的三种常用方法一是直接法，解题关键是截面上的点在几何体的棱上，且两两在一个平面内，可以直接借助基本事实2作出截面.二是作平行线法，解题关键是截面与几何体的两个平行平面相交，或者截面上有一条直线与几何体的某一个面平行，可借助线面平行的性质定理和面面平行的性质定理作出截面.三是延长交线得交点，解题关键是截面上的点中至少有两个点在几何体的同一个面上，可通过由作延长线得到的交点辅助得出截面与立体几何图形的交点，进而得交线和截面图形.
2.求解截面的交线长度问题，关键是准确找到截面与几何体相交的轨迹形状，突破口是找到截面与几何体的公共点的位置和变化轨迹.常见的轨迹形状为特殊四边形（正方形、平行四边形、菱形、梯形）的组合图形、圆周或圆弧、圆锥曲线的部分等.
1.［人A必修二P105习题8.1第4题变式］下面四个几何体中，是棱台的是( )
A.&1& B.&2& C.&3& D.&4&
【解析】选项A中几何体是圆台，选项C中几何体的四条侧棱的延长线没有相交于一点，不是棱台，选项D中几何体是棱锥，易知选项B中几何体是棱台，故选B．
2.［多选］［苏教必修二P156例3变式］对如图所示的组合体的结构特征有以下几种说法，其中正确的是( )
A.由一个长方体割去一个四棱柱所构成B.由一个长方体与两个四棱柱组合而成C.由一个长方体挖去一个四棱台所构成D.由一个长方体与两个四棱台组合而成
4.［多选］［人A必修二P104练习第3题变式］下列说法正确的是( )
A.以直角梯形的一腰所在直线为旋转轴，其余各边旋转一周形成的面所围成的旋转体是圆台B.以等腰三角形的底边上的高线所在直线为旋转轴，其余各边旋转一周形成的面所围成的旋转体是圆锥C.用一个平面去截球，得到的截面是一个圆面D.圆锥的轴截面是所有过顶点的截面中，面积最大的一个
（1）圆柱、圆锥、圆台的侧面展开图及侧面积公式
（2）简单几何体的表面积
方法技巧求空间几何体的表面积的常见类型及解题思路
2.［人A必修二P116练习第1题变式］已知正四棱台的上底面边长为2，下底面边长为4，高为3，则其表面积为 ( )
3.［人A必修二P116练习第3题变式］鲁班锁起源于中国古代建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分（即榫卯结构）啮合，十分巧妙.鲁班锁类玩具比较多，形状和内部的构造各不相同，一般都是易拆难装，如图1，这是一种常见的鲁班锁类玩具，图2是该鲁班锁类玩具的直观图.已知该鲁班锁类玩具每条棱的长均为1，则该鲁班锁类玩具的表面积为( )
方法总结求几何体的表面积的方法（1）求几何体的表面积问题的基本思路是将立体几何问题转化为平面几何问题，即空间图形平面化；（2）求不规则几何体的表面积时，通常将所给几何体分割成基本的柱体、锥体、台体等，通过求和或作差得到不规则几何体的表面积．特别提醒：求组合体的表面积时，要注意衔接部分的处理，防止漏算或多算.
6.［人B必修四P82练习A第5题变式］已知一个圆锥的母线长为10，高为8，则该圆锥内切球的表面积与圆锥的表面积的比值为( )
方法技巧求空间几何体体积的常用方法
方法技巧求解体积的最值问题的方法
（1）几何法：根据几何体的结构特征，先确定体积表达式中的常量与变量，然后利用几何知识判断变量什么情况下取得最值，从而确定体积的最值.
（2）代数法：先设变量，求出几何体的体积表达式，然后转化为函数最值问题或利用不等式求解即可.
方法技巧解决外接球问题的关键是抓住外接球的特点，即球心到多面体的顶点的距离等于球的半径．求几何体外接球半径的思路如下：
（2）将几何体补形成长方体（或正方体），利用几何体与长方体（或正方体）共有外接球的特征，由外接球的直径等于长方体（或正方体）的体对角线长求解.如三条侧棱互相垂直的三棱锥，当侧棱长相等时可补形成正方体，当侧棱长不相等时可补形成长方体.
方法技巧求解常见几何体的内切球半径的方法