中考数学二轮复习几何专项知识精讲+基础提优训练专题24 正方形存在性问题（知识精讲）

这是一份中考数学二轮复习几何专项知识精讲+基础提优训练专题24 正方形存在性问题（知识精讲），共7页。试卷主要包含了关于正方形的基础知识，正方形存在性问题解决策略等内容，欢迎下载使用。
1.正方形的定义
四条边相等，四个角都是直角的四边形叫做正方形；
2.正方形的性质（正方形具有四边形、平行四边形、矩形、菱形的一切性质）
边：四边相等，邻边垂直，对边平行；
角：四个角都是直角；
对角线：对角线相等，对角线互相垂直平分，每条对角线平分一组对角；
正方形是轴对称图形，有4条对称轴；
正方形是中心对称图形，两条对角线的交点就是对称中心.
3.正方形的判定
四条边相等，四个角都是直角的四边形是正方形；
有一个角是直角，且有一组邻边相等的平行四边形是正方形；
有一组邻边相等的矩形是正方形；
有一个角是直角的菱形是正方形.
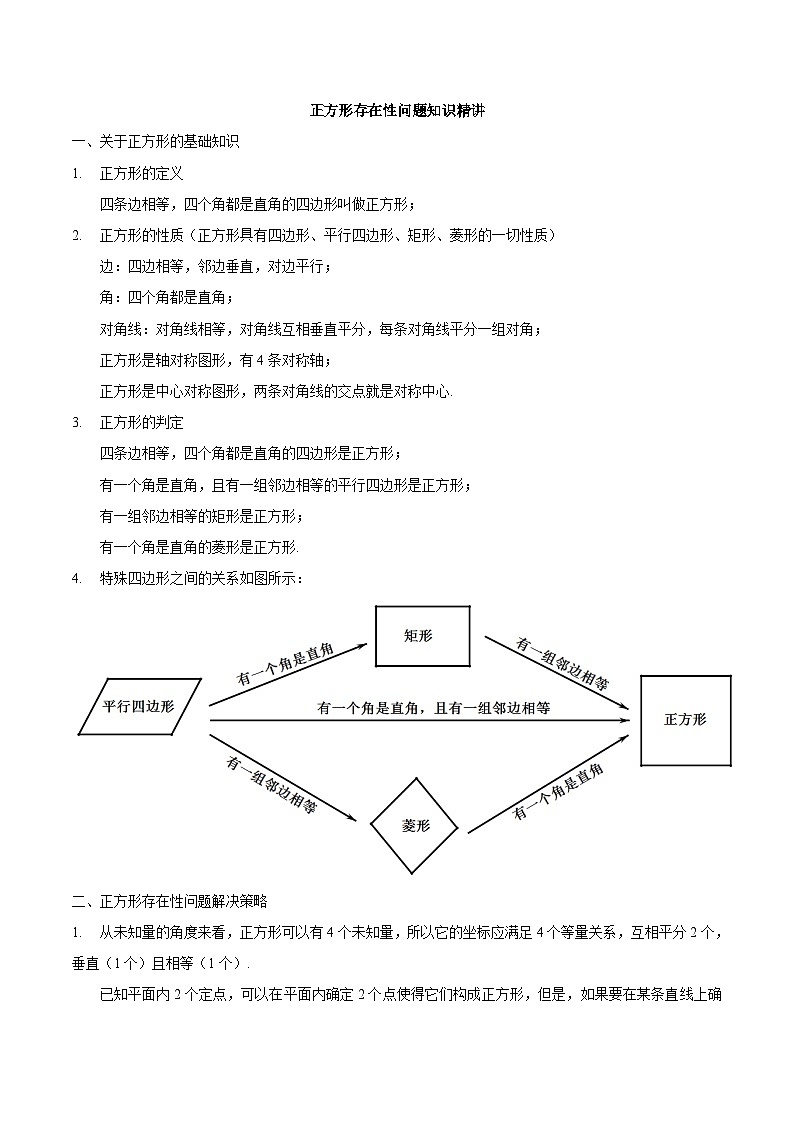
4.特殊四边形之间的关系如图所示：
二、正方形存在性问题解决策略
1.从未知量的角度来看，正方形可以有4个未知量，所以它的坐标应满足4个等量关系，互相平分2个，垂直（1个）且相等（1个）.
已知平面内2个定点，可以在平面内确定2个点使得它们构成正方形，但是，如果要在某条直线上确定点，很有可能会出现不存在的情况（未知量小于方程个数，无解）.
解决正方形存在性问题一般不用代数法，因为要列四元一次方程组，比较麻烦！
2.解决正方形存在性问题常用方法
①从正方形判定入手
若已知菱形，则证明一个角是直角或者对角线相等；
若已知矩形，则证明一组邻边相等或对角线互相垂直；
若已知对角线互相垂直或平分或相等，则加上其他条件即可.
②构造三垂直全等
若条件并未给出关于四边形对角线的特殊性，一般任取3个顶点必然是等腰直角三角形，如果已经知道了两个定点，则可以通过构造三垂直全等来求出第3个点，然后再进一步求出第4个点.
若题目中给了4个动点，则先要判断此时的四边形是否为特殊的四边形，在特殊四边形基础上，再添加某些条件，使得其构成一个正方形.
例1：如图，在矩形ABCD中，AB＝16cm，AD＝6cm，动点P，Q分别从点A，C同时出发，点P以每秒3cm的速度向点B移动，点Q以每秒2cm测得速度向点D移动，当点P到达点B处时，两点均停止移动，问：
（1）P，Q两点出发多长时间，线段PQ的长度为10cm？
（2）是否存在某一时刻，使四边形PBCQ为正方形？若存在，求出该时刻；若不存在，请说明理由．
【解答】（1）P，Q两点出发或秒，线段PQ的长度为10cm；（2）不存在
【解析】（1）过点P作PH⊥CD于点H，如图所示：
∴HQ＝16﹣5t，
∴PQ2＝PH2+HQ2，
即102＝（16﹣5t）2+62，
解得，
答：P，Q两点出发或秒，线段PQ的长度为10cm；
（2）∵四边形PBCQ是正方形，
∴BP＝CQ，即16﹣3t＝2t，
解得，
∵，
∴不成立．
例2：如图，已知抛物线交x轴于点A、点B，交y轴于点C，且点A（6，0），点C（0，4），AB＝5OB，设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形．
（1）求抛物线解析式及顶点坐标；
（2）求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；
（3）当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形？
（4）是否存在点E，使平行四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．
【解答】（1）y＝ax2+bx+c，顶点坐标为；（2）S=﹣4x2+28x﹣24（1＜x＜6）；（3）不是菱形；（4）不存在
【解析】（1）∵点A（6，0），AB＝5OB，
∴点B（1，0），
设所求抛物线的解析式为y＝ax2+bx+c，
则由题意可得：，解得，
∴所求抛物线的解析式为，
∵，
∴所求抛物线的顶点坐标为；
（2）∵点E（x，y）在抛物线上，位于第四象限，且坐标适合，∴y＜0，
即﹣y＞0，﹣y表示点E到OA的距离．
∵OA是平行四边形OEAF的对角线，
∴S＝2S△OAE＝2××OA•|y|＝﹣6y＝﹣6（x2﹣x+4）＝﹣4x2+28x﹣24，
自变量x的取值范围为：1＜x＜6；
（3）根据题意得：﹣4x2+28x﹣24＝24，
解之，得x1＝3，x2＝4，
∴所求的点E有两个，分别为E1（3，﹣4），E2（4，﹣4），
∵点E1（3，﹣4），
∴OE＝5，，
∴OE＝AE，
∴平行四边形OEAF是菱形，
∵点E2（4，﹣4），
∴OE＝，，
∴不满足OE＝AE，
∴平行四边形OEAF不是菱形；
（4）∵当OA⊥EF，且OA＝EF时，平行四边形OEAF是正方形，此时点E坐标只能（3，﹣3），而坐标为（3，﹣3）点不在抛物线上，
∴不存在这样的点E，使平行四边形OEAF为正方形．
例3：如图，直线y＝﹣3x+3与x轴、y轴分别交于点A、B，抛物线y＝a（x﹣2）2+k经过点A、B，并与X轴交于另一点C，其顶点为P．
（1）求a，k的值；
（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求Q点的坐标；
（3）点M为抛物线上任意一点，点N为对称轴上任意一点，是否存在点M，N使以A，C，M，N为顶点的四边形为正方形？若存在，请求出求此正方形的边长．若不存在，请说明理由．
【解答】（1）a，k的值分别为1，﹣1；（2）Q（2，2）；（3）存在，边长为.
【解析】（1）∵直线y＝﹣3x+3与x轴、y轴分别交于点A、B，
∴A（1，0），B（0，3）．
又∵抛物线y＝a（x﹣2）2+k经过点A（1，0），B（0，3），
∴，解得，
故a，k的值分别为1，﹣1；
（2）如图，
设Q点的坐标为（2，m），对称轴x＝2交x轴于点F，过点B作BE垂直于直线x＝2于点E．
在Rt△AQF中，AQ2＝AF2+QF2＝1+m2，
在Rt△BQE中，BQ2＝BE2+EQ2＝4+（3﹣m）2，
∵AQ＝BQ，
∴1+m2＝4+（3﹣m）2，
∴m＝2，
∴Q点的坐标为（2，2）；
（3）如图，
当点N在对称轴上时，NC与AC不垂直，所以AC应为正方形的对角线．
∵对称轴x＝2是AC的中垂线，
∴M点与顶点P（2，﹣1）重合，N点为点P关于x轴的对称点，其坐标为（2，1）．
此时，MF＝NF＝AF＝CF＝1，且AC⊥MN，
∴四边形AMCN为正方形．
在Rt△AFN中，，
即正方形的边长为．