2024-2025学年四川省自贡市高三上册10月月数学检测试题

这是一份2024-2025学年四川省自贡市高三上册10月月数学检测试题，共4页。试卷主要包含了 已知全集，集合，则， 已知，则“”是“”的， 若对任意的，且，则的最小值是， 下列命题为真命题的是， 已知函数，则等内容，欢迎下载使用。
1. 已知全集，集合，则（ ）
A. B.
C. D.
2. 已知，则“”是“”的（ ）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
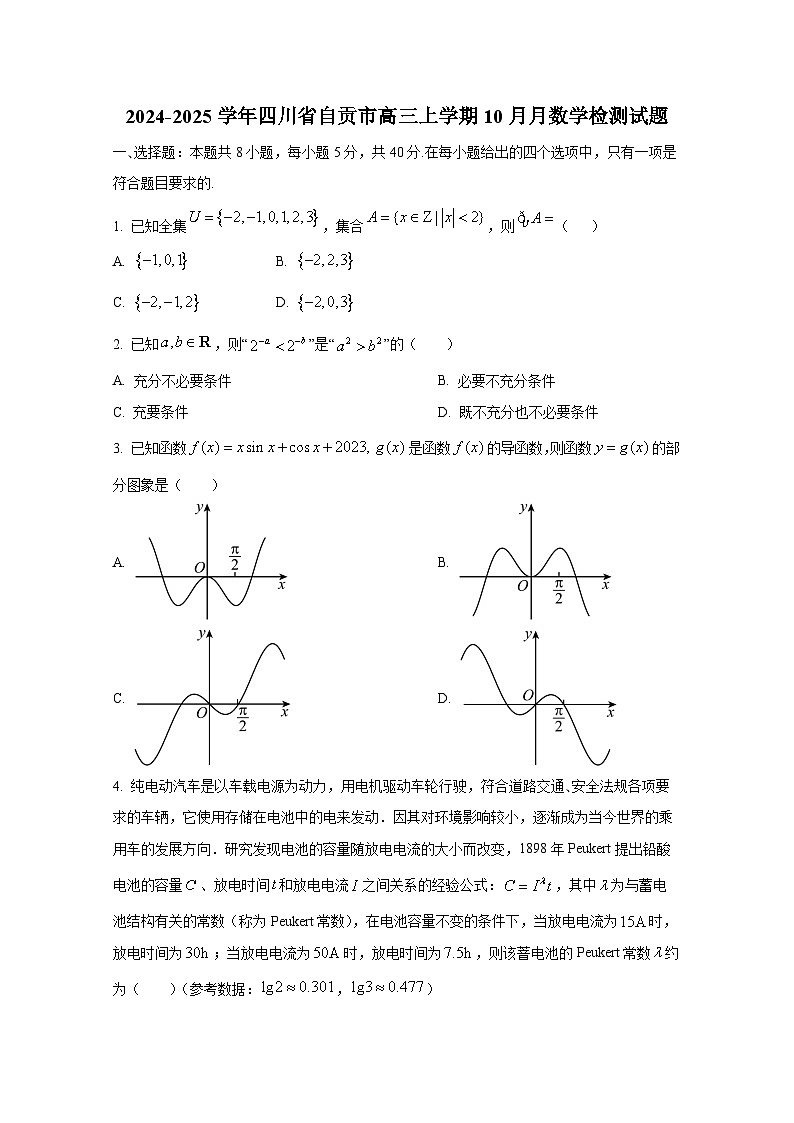
3. 已知函数是函数的导函数，则函数的部分图象是（ ）
A. B.
C. D.
4. 纯电动汽车是以车载电源为动力，用电机驱动车轮行驶，符合道路交通､安全法规各项要求的车辆，它使用存储在电池中的电来发动．因其对环境影响较小，逐渐成为当今世界的乘用车的发展方向．研究发现电池的容量随放电电流的大小而改变，1898年Peukert提出铅酸电池的容量、放电时间和放电电流之间关系的经验公式：，其中为与蓄电池结构有关的常数（称为Peukert常数），在电池容量不变的条件下，当放电电流为时，放电时间为；当放电电流为时，放电时间为，则该萻电池的Peukert常数约为（ ）（参考数据：，）
A. 1.12B. 1.13C. 1.14D. 1.15
5. 将函数的图象上所有点的横坐标缩短到原来的倍（纵坐标不变），再将所得图象向左平移个单位后得到的函数图象关于原点中心对称，则（ ）
A. B. C. D.
6. 若1为函数的极大值点，则实数a的取值范围是（ ）
A. B. C. D.
7. 已知奇函数在上是增函数，．若，，，则，，的大小关系为（ ）
A. B. C. D.
8. 若对任意的，且，则的最小值是（ ）
A. B. C. 1D.
二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项是符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9. 下列命题为真命题的是（ ）
A. “”是“”充分不必要条件
B. 命题“”的否定是“”
C. 若，则
D. 若，且，则的最小值为9
10. 已知函数，则（ ）
A. 的最小正周期为B. 是曲线的一个对称中心
C. 是曲线的一条对称轴D. 在区间上单调递增
11. 已知定义在R上函数满足，且是奇函数，则（ ）
A. 图象关于点对称
B.
C.
D. 若，则
三､填空题：本题共3小题，每小题5分，共15分.
12. 已知幂函数的图象关于轴对称，则实数的值是______．
13. 已知关于x的不等式恰有一个整数解，则实数a的取值范围是_________．
14. 我们知道，函数的图象关于坐标原点成中心对称图形的充要条件是函数为奇函数，有同学发现可以将其推广为：函数的图象关于点成中心对称图形的充要条件是函数为奇函数．
（1）请你利用这个结论求得函数的对称中心为_________．
（2）已知函数与一次函数有两个交点，，则_________．
四､解答题：本题共5小题，共77分（其中15题13分，16题和17各15分，18题和19题各17分）.解答应写出文字说明､证明过程或演算步骤.
15 已知函数．
（1）求曲线在点处的切线与坐标轴围成的三角形的面积；
（2）求的单调区间和极小值．
16. 已知数．
（1）求的最小正周期和对称轴方程；
（2）求在的最大值和最小值．
17. 已知函数，
（1）求函数的零点；
（2） 若函数有四个零点，求的取值范围；
（3）在（2）的条件下，记得四个零点从左到右分别为，，，，求值．
18. 在中，内角A，B，C的对边分别为a，b，c，且．
（1）求角B的大小；
（2）设，．
（ⅰ）求a的值；
（ⅱ）求的值．
19. 已知函数.
（1）讨论在区间上的单调性；
（2）若上有两个极值点.
①求实数的取值范围：
②求证.