福建省厦门双十中学2024-2025学年八年级上学期12月阶段考试数学试卷(含答案)

这是一份福建省厦门双十中学2024-2025学年八年级上学期12月阶段考试数学试卷(含答案)，共18页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．计算的结果为( )
A.B.0C.1D.3
2．下列运算正确的是( )
A.B.C.D.
3．下列分式与相等的是( )
A.B.C.D.
4．在平面直角坐标系中,点关于x轴的对称点的坐标为( )
A.B.C.D.
5．下列式子从左到右变形是因式分解的是( )
A.B.
C.D.
6．如图,点P在的内部,点C,D分别在,上,且,只添加一个条件即可证明和全等,这个条件不可以是( )
A.B.平分
C.平分D.
7．已知多项式可以运用平方差公式分解因式,则单项式M可以是( )
A.2abB.-2abC.3b2D.-5b2
8．如图,,AC和BC对应边分别是BE和DE,则下列与相等的是( )
A.B.C.D.
9．绿化队原来用漫灌方式浇绿地,a天用水m吨,现改用喷灌方式,可使这些水多用3天,则现在比原来每天节约用水吨数是( )
A.B.C.D.
10．如图为2024年某月日历,现用一个正方形方框框住部分(阴影部分)9个位置上的数,若最小的数与最大的数的积记为n,中间位置上的数记为m.下列所给的数据中,n不可能是( )
A.161B.298C.420D.465
二、填空题
11．计算：
(1)______；____________(2)______；
(3)______；______(4)______.
12．分式有意义,则x满足的条件是______.
13．分式与的最简公分母是______.
14．如果是完全平方式，则_________.
15．若,,则a与b的大小关系为______.
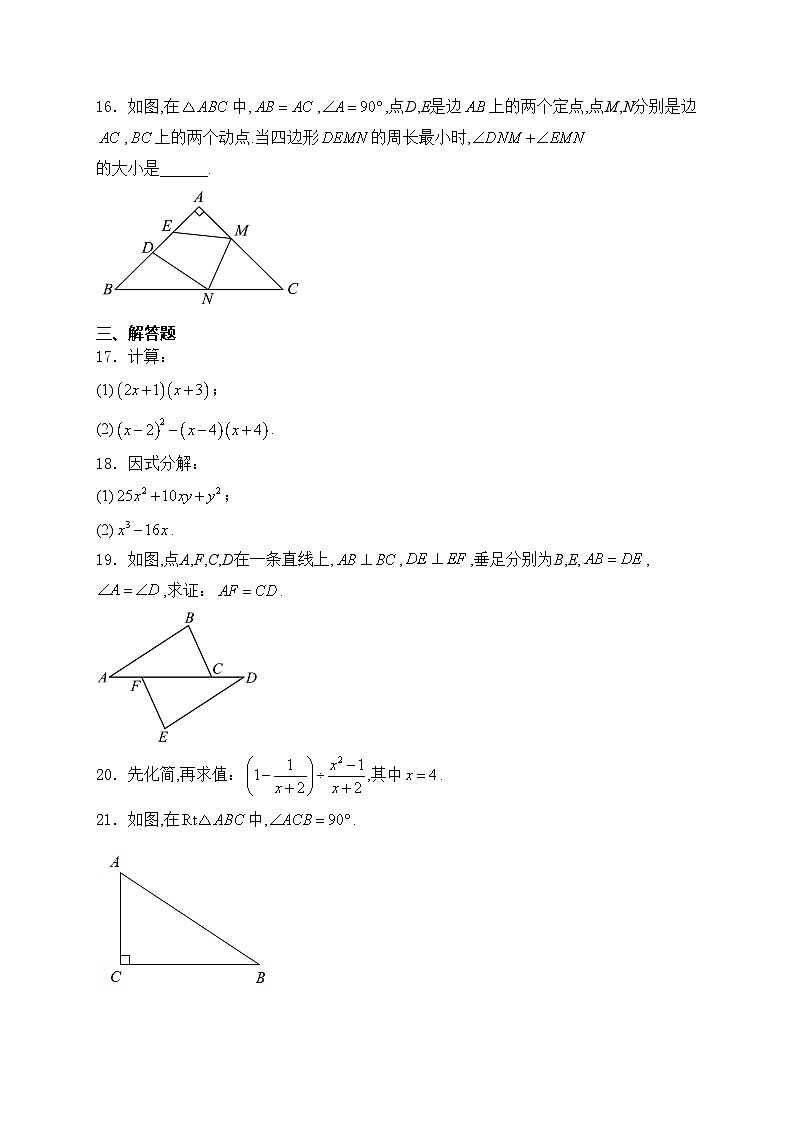
16．如图,在中,,,点D,E是边上的两个定点,点M,N分别是边,上的两个动点.当四边形的周长最小时,的大小是______.
三、解答题
17．计算：
(1)；
(2).
18．因式分解：
(1)；
(2).
19．如图,点A,F,C,D在一条直线上,,,垂足分别为B,E,,,求证：.
20．先化简,再求值：,其中.
21．如图,在中,.
(1)请用尺规作图法,在边上求作一点P,使得(保留作图痕迹,不要求写作法)；
(2)连接,若,证明为等边三角形.
22．“数形结合”是数学上一种重要的数学思想,在整式乘法中,我们常用图形而积来解释一些公式.如图(1),通过观察大长方形而积,可得：.
(1)如图(2),通过观察大正方形的面积,可以得到一个乘法公式,直接写出此公式；
(2)现有若干张如图(3)的三种纸片,A是边长为a的正方形,B是边长为b的正方形,C是长为a,宽为b的长方形.若要无缝无重叠拼出一个长为,宽为的长方形,设需要A型纸片x张,B型纸片y张,C型纸片z张,直接写出的值；
(3)图(4)是由图(3)中的两张A型纸片和两张B型纸片排成的一个正方形,其中两张A型纸片有重叠(图中阴影部分),直接写出阴影部分的面积(用含a,b的式子表示)；
(4)若图(2)也是由图(3)中的三种纸片拼成的,且图(2)中的阴影部分面积为17,图(4)中的阴影部分面积为8,求图(2)整个正方形的面积.
23．已知一些两位数相乘的算式：62×11,78×69,34×11,63×67,18×22,15×55,12×34,54×11.利用这些算式探究两位数乘法中可以简化运算的特殊情形：
(1)观察已知算式,选出具有共同特征的3个算式,并用文字描述它们的共同特征；
(2)分别计算你选出的算式.观察计算的结果,你能发现不经过乘法运算就可以快速、直接地写出积的规律吗？请用文字描述这个规律；
(3)证明你发现的规律；
(4)在已知算式中,找出所有可以应用(或经过转化可以应用)上述规律的算式,并将它们写在横线上：______.
24．通常把脏衣服用洗衣液清洗后会进行拧干,但由于不可能拧净衣服上的全部污水,所以还需要用清水进行多次漂洗,不断降低衣服中污水的含量.某小组研究了如何用清水漂洗衣服效果更好,部分内容如下,请补充完整：实验研究：先准备几件相同的洗过一次并拧干(存留一些污水)的衣服,把每件衣服分别用一定量的清水浸泡,经过充分搓洗,使清水与衣服上存留的污水混合均匀,然后拧干,视为一次漂洗,称重、记录每次漂洗后衣服上存留的污水重量和比例,如：把一件存留1斤污水的衣服用10斤清水漂洗后,拧干到仍然存留1斤污水,则漂洗后衣服中存有的污物是原来的,在多次实验后,通过对收集的数据进行分析,该小组决定使用20斤清水,采用三种不同的方案,对每件衣服分别进行漂洗,并假设每次拧干后的衣服上都存留约1斤的污水.
数据计算：对三种漂洗方案进行计算、比较.
方案一：采用一次漂洗的方式.将20斤清水一次用掉,漂洗后衣服中存有的污物是原来的______；
方案二：采用两次漂洗的方式,且两次用水量不同.如第一次用12斤清水,第二次用8斤清水,漂洗后衣服中存有的污物是原来的______；
方案三：采用两次漂洗的方式,且两次用水量相同,每次用10斤清水,漂洗后衣服中存有的污物是原来的______.
实验结论：对比可知,在这三种方案中,方案______的漂洗效果最好(填“一”“二”或“三”).
推广证明：将脏衣服用洗衣液清洗后,再用清水进行漂洗,假设每次拧干后还存留斤污水,现用斤清水漂洗(方案二中第一次用水量为x斤),证明上面实验中得到的结论.
25．如图,点,在平面直角坐标系中的坐标轴上,点为内一点,.
(1)求点P到的距离；
(2)如图1,射线交的垂直平分线于点C,试判断的形状,并说明理由；
(3)如图2,为x轴正半轴上一点,将沿所在直线翻折,与y轴,线段分别交于点F,G,试探究的周长是否会发生变化,若变化,求变化范围；若不变,求的周长.
参考答案
1．答案：C
解析：,
故选：C.
2．答案：C
解析：A.,选项运算错误；
B.,选项运算错误；
C.,选项运算正确；
D.,选项运算错误；
故选：C.
3．答案：D
解析：A.,故此选项不符合题意；
B.,故此选项不符合题意；
C.,故此选项不符合题意；
D.,故此选项符合题意；
故选：D.
4．答案：A
解析：关于x轴对称的点的坐标特征是横坐标相同,纵坐标互为相反数,从而点关于x轴对称的点的坐标是.故选A.
5．答案：D
解析：根据因式分解的定义,
选项A,右边不是积的形式,不是因式分解；
选项B,是整式的乘法,不是因式分解；
选项C,从左到右不是积的形式,不是因式分解；
选项D,左边等于右边是因式分解；
故选：D.
6．答案：C
解析：A、,可根据判定,故A不符合题意；
B、平分,可根据判定,故B不符合题意
C、平分,不能判定,故C不符合题意；
D、,可根据判定,故D不符合题意.
故选：C.
7．答案：D
解析：多项式可以运用平方差公式分解因式,
则单项式M可以是-5b2.
故选：D.
8．答案：B
解析：∵,
∴,,
∴,
∴,
∴.
故选：B.
9．答案：A
解析：原来每天的用水量为：,
现在每天的用水量为：,
∴现在比原来每天节约用水吨数是：,
故选：A.
10．答案：B
解析：最大和最小的两个数是和,
,
即,
A选项中,当时,,则,,,所以n可能是161,故A不符合题意；
B选项中,当时,,则没有正整数的平方等于,不符合日历,所以n不可能是298,故B符合题意；
C选项中,当时,,则,,,所以n可能是420,故C不符合题意；
D选项中,当时,,则,,,所以n可能是465,故D不符合题意；
故选：B.
11．答案：(1)
(2)
(3)
(4)/
解析：(1)；
(2)；
(3)；
(4).
12．答案：
解析：∵分式有意义,
∴,
∴,
故答案为：.
13．答案：
解析：对于分式和,3和6的最小公倍数是6,字母a,b,c的最高次幂的积为,
因此分式和的最简公分母是.
故答案为：.
14．答案：
解析：，
，
解得.
故答案为：.
15．答案：
解析：∵
.
.
故答案为：.
16．答案：
解析：如图所示,作点E关于的对称点,作点D关于的对称点,连接交,于点,,
∴根据两点之间线段最短可得,的值最小,
∴四边形的周长最小值为：,
∵在中,,,即是等腰直角三角形,
∴,
在中,
∵,
∴,
根据对顶角的性质可得,,,
根据对称的性质可得,,,,,
∴,,
在,中,
∵,,
∴
,
∴当四边形的周长最小时,的大小是,
故答案为：.
17．答案：(1)
(2)
解析：(1)
；
(2)
.
18．答案：(1)
(2)
解析：(1)
；
(2)
.
19．答案：详见解析
解析：证明：,,
,
在和中,
,
,
,
,
20．答案：,
解析：
,
当时,原式.
21．答案：(1)见解析
(2)见解析
解析：(1)由题意可得：点P在线段的垂直平分线与的交点,如下图：
(2)证明：连接,
∵,,
∴
∵,
∴,
∴,
∴为等边三角形.
22．答案：(1)
(2)
(3)
(4)
解析：(1)∵大正方形的面积等于两个阴影部分的面积加上两个长方形的面积,
∴；
(2)∵,
∴需要A型纸片6张,B型纸片2张,C型纸片7张,
即：,,,
∴；
(3)；
(4)由题意,得：,,
∴,
∴,
∴；
即：整个正方形的面积为.
23．答案：(1),,
(2),,
可以发现：一个两位数乘以11,乘积是一个百位数,百位数字是原两位数十位数字,各位数字是原两位数的个位数字,十位数字是原两位数的个位数字与十位数字的和
(3)过程见详解
(4)62×11,34×11,18×22,15×55,54×11
解析：(1)有共同特征的3个算式分别是：62×11,34×11,54×11,它们中都含有因数11；
(2),,,
可以发现：一个两位数乘以11,乘积是一个百位数,百位数字是原两位数十位数字,各位数字是原两位数的个位数字,十位数字是原两位数的个位数字与十位数字的和.
(3)设一个两位数是10a+b,
,
∴规律为：一个两位数乘以11,乘积是一个百位数,百位数字是原两位数十位数字,个位数字是原两位数的个位数字,十位数字是原两位数的个位数字与十位数字的和.
(4)∵,,
∴所有可以应用(或经过转化可以应用)上述规律的算式有：62×11,34×11,18×22,15×55,54×11.
24．答案：数据计算：,,
实验结论：三
推广证明：见解析
解析：数据计算：
方案一,漂洗后衣服中存有的污物是原来的,
方案二,漂洗后衣服中存有的污物是原来的,
方案三,漂洗后衣服中存有的污物是原来的,
故答案为：,,；
实验结论：
,
方案三的漂洗效果最好,
故答案为：三；
推广证明：
依题意可得,
选择方案一进行一次漂洗后,衣服中存有的污物是原来的,可化为；
选择方案二进行两次漂洗后,衣服中存有的污物是原来的,整理得；
选择方案三进行两次漂洗后,衣服中存有的污物是原来的,整理得；
因为三个分式的分子,分母都是正数,且分子相同,
所以要判断三个分式值的大小,只需比较分母的大小,
因为,且,,
所以,
所以,
所以,
即方案二比方案一的漂洗效果好,
因为,且,
所以,
所以,
所以,
即方案三比方案二的漂洗效果好,
综上,在这三种方案中,方案三的漂洗效果最好.
25．答案：(1)1
(2)为等腰直角三角形,详见解析
(3)的周长不变,为4,详见解析
解析：(1)过点P分别作,,的垂线,垂足分别为E、F、M,如图
,,,
,,,
,
,
,
∵,
∴,
∴
.
(2)如图.延长交y轴于点R,作于S,于T,
点C是垂直平分线上的点,
,
,
,
,
,
到,,的距离均为1,
,,分别平分,,,
,
,
于S,于T,平分,
,
,
,
,
,
,
为等腰直角三角形,且.
(3)的周长不变,为4,理由如下：
过点P分别作垂线,,,,连,.
将沿所在直线翻折,
,
,
,,
,,
的周长为,
,,
,
的周长为4.