2024-2025学年陕西省商洛市高二上学期期中考试数学检测试题（附解析）

这是一份2024-2025学年陕西省商洛市高二上学期期中考试数学检测试题（附解析），共15页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共8小题）
1．直线的倾斜角为（ ）
A．30°B．60°C．120°D．150°
2．抛物线的焦点坐标为（ ）
A．B．C．D．
3．圆和圆的位置关系是（ ）
A．相离B．外切C．内切D．相交
4．在空间四边形中，，分别为，的中点，，，，，则（ ）
A．B．
C．D．
5．已知点是双曲线：的渐近线上在第一象限内的一点，为的左焦点，则直线斜率的取值范围为（ ）
A．B．C．D．
6．在直三棱柱中，，，，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
7．已知点在直线上，那么的最小值为（ ）
A．B．C．D．2
8．已知，为椭圆的两个焦点，、为C上关于坐标原点对称的两点，且，则四边形的面积为（ ）
A．10B．8C．24D．
二、多选题（本大题共3小题）
9．如图，已知正方体的棱长为1，则（ ）

A．
B．平面
C．平面与平面的夹角为
D．点到平面的距离为
10．已知方程表示的曲线为，则（ ）
A．当时，曲线表示椭圆
B．存在，使得表示圆
C．当或时，曲线表示双曲线
D．若曲线表示焦点在轴上的椭圆，则焦距为
11．已知圆，点是圆上的点，直线，则（ ）
A．直线与圆相交所得弦长是
B．的最大值是
C．圆上恰有个点到直线的距离等于
D．过点向圆引切线，为切点，则最小值为
三、填空题（本大题共3小题）
12．平行线与间的距离为 ．
13．设、、，，，，且，，则 .
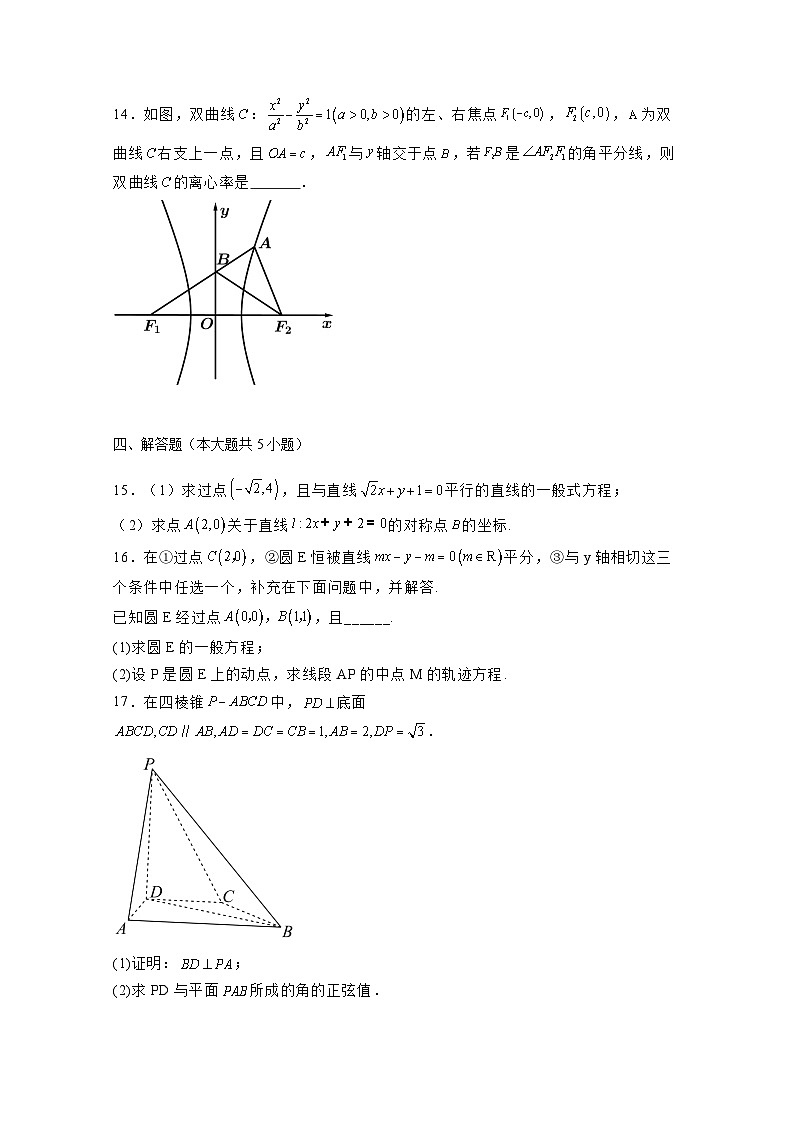
14．如图，双曲线：的左、右焦点，，为双曲线右支上一点，且，与轴交于点，若是的角平分线，则双曲线的离心率是 ．
四、解答题（本大题共5小题）
15．（1）求过点，且与直线平行的直线的一般式方程；
（2）求点关于直线的对称点的坐标.
16．在①过点，②圆E恒被直线平分，③与y轴相切这三个条件中任选一个，补充在下面问题中，并解答.
已知圆E经过点，且______.
(1)求圆E的一般方程；
(2)设P是圆E上的动点，求线段AP的中点M的轨迹方程.
17．在四棱锥中，底面．
(1)证明：；
(2)求PD与平面所成的角的正弦值．
18．已知中心在原点，焦点在轴上的椭圆与双曲线有共同的焦点、，，的长半轴与的实半轴之差为，离心率之比为.
(1)求这两条曲线的方程；
(2)求曲线以点为中点的弦所在直线的方程；
(3)若为两条曲线的交点，求的余弦值.
19．已知椭圆的离心率为，焦距为.
(1)求椭圆的标准方程；
(2)若直线与椭圆相交于、两点，且.
（i）试求、的关系式；
（ii）证明：的面积为定值.
答案
1．【正确答案】A
【详解】直线的斜率为，所以倾斜角为30°.
故选A.
2．【正确答案】C
【详解】解：将方程化为标准方程为，
所以其焦点坐标为.
故选：C
3．【正确答案】D
【详解】由，则，半径，
由，则，半径，
所以，即两圆相交.
故选D.
4．【正确答案】D
【分析】根据空间向量的线性运算法则进行运算即可.
【详解】
．
故选：D
5．【正确答案】A
【详解】由题意知，，，
故的过第一象限的渐近线斜率为，且，
又与原点连线的斜率为0，故斜率的取值范围为．
故选：A．
6．【正确答案】B
【详解】

以为坐标原点，向量方向分别为轴，建立空间直角坐标系，
则，
所以，，
所以异面直线与所成角的余弦值等于
.
故选：B
7．【正确答案】C
【分析】将用表示，根据二次函数的性质即可得结果.
【详解】由点在直线上可知，
，
当时取得最小值5，
故选：C.
8．【正确答案】B
【详解】椭圆中，，
因为、为C上关于坐标原点对称的两点，所以，
又，故四边形为平行四边形，
又，故四边形为矩形，即⊥，
由勾股定理得①，
由椭圆定义得②，
式子②平方得，
结合①得，
故四边形的面积为.
故选：B
9．【正确答案】ACD
【分析】根据正方体性质可利用线面垂直判定定理证明平面，由线面垂直性质可知A正确；易知平面即为平面，显然与平交于点，即B错误；根据二面角的定义可知即二面角的平面角为，即C正确；利用等体积法即可求得点到平面的距离为，可得D正确.
【详解】连接，如下图所示：

对于A，由正方体性质可知，平面，又平面，所以；
又因为是正方形，所以，
又，且平面，所以平面；
平面，所以可得，即A正确；
对于B，平面即为平面，又平面，
即与平交，所以B错误；
对于C，平面平面，易知，，
所以即为平面与平面夹角的平面角，显然，
即平面与平面的夹角为，可知C正确；
对于D，易知三棱锥与三棱锥的体积相等，
设点到平面的距离为，
即，可得，所以；
即点到平面的距离为，可得D正确.
故选：ACD
10．【正确答案】BC
【详解】A、B选项：当时，，，当时，，
此时曲线表示圆，A选项错误，B选项正确；
C选项：当时，，，曲线表示焦点在轴上的双曲线，
当时，，，曲线表示焦点在轴上的双曲线，C选项正确；
D选项：若曲线表示焦点在轴上的椭圆，则，则，
则椭圆的焦距，D选项错误；
故选：BC.
11．【正确答案】CD
【详解】

如图所示，
由已知圆，则圆心O0,0，半径，
A选项：圆心到直线的距离，
则弦长为，A错；
B选项：可表示点Px0,y0与点连线的斜率，
易知当直线与圆相切时，斜率取得最值，
设斜率，则直线，即，
则，解得，
所以，其最大值为，B错；
C选项：，，所以圆上恰有个点到直线的距离等于，正确；
D选项：由圆可知圆心，半径，
由切线长可知，
所以当取得最小值时，取最小值，
又，即的最小值为，
所以的最小值为，D选项正确；
故选：CD.
12．【正确答案】/
【分析】利用平行线间的距离公式计算可得答案.
【详解】将方程两边乘以2，得，
所以两平行线间的距离为．
故．
13．【正确答案】
【详解】因为、、，，，，且，，
则，解得，则，
由可得，解得，，则，
所以，因此.
故答案为.
14．【正确答案】
【详解】解：由为的中点，且，，
可得，
因为是的角平分线，
即有，，
由双曲线的定义可得，
则，
即有在直角三角形中，，
即，
由，可得，
解得或，
由于，则．
故．
15．【正确答案】（1）；（2）.
【详解】（1）根据题意，设所求直线方程为，
将点的坐标代入所求直线方程可得，解得，
故所求直线方程为；
（2）设点，由题意可知，，线段的中点在直线上，且直线的斜率为，
所以，，解得，故点的坐标为.
16．【正确答案】(1)
(2)
【分析】（1）选择①③时，设圆的一般式方程或者标准方程，代入点以及相关条件，根据待定系数法，即可确定圆的方程，选择②时，根据几何法确定圆心和半径即可求解，
（2）根据相关点法即可求解轨迹方程.
【详解】（1）方案一：选条件①.
设圆的方程为，
则，解得，
则圆E的方程为.
方案二：选条件②.
直线恒过点.
因为圆E恒被直线平分，所以恒过圆心，
所以圆心坐标为，
又圆E经过点，所以圆的半径r＝1，所以圆E的方程为，即.
方案三：选条件③.
设圆E的方程为.
由题意可得，解得，
则圆E的方程为，即.
（2）设.
因为M为线段AP的中点，所以，
因为点P是圆E上的动点，所以，即，
所以M的轨迹方程为.
17．【正确答案】(1)证明见解析；
(2).
【分析】（1）作于，于，利用勾股定理证明，根据线面垂直的性质可得，从而可得平面，再根据线面垂直的性质即可得证；
（2）以点为原点建立空间直角坐标系，利用向量法即可得出答案.
【详解】
（1）
证明：在四边形中，作于，于，
因为，
所以四边形为等腰梯形，
所以，
故，，
所以，
所以，
因为平面，平面，
所以，
又，
所以平面，
又因为平面，
所以；
（2）
解：如图，以点为原点建立空间直角坐标系，
，
则，
则，
设平面的法向量，
则有，可取，
则，
所以与平面所成角的正弦值为.
18．【正确答案】(1)，
(2)
(3)
【详解】（1）设椭圆方程为，双曲线方程为，.
则，解得，，则，，
因此，椭圆方程为，双曲线方程为.
（2）曲线以点为中点的弦的两端点分别为、，
则，，
若轴，则线段的中点在轴上，不合乎题意，
因为，这两个等式作差可得，
所以，，可得，
所以，直线的方程为，即，
检验：联立可得，则，合乎题意，
因此，曲线以点为中点的弦所在直线的方程为.
（3）不妨设、分别为两曲线的左、右焦点，是两曲线在第一象限的交点，
设，，由椭圆和双曲线的定义可得，解得，
所以，.
19．【正确答案】(1)
(2)（i）；（ii）证明见解析.
【详解】（1）因为椭圆的离心率为，故，
又焦距为，故，即有，，则，
所以，椭圆的方程为.
（2）（i）联立，消去，可得，
，
设、，则，，
故，
则，化简得；
（ii）因为，
又点到直线的距离，
所以，的面积
，
故的面积为.