2025届高考数学二轮专题复习与测试专题4圆锥曲线中的范围最值与探索课件

这是一份2025届高考数学二轮专题复习与测试专题4圆锥曲线中的范围最值与探索课件，共49页。
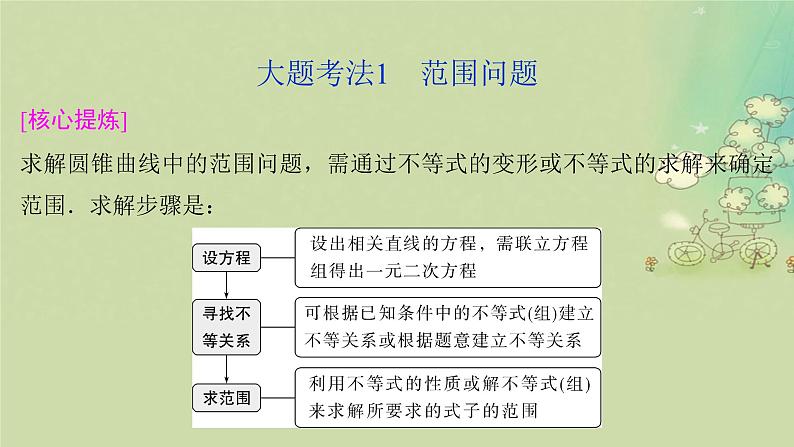
大题考法1　范围问题[核心提炼]求解圆锥曲线中的范围问题，需通过不等式的变形或不等式的求解来确定范围．求解步骤是：
圆锥曲线中的取值范围问题的求解方法(1)函数法：用其他变量表示参数，建立函数关系，利用求函数值域的方法求解．(2)不等式法：根据题意建立含参数的不等式，通过解不等式求参数的取值范围．(3)判别式法：建立关于某变量的一元二次方程，利用判别式Δ求参数的取值范围．(4)数形结合法：研究参数所表示的几何意义，利用数形结合思想求解．
大题考法2　最值问题[核心提炼]若所求圆锥曲线的最值与已知条件具有比较明确的关系，则可以考虑建立目标函数，再通过研究函数的单调性、图象或基本不等式等来解决．求解步骤是：
圆锥曲线中最值问题的两种基本解法
(2024·泰安模拟)已知直线l：kx－y－k＝0分别与x轴、直线x＝－1交于点A，B，点P是线段AB的垂直平分线上的一点(P不在x轴负半轴上)且tan ∠ABP＝|k|.(1)求点P的轨迹C的方程；
解：直线l：kx－y－k＝0，过定点A(1，0)，由题意k≠0，如图，因为tan ∠ABP＝|k|，所以∠ABP＝∠OAB，又因为P不在x轴负半轴上，所以PB与直线x＝－1垂直，又因为|PB|＝|PA|，所以点P的轨迹是以A(1，0)为焦点，x＝－1为准线的抛物线，所以点P的轨迹C的方程为y2＝4x(x≠0).
大题考法3　探索问题[核心提炼]圆锥曲线中的是否存在问题一般采用假设存在法破解，即先假设所探究的元素存在，在这个假设下探究其是否符合题目中所给信息，从而得到结论．解决问题的步骤为：
探索性问题的求解策略(1)若给出问题的一些特殊关系，要探索一般规律，并证明所得规律的正确性，通常要对已知关系进行观察、比较、分析，然后概括一般规律．(2)若只给出条件，求“不存在”“是否存在”等语句表述问题时，一般先对结论给出肯定的假设，然后由假设出发，结合已知条件进行推理，从而得出结论．
(2)是否存在直线AB，使得点P到直线AB的距离最大？若存在，求出直线AB的方程，若不存在，请说明理由．