2024-2025学年北京市高二上册期中数学检测试卷（含解析）

这是一份2024-2025学年北京市高二上册期中数学检测试卷（含解析），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．如图，E，F分别是长方体的棱AB，CD的中点，则等于（ ）
A．B．C．D．
2．直线的倾斜角为（ ）
A．B．C．D．
3．已知圆锥的母线长为5，底面圆的半径为3，则该圆锥的体积为（ ）
A．B．C．D．
4．在空间直角坐标系中，点关于轴的对称点为，则（ ）
A．B．C．D．4
5．已知，是两条不同的直线，，是两个不同的平面，则下列命题正确的是（ ）
A．若，，则B．若，l//m，则
C．若，，则D．若，α//β，则
6．已知向量，，，若，，共面，则等于（ ）
A．B．C．5D．9
7．在正方体中，直线与直线所成角的大小为（ ）
A．B．C．D．
8．已知平面，，直线，如果，且，，，则是的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
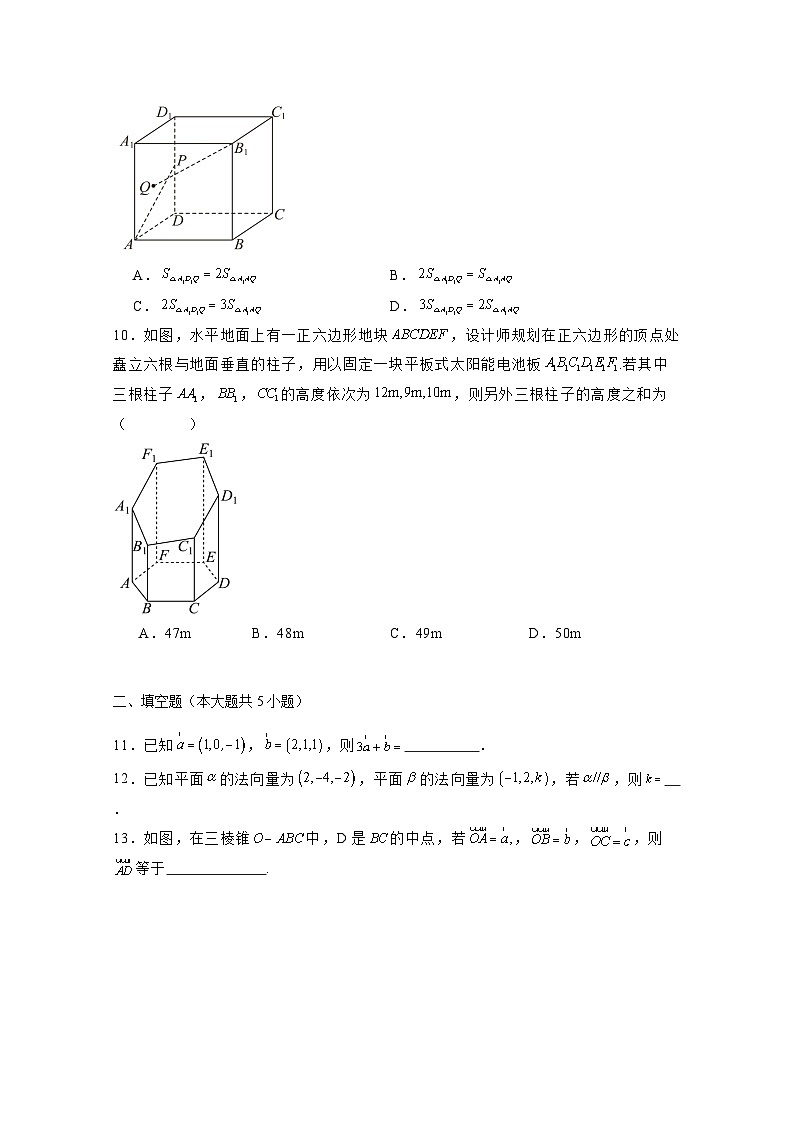
9．如图，在正方体中，点P为棱的中点，点Q为面内一点，，则（ ）
A．B．
C．D．
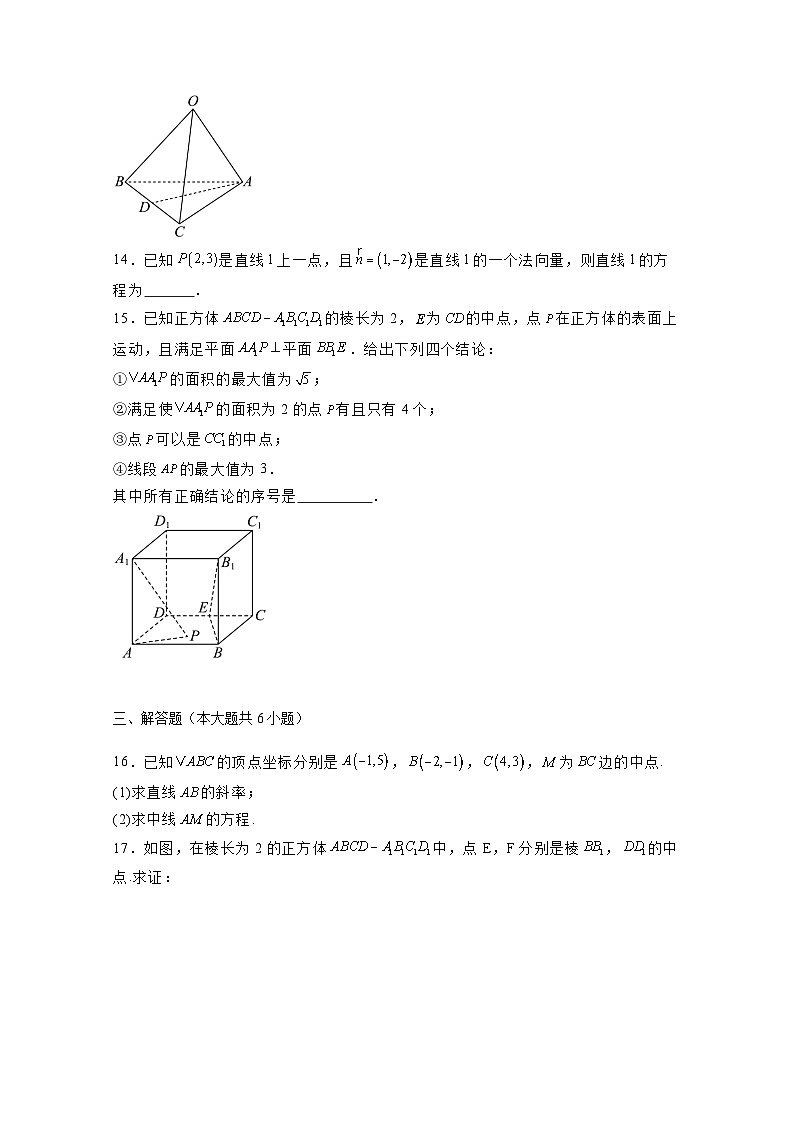
10．如图，水平地面上有一正六边形地块，设计师规划在正六边形的顶点处矗立六根与地面垂直的柱子，用以固定一块平板式太阳能电池板.若其中三根柱子，，的高度依次为，则另外三根柱子的高度之和为（ ）
A．47mB．48mC．49mD．50m
二、填空题（本大题共5小题）
11．已知，，则 ．
12．已知平面的法向量为，平面的法向量为，若，则 ．
13．如图，在三棱锥中，D是的中点，若，，，则等于 .
14．已知是直线l上一点，且是直线l的一个法向量，则直线l的方程为 ．
15．已知正方体的棱长为2，为的中点，点在正方体的表面上运动，且满足平面平面．给出下列四个结论：
①的面积的最大值为；
②满足使的面积为2的点有且只有4个；
③点可以是的中点；
④线段的最大值为3．
其中所有正确结论的序号是 ．
三、解答题（本大题共6小题）
16．已知的顶点坐标分别是，，，为边的中点.
(1)求直线的斜率；
(2)求中线的方程.
17．如图，在棱长为2的正方体中，点E，F分别是棱，的中点.求证：
(1)∥平面；
(2)平面.
18．如图，在四棱锥中，平面，，底面是边长为的正方形，E，F分别为PB，PC的中点．

(1)求证：平面ADE⊥平面PCD；
(2)求直线BF与平面ADE所成角的正弦值．
19．如图，在四棱锥中，平面，底面是直角梯形，，，，，点是的中点，直线交平面于点.

(1)求证：点是的中点；
(2)求二面角的大小
(3)求点到平面的距离.
20．在三棱锥中，平面平面，为等腰直角三角形，，，，为的中点.
(1)求证：；
(2)求二面角的余弦值；
(3)在线段上是否存在点使得平面平面？若存在，求出的值，若不存在，说明理由.
21．个有次序的实数所组成的有序数组称为一个维向量，其中称为该向量的第个分量．特别地，对一个维向量，若，称为维信号向量．设，则和的内积定义为，且．
(1)直接写出4个两两垂直的4维信号向量．
(2)证明：不存在14个两两垂直的14维信号向量．
(3)已知个两两垂直的2024维信号向量满足它们的前个分量都是相同的，求证：．
答案
1．【正确答案】D
【详解】解：=，所以D正确，A，B，C错误.
故选：D
2．【正确答案】D
【详解】直线可化为.
斜率为-1，所以倾斜角为.
故选:D.
3．【正确答案】A
【详解】设圆锥的高为,母线长为,底面半径为
画出立体图像,如图:
根据立体图形可得:
根据圆锥的体积计算公式:
故选:A.
4．【正确答案】A
【详解】因为点关于轴的对称点,
所以，
故选：A.
5．【正确答案】D
【详解】对于A:若,则可能，A错误；
对于B:若,则可能,B错误；
对于C:若则可能不垂直，C错误；
对于D:若,则,D正确.
故选：D.
6．【正确答案】D
【详解】由于共面，所以存在，使得，即
，
所以，解得：，所以.
故选：D.
7．【正确答案】C
【分析】作出辅助线，得到或其补角为直线与直线所成角，根据为等边三角形，故，得到答案.
【详解】连接，因为，，
所以四边形为平行四边形，
则，故或其补角为直线与直线所成角，
连接，则，
即为等边三角形，故，
直线与直线所成角大小为.
故选C.
8．【正确答案】B
【详解】如图，若，且，，，可得，但，
若，且，，，由线面垂直的性质定理可得，
所以是的必要不充分条件.
故选：B.
9．【正确答案】A
【详解】如图，以点为原点建立空间直角坐标系，
不妨设正方体的棱长为，
则，设，
故，
因为，
所以，即，
所以，
则点到直线的距离为，
点到直线的距离为，
所以，
故，，
所以.
故选：A.
10．【正确答案】A
【详解】依题意可知六点共面，
设正六边形的中心为，连接，
平面且平面，
依题意可知相交于，
连接交于，连接交于，
根据正六边形的性质可知四边形是菱形，所以相互平分，
则相互平分，根据梯形中位线有，
即，
在梯形中，是的中点，则是的中点，
所以，
同理可得，
所以.
故选：A
11．【正确答案】
【详解】因为，，
所以.
故答案为.
12．【正确答案】
【详解】因为，
所以两平面的法向量共线，
所以存在唯一实数，使得，
所以，解得，
所以.
故答案为.
13．【正确答案】
【详解】由图可得.
故答案为.
14．【正确答案】
【详解】因为是直线的法向量，
所以直线的斜率，
又点是直线上点，所以直线的方程为，
整理得.
故答案为.
15．【正确答案】①④
【详解】取的中点为，连接，
因为为的中点，所以，，，
所以，所以，又，
所以，所以，
又平面，又平面，所以，
又，平面，所以平面，
平面，所以平面平面，又平面平面，
所以的轨迹为线段，
对于①，由图可知，当在上时，此时三角形面积最大，
因为，所以面积的最大值为，故①正确；
对于②，由图可知，当或时，的面积为2，
所以满足使的面积为2的点有且只有2个，故②错误；
对于③，由图易知，点不可能在线段上，所以点不可能是的中点，故③错误；
对于④, 由图易知，当与重合时，此时长度最大，最大值为，故④正确.
故①④.
16．【正确答案】(1)；
(2).
【详解】（1）直线的斜率.
（2）依题意，边的中点M1,1，则直线的斜率，
所以直线的方程是，即.
17．【正确答案】(1)证明见解析
(2)证明见解析
【详解】（1）因为E，F分别为，的中点，，，
则且，可知四边形为平行四边形，则，
且平面，平面，
所以∥平面.
（2）因为四边形为正方形，则，
且，则，
又因为平面，平面，则.
且，则，
且，平面，所以平面.
18．【正确答案】(1)证明见解析
(2)
【详解】（1）平面，且平面，，
在正方形中，易知，
，且平面，平面，
平面，平面平面.
（2）以点为原点，分别以所在直线为轴，建立空间直角坐标系，如下图：

则，，，，，
由分别为的中点，则，，
取直线的方向向量为，
在平面内，取向量，，
设平面的法向量，
则，，令，则，
故平面的一个法向量，
设直线与平面的夹角为，
则.
19．【正确答案】(1)证明见解析
(2)
(3)
【详解】（1）因为，平面，平面，
所以平面.
因为直线交平面于点.
所以平面平面，平面，
所以，所以.
因为点是的中点，所以点是的中点.
（2）因为平面，平面,
所以，.
因为，
所以，，两两相互垂直.
如图，以点为坐标原点，建立空间直角坐标系.

则，，，，，
所以，.
所以，.
设平面的法向量为，
则，即
令，于是，，所以.
又因为平面的法向量为.
所以.
由题知，二面角是钝角，
所以二面角的大小为.
（3）设点到平面的距离为d，
因为，则.
20．【正确答案】(1)证明见解析
(2)
(3)存在，
【详解】（1）若为中点，连接、，又M为AB的中点.
∴，由，则，
又△为等腰直角三角形，，易知：，
由，则面，
∵面，
∴.
（2）由（1）可构建以为原点，为x、y、z轴正方向的空间直角坐标系，
∴，则，，，
若为面的一个法向量，则，令，即，
若为面的一个法向量，则，令，即，
∴，
由图可知二面角为锐角，则二面角的余弦值为.
（3）若存在N使得平面平面，且，，
由（2）知：，，则，，
若是面的一个法向量，则，令，则，
∴，可得.
∴存在N使得平面平面，此时.
21．【正确答案】(1)
(2)证明见解析
(3)证明见解析
【详解】（1）解：根据题意，结合维向量的定义，
则两两垂直的4维信号向量可以为：．
（2）解：假设存在14个两两垂直的14维信号向量，
因为将这14个向量的某个分量同时变号或将某两个位置的分量同时互换位置，任意两个向量的内积不变，
所以，不妨设，
因为，所以有7个分量为，
设的前7个分量中有个，则后7个分量中有个，
所以，可得，矛盾，
所以不存在14个两两垂直的14维信号向量．
（3）解：任取，计算内积，将所有这些内积求和得到，
则，
设的第个分量之和为，
则从每个分量的角度考虑，每个分量为的贡献为
所以，
令所以，所以．