第32讲 锐角三角函数及其应用（讲义）-2025年中考数学一轮复习讲义（含练习）

这是一份第32讲 锐角三角函数及其应用（讲义）-2025年中考数学一轮复习讲义（含练习），文件包含第32讲锐角三角函数及其应用讲义教师版docx、第32讲锐角三角函数及其应用讲义学生版docx等2份试卷配套教学资源，其中试卷共134页， 欢迎下载使用。
TOC \ "1-3" \n \h \z \u \l "_Tc157927020" 一、考情分析
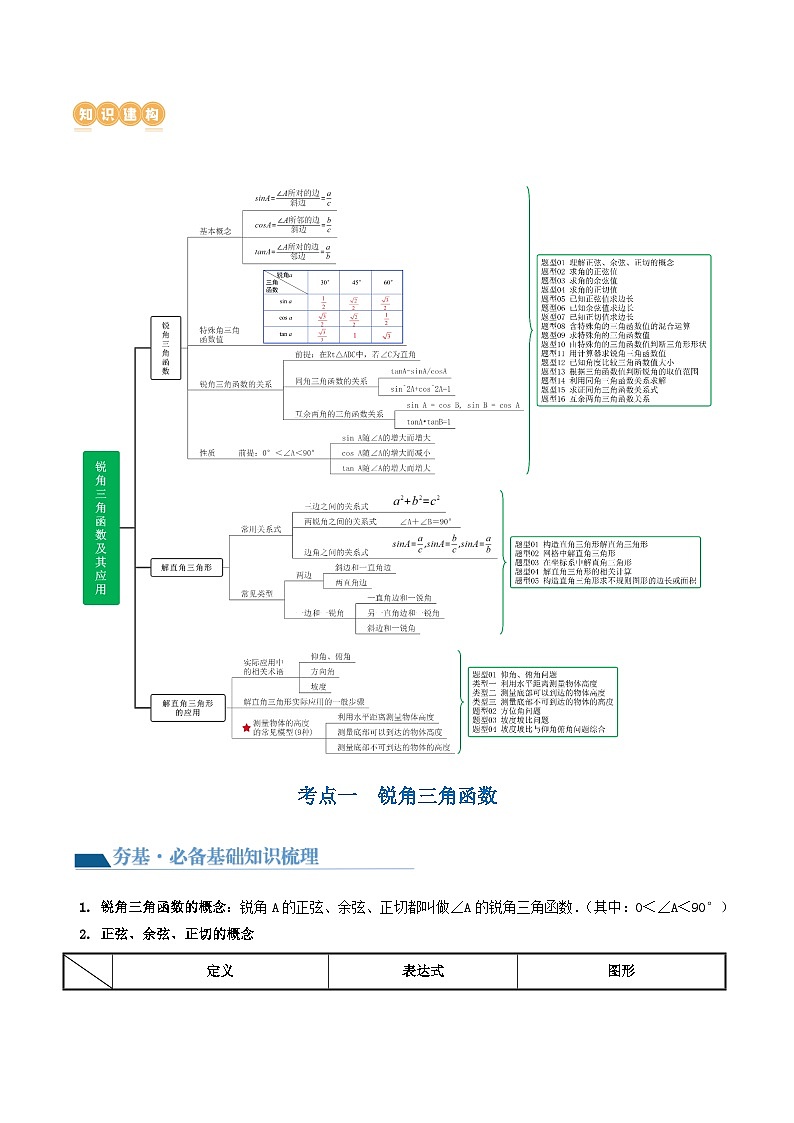
二、知识建构
\l "_Tc157927021" 考点一 锐角三角函数
\l "_Tc157927022" 题型01 理解正弦、余弦、正切的概念
\l "_Tc157927023" 题型02 求角的正弦值
\l "_Tc157927024" 题型03 求角的余弦值
\l "_Tc157927025" 题型04 求角的正切值
\l "_Tc157927026" 题型05 已知正弦值求边长
\l "_Tc157927027" 题型06 已知余弦值求边长
\l "_Tc157927028" 题型07 已知正切值求边长
\l "_Tc157927029" 题型08 含特殊角的三角函数值的混合运算
\l "_Tc157927030" 题型09 求特殊角的三角函数值
\l "_Tc157927031" 题型10 由特殊角的三角函数值判断三角形形状
\l "_Tc157927032" 题型11 用计算器求锐角三角函数值
\l "_Tc157927033" 题型12 已知角度比较三角函数值大小
\l "_Tc157927034" 题型13 根据三角函数值判断锐角的取值范围
\l "_Tc157927035" 题型14 利用同角三角函数关系求解
\l "_Tc157927036" 题型15 求证同角三角函数关系式
\l "_Tc157927037" 题型16 互余两角三角函数关系
\l "_Tc157927038" 考点二 解直角三角形
\l "_Tc157927039" 题型01 构造直角三角形解直角三角形
\l "_Tc157927040" 题型02 网格中解直角三角形
\l "_Tc157927041" 题型03 在坐标系中解直角三角形
\l "_Tc157927042" 题型04 解直角三角形的相关计算
\l "_Tc157927043" 题型05 构造直角三角形求不规则图形的边长或面积
\l "_Tc157927044" 考点三 解直角三角形的应用
\l "_Tc157927045" 题型01 仰角、俯角问题
\l "_Tc157927046" 类型一 利用水平距离测量物体高度
\l "_Tc157927047" 类型二 测量底部可以到达的物体高度
\l "_Tc157927048" 类型三 测量底部不可到达的物体的高度
\l "_Tc157927049" 题型02 方位角问题
\l "_Tc157927050" 题型03 坡度坡比问题
\l "_Tc157927051" 题型04 坡度坡比与仰角俯角问题综合
考点一 锐角三角函数
1. 锐角三角函数的概念：锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数．（其中：0＜∠A＜90°）
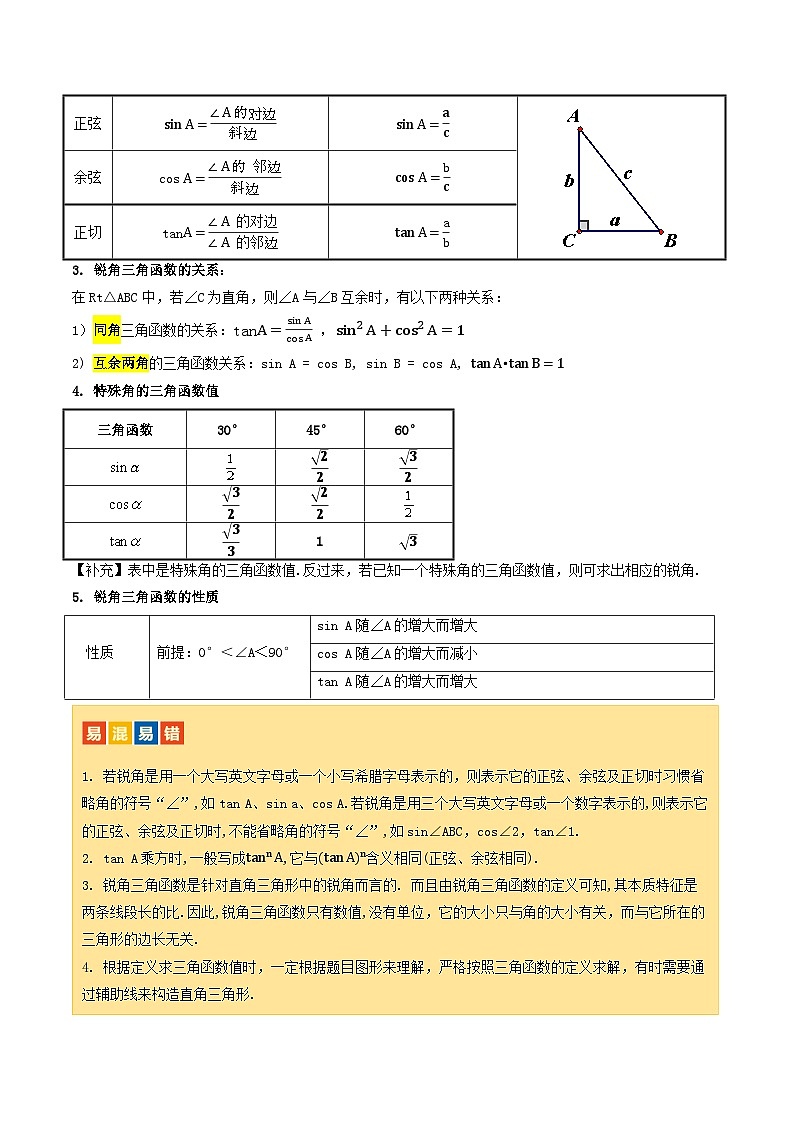
2. 正弦、余弦、正切的概念
3. 锐角三角函数的关系：
在Rt△ABC中，若∠C为直角，则∠A与∠B互余时，有以下两种关系：
1）同角三角函数的关系：tanA=sinAcsA ，sin2A+cs2A=1
2) 互余两角的三角函数关系：sin A = cs B, sin B = cs A, tanA•tanB=1
4. 特殊角的三角函数值
【补充】表中是特殊角的三角函数值.反过来，若已知一个特殊角的三角函数值，则可求出相应的锐角.
5. 锐角三角函数的性质
1. 若锐角是用一个大写英文字母或一个小写希腊字母表示的，则表示它的正弦、余弦及正切时习惯省略角的符号“∠”,如 tan A、sin a、cs A.若锐角是用三个大写英文字母或一个数字表示的,则表示它的正弦、余弦及正切时,不能省略角的符号“∠”,如sin∠ABC，cs∠2，tan∠1.
2. tan A乘方时,一般写成tannA,它与tanAn含义相同(正弦、余弦相同).
3. 锐角三角函数是针对直角三角形中的锐角而言的. 而且由锐角三角函数的定义可知,其本质特征是两条线段长的比.因此,锐角三角函数只有数值,没有单位，它的大小只与角的大小有关，而与它所在的三角形的边长无关.
4. 根据定义求三角函数值时，一定根据题目图形来理解，严格按照三角函数的定义求解，有时需要通过辅助线来构造直角三角形.
题型01 理解正弦、余弦、正切的概念
【例1】（2022·湖北·统考模拟预测）如图，在Rt△ABC中，BD是斜边AC上的高，AB≠BC，则下列比值中等于sinA的是（ ）．
A．ADABB．BDADC．BDBCD．DCBC
【变式1-1】（2021·浙江杭州·统考一模）在△ABC中，∠C＝90°，BCAB=35，则（ ）
A．csA＝35B．sinB＝35C．tanA＝43D．tanB＝43
【变式1-2】（2023·福建泉州·统考一模）在Rt△ABC中，∠C=90°，sinA=35，则csA的值是（ ）
A．35B．34C．45D．53434
【变式1-3】（2022·河北唐山·统考二模）如图，梯子（长度不变）跟地面所成的锐角为∠α，叙述正确的是（ ）

A．sinα的值越大，梯子越陡
B．csα的值越大，梯子越陡
C．tanα的值越小，梯子越陡
D．陡缓程度与∠α的函数值无关
【变式1-4】（2021·浙江杭州·统考三模）在△ABC中，∠C＝90°，∠A、∠B、∠C的对边分别是a、b、c，下列结论正确的是（ ）
A．b＝a•sinAB．b＝a•tanAC．c＝a•sinAD．a＝c•csB
【变式1-5】（2019·湖南邵阳·校联考一模）在Rt△ABC中，∠C＝90°，各边都扩大5倍，则tanA的值（ ）
A．不变B．扩大5倍C．缩小5倍D．不能确定
【变式1-6】（2021·辽宁抚顺·统考一模）如图，在△ABC中，∠C＝90°，设∠A，∠B，∠C所对的边分别为a，b，c，则（ ）
A．c＝bsinBB．b＝csinBC．a＝btanBD．b＝ctanB
题型02 求角的正弦值
【例2】（2022·江西·模拟预测）如图，PA、PB分别与⊙O相切于点A、B，连接PO并延长与⊙O交于点C、D，若CD=12，PA=8，则sin∠ADB的值为（ ）
A．45B．35C．34D．43
【变式2-1】（2020·江苏扬州·统考模拟预测）如图，由边长为1的小正方形构成的网格中，点A，B，C都在格点上，以AB为直径的圆经过点C、D，则sin∠ADC的值为（ ）
A．21313B．31313C．23D．32
【变式2-2】（2020·山东聊城·统考模拟预测）如图，在4×5的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的顶点上，那么sin∠ACB的值为（ ）．
A．355B．175C．35D．45
题型03 求角的余弦值
【例3】（2023·湖北省直辖县级单位·统考模拟预测）如图，在4×4网格正方形中，每个小正方形的边长为1，顶点为格点，若△ABC的顶点均是格点，则cs∠BAC的值是（ ）
A．55B．105C．255D．45
【变式3-1】（2022·吉林长春·校考模拟预测）如图，⊙O是△ABC的外接圆，CD是⊙O的直径．若CD=10，弦AC=6，则cs∠ABC的值为（ ）
A．45B．35C．43D．34
【变式3-2】（2023·内蒙古乌兰察布·校考模拟预测）如图，△ABC的三个顶点分别在边长为1的正方形网格上，则cs∠BAC的值为 ．
【变式3-3】（2022·广东中山·统考一模）如图，AB为⊙O的直径，点C在直径AB上（点C与A，B两点不重合），OC＝3，点D在⊙O上且满足AC＝AD，连接DC并延长到E点，使BE＝BD．
(1)求证：BE是⊙O的切线；
(2)若BE＝6，试求cs∠CDA的值．
题型04 求角的正切值
【例4】（2023·江苏扬州·统考二模）北京冬奥会开幕式的巨型雪花状主火炬塔的设计，体现了环保低碳理念．如图所示，它的主体形状呈正六边形．若点A，F，B，D，C，E是正六边形的六个顶点，则tan∠ABE＝ ．
【变式4-1】（2023·江苏苏州·校考二模）如图，AB为⊙O的直径，点C是⊙O上一点，点D是⊙O外一点，∠BCD=∠BAC，连接OD交BC于点E．
(1)求证：CD是⊙O的切线．
(2)若CE=OA,sin∠BAC=45，求tan∠CEO的值．
【变式4-2】（2022·浙江绍兴·一模）如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，连接AF交CG于点K，H是AF的中点，连接CH．
(1)求tan∠GFK的值；
(2)求CH的长．
题型05 已知正弦值求边长
【例5】（2022·云南昆明·官渡六中校考一模）在△ABC中，∠ABC=90°，若AC=100,sinA=35，则AB的长是（ ）
A．5003B．5035C．60D．80
【变式5-1】（2023·广东佛山·校联考模拟预测）如图，一辆自行车竖直摆放在水平地面上，右边是它的部分示意图，现测得∠A=88°，∠C=42°，AB=60，则点A到BC的距离为（ ）
A．60sin50°B．60sin50°C．60cs50°D．60tan50°
【变式5-2】（2020·河北·模拟预测）如图，在平面直角坐标系中，菱形OABC的边OA在x轴上，点A(10,0)，sin∠COA=45．若反比例函数y=kx(k>0,x>0)经过点C，则k的值等于（ ）
A．10B．24C．48D．50
题型06 已知余弦值求边长
【例6】（2022·广西南宁·南宁二中校考三模）如图，在△ABC中，∠C=90°,csA=32,AC=43，则AB长为（ ）
A．4B．8C．83D．12
【变式6-1】（2016·内蒙古鄂尔多斯·统考二模）如图，在△ABC中，AB＝AC＝10，点D是边BC上一动点（不与B、C重合），∠ADE＝∠B＝α，DE交AC于点E，且csα＝45，则线段CE的最大值为 ．
【变式6-2】（2020·广东广州·统考一模）如图所示，ABCD为平行四边形，AD=13，AB=25，∠DAB=α，且csα=513，点E为直线CD上一动点，将线段EA绕点E逆时针旋转α得到线段EF，连接CF．
（1）求平行四边形ABCD的面积；
（2）当点C，B，F三点共线时，设EF与AB相交于点G，求线段BG的长；
（3）求线段CF的长度的最小值．
题型07 已知正切值求边长
【例7】（2021·江苏无锡·统考一模）如图，在△ABC中，∠ABC＝90°，tan∠BAC＝12，AD＝2，BD＝4，连接CD，则CD长的最大值是（ ）
A．25+34B．25+1C．25+32D．25＋2
【变式7-1】（2023·山东日照·校考三模）如图，点A，C，D，B在⊙O上，AC＝BC，∠ACB＝90°．若CD＝a，tan∠CBD＝13，则AD的长是 ．
【变式7-2】（2023·江西萍乡·统考二模）如图，点A在第一象限，AC⊥x轴，垂足为C，OA=25，tanA=12，反比例函数y=kx的图像经过OA的中点B，与AC交于点D．
(1)求k值；
(2)求△OBD的面积．
【变式7-3】（2021·辽宁葫芦岛·统考二模）如图，已知，在△ABC中，O为AB上一点，CO平分∠ACB，以O为圆心，OB长为半径作⊙O，⊙O与BC相切于点B，交CO于点D，延长CO交⊙O于点E，连接BD，BE．
（1）求证：AC是⊙O的切线．
（2）若tan∠BDE=2，BC=6，求⊙O的半径．
题型08 含特殊角的三角函数值的混合运算
【例8】（2022·贵州·模拟预测）计算8+|-2|×cs45°的结果，正确的是（ ）
A．2B．32C．22+3D．22+2
【变式8-1】（2023·湖南株洲·校考一模）计算：12-1+12-4sin60°．
【变式8-2】（2023·山东济南·模拟预测）计算：12+3.14-π0-3tan60°+1-3+-2-2．
【变式8-3】（2023·山东聊城·统考一模）先化简，再求值：a+1-3a-1÷a2+4a+4a-1，其中a=tan45°+(12)-1-π0
题型09 求特殊角的三角函数值
【例9】（2023·山东淄博·统考一模）在实数2，x0（x≠0），cs30°，38中，有理数的个数是（ ）
A．1个B．2个C．3个D．4个
【变式9-1】（2023·广东潮州·二模）计算|1-tan60°|的值为（ ）
A．1-3B．0C．3-1D．1-33
题型10 由特殊角的三角函数值判断三角形形状
【例10】（2022·湖南衡阳·校考模拟预测）在△ABC中，∠A、∠B均为锐角，且tanB-3+2csA-32=0，则△ABC是（ ）
A．等腰三角形B．等边三角形
C．直角三角形D．等腰直角三角形
【变式10-1】（2021·广东广州·广州大学附属中学校考二模）在△ABC中，sinA=cs90°-C=22，则△ABC的形状是（ ）
A．锐角三角形B．直角三角形C．钝角三角形D．不确定
【变式10-2】（2020·四川自贡·校考一模）在△ABC中，若sinA-32+12-csB2=0，∠A，∠B都是锐角，则△ABC是 三角形．
题型11 用计算器求锐角三角函数值
【例11】（2022·山东烟台·统考一模）若用我们数学课本上采用的科学计算器计算sin36°18＇，按键顺序正确的是（ ）
A．
B．
C．
D．
【变式11-1】（2023·山东淄博·统考一模）如图，某超市计划将门前的部分楼梯改造成无障碍通道．已知楼梯共有五级均匀分布的台阶，高AB＝0.75m，斜坡AC的坡比为1：2，将要铺设的通道前方有一井盖，井盖边缘离楼梯底部的最短距离ED＝2.55m．为防止通道遮盖井盖，所铺设通道的坡角不得小于多少度？（结果精确到1）
（参考数据表）
题型12 已知角度比较三角函数值大小
【例12】（2022·上海·校考模拟预测）如果锐角A的度数是25°，那么下列结论中正确的是（ ）
A．0