广东省肇庆市广信中学、四会市四会中学等五校2024-2025学年高二上学期第二次段考数学试卷(含答案)

这是一份广东省肇庆市广信中学、四会市四会中学等五校2024-2025学年高二上学期第二次段考数学试卷(含答案)，共19页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．过，两点的直线的倾斜角是，则( )
A.2B.-2C.4D.-4
2．已知直线与.若，则( )
A.-1B.1C.D.2
3．一个平面截一球得到直径为6的圆面，球心O到这个圆面的距离为4，则这个球的体积为( )
A.B.C.D.
4．关于直线l，m及平面，，下列命题中正确的是( )
A.若，，则B.若，，则
C.若，，则D.若，，则
5．已知一个圆锥的体积为，其侧面积是底面积的2倍，则其表面积为( )
A.B.C.D.
6．圆台的高为2，体积为，两底面圆的半径比为，则母线和轴的夹角的正切值为( )
A.B.C.D.
7．如图，已知正四棱锥的所有棱长均相等，E为棱的中点，则异面直线与所成角的余弦值为( )
A.B.C.D.
8．《九章算术》中关于“刍童”（上、下底面均为矩形的棱台）体积计算的注释：将上底面的长乘以二与下底面的长相加，再与上底面的宽相乘，将下底面的长乘以二与上底面的长相加，再与下底面的宽相乘，把这两个数值相加，与高相乘，再取其六分之一现有“刍童”，其上、下底面均为正方形，若，且每条侧棱与底面所成角的正切值均为，则该“刍童”的体积为( )
A.224B.448C.D.147
二、多项选择题
9．下列说法正确的是( )
A.直线的倾斜角为
B.直线在y轴上的截距为-2
C.直线过定点
D.三条直线，，交于同一点
10．下列说法正确的是( )
A.已知空间向量，，且，则实数
B.直线与直线之间的距离是.
C.已知直线l过点，且与x，y轴正半轴交于点A，B两点，则面积的最小值为4
D.若直线l沿x轴向左平移3个单位长度，再沿y轴向上平移2个单位长度后，回到原来的位置，则该直线l的
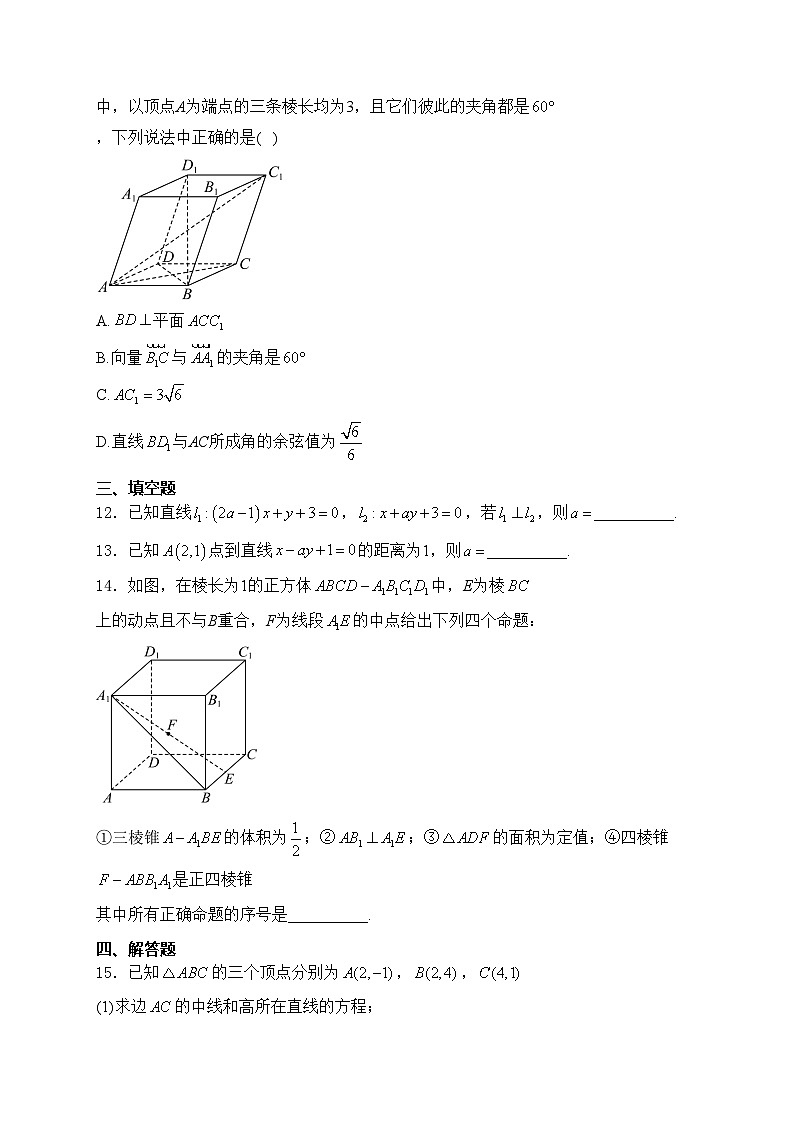
11．如图，在平行六面体中，以顶点A为端点的三条棱长均为3，且它们彼此的夹角都是，下列说法中正确的是( )
A.平面
B.向量与的夹角是
C.
D.直线与AC所成角的余弦值为
三、填空题
12．已知直线，，若，则__________.
13．已知点到直线的距离为1，则__________.
14．如图，在棱长为1的正方体中，E为棱上的动点且不与B重合，F为线段的中点给出下列四个命题：
①三棱锥的体积为；②；③的面积为定值；④四棱锥是正四棱锥
其中所有正确命题的序号是__________.
四、解答题
15．已知的三个顶点分别为，，
(1)求边的中线和高所在直线的方程；
(2)若直线l过顶点A，且原点到直线l的距离为2，求直线l的方程
16．如图，垂直于梯形所在平面，，F为的中点，，，四边形为矩形
(1)求证：平面；
(2)求点F到直线的距离；
(3)求平面与平面夹角的余弦值
17．如图，在四棱锥中，，，，，底面为正方形，M，N分别为，的中点
(1)求点B到平面的距离；
(2)求直线与平面所成角的余弦值
18．已知圆心为C的圆经过，两点，且圆心C在直线上
(1)求圆C的标准方程；
(2)点P在圆C上运动，求的取值范围
19．在中，，，，D，E分别是，上的点，满足且经过的重心，将沿折起到的位置，使，M是的中点，如图所示
(1)求证：平面；
(2)在线段上是否存在点N，使平面与平面的夹角的余弦值为,若存在，求出的长度；若不存在，请说明理由
参考答案
1．答案：B
解析：因为过，两点的直线的倾斜角是，
所以，
解得.
故选：B.
2．答案：B
解析：由于，所以，
此时两直线方程分别为，
不重合，符合题意，所以.
故选：B
3．答案：C
解析：
如图，设截面圆的圆心为，
由题意可知，圆面的直径为6，则，
又，所以球的半径，
所以球的体积，
故选：C.
4．答案：C
解析：A选项：，，，则，故A选项错误；
B选项：若，，存在，l与m不一定平行，故B选项错误；
C选项：若，则，；，则，，
∴，，∴，故C选项正确；
D选项：若，，存在或，
则不成立，故D选项错误
故选：C
5．答案：B
解析：设底面半径为r，高为h，母线为l，如图所示：
则圆锥的体积，
所以，即，
又，即，
所以，
则，解得，
所以圆锥的表面积为.
故选：B.
6．答案：B
解析：设圆台上底半径为r，则下底半径为，
由题意：.
所以圆台母线和轴的夹角的正切值为：.
故选：B
7．答案：C
解析：连接，取的中点O，连接，
由题意知，，
则异面直线与所成角为（或其补角），
在中，，，
则，
则异面直线与所成角的余弦值为，
故选：C.
8．答案：B
解析：连接，交于点，
连接，交于点，连接，过C作，如图，
.
因为“刍童”上、下底面均为正方形，
且每条侧棱与底面所成角的正切值均相等，
所以底面，又，所以底面，
所以是“刍童”
其中一条侧棱与底面所成角的平面角，则，
因为，所以，
易知四边形是等腰梯形，则，
所以在中，，
则，即“刍童”的高为12，
则该刍童的体积.
故选：B.
9．答案：BCD
解析：A选项，直线的斜率为，倾斜角为，A选项错误
B选项，由直线，令，解得，所以B选项正确
C选项，由得，
由，
解得，
所以定点为，C选项正确
D选项，由
解得，，，
所以三条直线过同一点，D选项正确
故选：BCD
10．答案：ACD
解析：A选项，由于.
所以，所以A选项正确；
B选项，直线，
因此两平行直线的距离，故B错误；
C选项，由题，直线l斜率存在且不为0，
设，
令，.
因直线与x，y轴正半轴交于点A，B两点，
则，
，
则，
当且仅当，即时，等号成立，
所以面积的最小值为4，故C正确：
D选项，由题知：直线方程斜率存在，设直线方程为，
直线l沿x轴向左平移3个单位长度，再沿y轴向上平移2个单位长度后，
回到原来的位置，则，
所以，
解得，故D正确
故选：ACD
11．答案：ACD
解析：对于A，由于四边形是菱形，所以，
，
所以，即，
由于，，平面，
所以平面，故A正确
对于B，，
所以，
，
则，
所以向量与的夹角是，所以选项B错误；
对于C，由题意可知，
则
，
所以，故C正确；
对于D，设与所成角的平面角为，
因为，
所以
，
，
，
所以，所以D正确
故选：ACD.
12．答案：
解析：由题意可知，，
解得：.
故答案为：
13．答案：
解析：由题设有，
故，故.
故答案为：
14．答案：②③④
解析：对于①，三棱锥体积为，
因此三棱锥体积的最大值为，①错误；
对于②，连接，则，
又平面，平面，
则，而，
，，平面，
则平面，
又平面，因此，②正确；
对于③，设，连接，
则，，，
即F和G到的距离相等且不变，
因此的面积为定值，③正确；
对于④，由，知平面，
又为正方形，G为其中心，
因此四棱锥是正四棱锥，④正确
故答案为：②③④
15．答案：(1)
(2)或.
解析：(1)①边的中点为，又
直线的斜率为，
边上的中线所在直线的方程为，
即.
②直线的斜率为，
边上的高所在直线的斜率为-1，
边上的高所在直线的方程为，
即.
(2)①当直线l的斜率不存在时，直线l的方程为，符合题意；
②当直线l的斜率存在时，直线l的方程可设为，
即，
由题意，原点到直线l的距离为2，
即，解得，
所求直线l的方程为.
综上，所求直线l的方程为或.
16．答案：(1)证明见解析
(2)
(3)
解析：(1)证明：设，连接，
由四边形为矩形，得G为中点，
又F为中点，则，
又平面，平面，
所以平面.
(2)由垂直于梯形所在平面，，
得直线、、两两垂直，
以D为坐标原点，直线、、分别为x、y、z轴建立空间直角坐标系，
则、、、，
，，
所以，点F到直线的距离为.
(3)由(2)可知，，，
设平面的法向量，
则，
令，得，
易知平面的一个法向量，
则，
所以平面与平面的夹角的余弦值为.
17．答案：(1)
(2)
解析：(1)因为，，，，底面为正方形，
以D为原点，为x轴，为y轴，为z轴建立空间直角坐标系，
则，，，，，
因为M，N分别为，中点，
所以，，
则，，，
设平面的法向量为，
由，即，
令，则，，所以，
则，，
根据点B到平面的距离公式.
(2)首先设平面的法向量，
，，
由，即，
令，则，，所以，
设直线与平面所成角为，
则，
，，
所以，
因为，
所以，
则直线与平面所成角的余弦值.
18．答案：(1)
(2)
解析：(1)圆经过，两点，得圆心在的中垂线上，
又圆心C在直线上，
联立直线方程有，得，
即圆心坐标为，
又，
故圆C的标准方程为.
(2)设，易知，
则
（*），
因为点P在圆C上运动，则，
故（*）式可化简为，，
由得的取值范围为.
19．答案：(1)证明见解析
(2)存在，的长度为或
解析：(1)因为在中，，，且，
所以，，则折叠后，，
又，，平面，
所以平面，平面，
所以，又已知，
且，都在面内，
所以平面.
(2)由(1)知，以为x轴，为y轴，为z轴，
建立空间直角坐标系，
因为，故，
由几何关系可知，，，，
故，，，，，，
假设在线段上存在点N，使平面与平面成角余弦值为，
，，，
设，则，
，
设平面的法向量为，
则有，即
不妨令，则，，
故平面的一个法向量为，
设平面的法向量为，
则有，即
不妨令，则，，
所以平面的一个法向量为，
若平面与平面成角余弦值为，
则满足，
化简得，解得或，
即或，
故在线段上存在这样的点N，
使平面与平面成角余弦值为，
此时的长度为或.