2020-2021学年广东省广州市花都区九年级（上）期末数学试卷（含答案）

这是一份2020-2021学年广东省广州市花都区九年级（上）期末数学试卷（含答案），共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3 分）在平面直角坐标系中，点（3，﹣5）关于原点对称的点是（ ）
A．（3，﹣5）B．（﹣3，5）C．（5，﹣3）D．（﹣3，﹣5） 2．（3 分）下列事件中是必然事件的是（ ）
A．打开电视机，正在播放中央电视台的《开学第一课》B．经过有交通信号灯的路口，遇到红灯
C．任意画一个三角形，其内角和是 180° D．同位角相等
3．（3 分）二次函数 y＝（x﹣2）2+3 的图象的顶点坐标是（ ）
A．（2，3）B．（﹣2，3）C．（﹣2，﹣3）D．（2，﹣3） 4．（3 分）下列数学符号属于中心对称图形的是（ ）
A． B．C．D．
5．（3 分）已知⊙O 的半径为 6cm，点 P 是⊙O 内的一点，则线段 OP 的长度可能为（ ）
A．5cmB．6cmC．9cmD．12cm
6．（3 分）关于 x 的一元二次方程 kx2﹣4x+1＝0 有两个实数根，则 k 的取值范围是（ ）
A．k＞4B．k≤4C．k＜4 且 k≠0D．k≤4 且 k≠0
7．（3 分）如图，在 Rt△ABC 中，∠C＝90°，点 D 是 AC 上一点，DE⊥AB 于点 E，AB＝
10，BC＝6，DE＝2.4，则 AD 的长为（ ）
A．1.2B．3C．4D．5
8．（3 分）若点（x0，y0）在函数 y＝（x＜0）的图象上，且 x0y0＝﹣2，则它的图象大致是（ ）
A．B．
C． D．
9．（3 分）如图是一个以点 O 为圆心、半径为 2.5 的圆的一部分，若过圆心 O 的直线 EM 垂直于弦 CD，垂足为 M，并且 CD＝3，则 EM 为（ ）
A．3B．3.5C．4.5D．5
10．（3 分）已知二次函数 y＝﹣x2+2x+5，若 P（n，y1），Q（n﹣2，y2）是该二次函数图象上的两点，且 y1＞y2，则实数 n 的取值范围为（ ）
A．n＜﹣1B．n＜0C．n＜1D．n＜2
二、填空题（本大题共 6 小题，每小题 3 分，满分 18 分）
11．（3 分）某校九年级共有 50 名学生参加社区垃圾分类志愿者服务活动，其中男生有 30
名，女生有 20 名，若从中随机抽一名学生，恰好抽到男生的概率是．
12．（3 分）关于 x 的方程 x2﹣2x+c＝0 有一个根是 1，那么实数 c 的值是 ．
13．（3 分）如图，△DEF 与△ABC 位似，点 O 为位似中心，已知 OF：OC＝1：2，则△DEF
与△ABC 的周长之比是．
14．（3 分）如图，已知圆锥的底面半径为 3，圆锥的母线与高的夹角 θ 为 30°，则圆锥的侧面展开图的面积是．
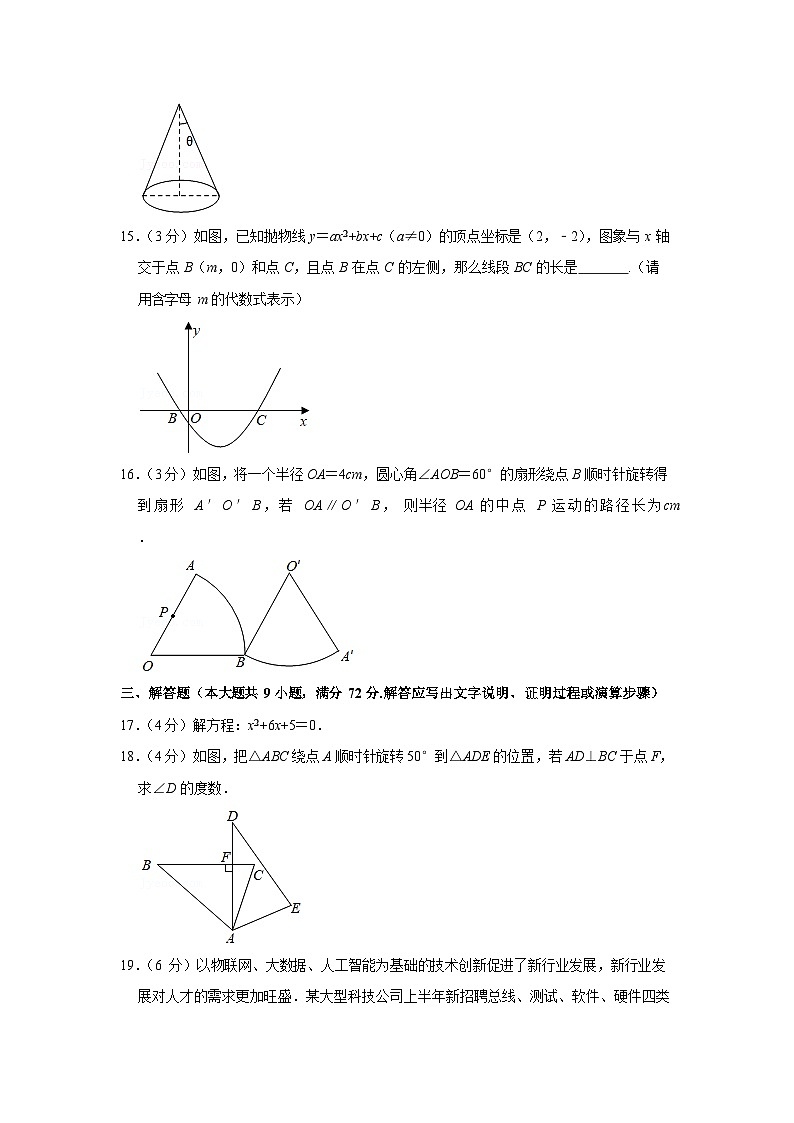
15．（3 分）如图，已知抛物线 y＝ax2+bx+c（a≠0）的顶点坐标是（2，﹣2），图象与 x 轴交于点 B（m，0）和点 C，且点 B 在点 C 的左侧，那么线段 BC 的长是.（请
用含字母 m 的代数式表示）
16．（3 分）如图，将一个半径 OA＝4cm，圆心角∠AOB＝60°的扇形绕点 B 顺时针旋转得到扇形 A ′ O ′ B ，若 OA ∥ O ′ B ， 则半径 OA 的中点 P 运动的路径长为cm．
三、解答题（本大题共 9 小题，满分 72 分.解答应写出文字说明、证明过程或演算步骤）
17．（4 分）解方程：x2+6x+5＝0．
18．（4 分）如图，把△ABC 绕点 A 顺时针旋转 50°到△ADE 的位置，若 AD⊥BC 于点 F，求∠D 的度数．
19．（6 分）以物联网、大数据、人工智能为基础的技术创新促进了新行业发展，新行业发展对人才的需求更加旺盛．某大型科技公司上半年新招聘总线、测试、软件、硬件四类
专业的毕业生共 30 人，新招聘毕业生的专业分布情况绘制成如下不完整的条形图． 请根据以上信息，解答下列问题：
“总线”专业有 人，并补全条形图；
新招聘“软件”专业的毕业生中只有两人是同校毕业，该公司从新招聘“软件”专业的毕业生中随机抽取两人参加问卷调查，求抽到两人恰好是同校毕业的概率．
20．（6 分）如图，∠MAN＝60°，点 B、C 分别在 AM、AN 上，且∠ABC＝20°．
尺规作图：作∠CBM 的角平分线 BD，BD 与 AN 相交点 D；（保留作图痕迹，不写作法）
在（1）所作的图中，求证：△ABC∽△ADB．
21．（8 分）随着国内新能源汽车的普及，为了适应社会的需求，全国各地都在加快公共充
电桩的建设，某省 2018 年公共充电桩的数量为 1 万个，2020 年公共充电桩的数量为 2.89
万个．
求 2018 年至 2020 年该省公共充电桩数量的年平均增长率；
按照这样的增长速度，预计 2021 年该省将新增多少万个公共充电桩？
22．（10 分）如图，已知四边形 ABCD，∠B＝∠D＝60°，AD 为直径的⊙O 经过点 C，AB
是⊙O 的切线，OE∥BC．
求证：BC 是⊙O 的切线；
若 AE＝1，求 BE 的长．
23．（10 分）如图，平行四边形 OABC 的顶点 A 在 y 轴的正半轴上，点 D（2，4）在对角线 OB 上，反比例函数 y＝（x＞0）的图象经过 C，D 两点．
求 m 的值；
若△BOC 的面积是 12，求点 C 的坐标．
24．（12 分）已知抛物线 y＝ax2﹣3ax+经过点 A（5，0），且与 y 轴交于点 B，点 E 在该抛物线的对称轴上运动．
求抛物线的对称轴；
若△ABE 是以 AB 为直角边的直角三角形，求点 E 的坐标；
若点 P（m，n）是抛物线上的一个动点，当点 E 运动到 x 轴上时，连接 EP，经过探究发现，随着 n 的变化，EP2 与 n 之间存在一个函数关系，求这个函数关系式，并求出 EP2 的最小值．
25．（12 分）如图 1，⊙O 为 Rt△ABC 的外接圆，∠ACB＝90°，BC＝4，AC＝4，点 D
是⊙O 上的动点，且点 C、D 分别位于 AB 的两侧．
求⊙O 的半径；
当 CD＝4时，求∠ACD 的度数；
设 AD 的中点为 M，在点 D 的运动过程中，线段 CM 是否存在最大值？若存在， 求出 CM 的最大值；若不存在，请说明理由．
2020-2021 学年广东省广州市花都区九年级（上）期末数学试卷
参考答案与试题解析
一、选择题（本大题共 10 小题，每小题 3 分，满分 30 分.在每小题给出的四个选项中，只有一项是符合题目要求的。）
1．（3 分）在平面直角坐标系中，点（3，﹣5）关于原点对称的点是（ ）
A．（3，﹣5）B．（﹣3，5）C．（5，﹣3）D．（﹣3，﹣5）
【分析】根据两个点关于原点对称时，它们的坐标符号相反可得答案．
【解答】解：点（3，﹣5）关于原点对称的点是（﹣3，5），故选：B．
【点评】此题主要考查了关于原点对称的点的坐标特点，关键是掌握：点 P（x，y）关于原点 O 的对称点是 P′（﹣x，﹣y）．
2．（3 分）下列事件中是必然事件的是（ ）
A．打开电视机，正在播放中央电视台的《开学第一课》B．经过有交通信号灯的路口，遇到红灯
C．任意画一个三角形，其内角和是 180° D．同位角相等
【分析】根据事件发生的可能性大小判断，得到答案．
【解答】解：A、打开电视机，正在播放中央电视台的《开学第一课》，是随机事件；
B、经过有交通信号灯的路口，遇到红灯，是随机事件； C、任意画一个三角形，其内角和是 180°，是必然事件； D、同位角相等，是随机事件；
故选：C．
【点评】本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
3．（3 分）二次函数 y＝（x﹣2）2+3 的图象的顶点坐标是（ ）
A．（2，3）B．（﹣2，3）C．（﹣2，﹣3）D．（2，﹣3）
【分析】根据顶点式可直接写出顶点坐标．
【解答】解：∵抛物线解析式为 y＝（x﹣2）2+3，
∴二次函数图象的顶点坐标是（2，3）．故选：A．
【点评】考查了二次函数的性质，根据抛物线的顶点式，可确定抛物线的开口方向，顶点坐标（对称轴），最大（最小）值，增减性等．
4．（3 分）下列数学符号属于中心对称图形的是（ ）
A． B．C．D．
【分析】根据中心对称图形的概念对各选项分析判断即可得解．
【解答】解：A、不是中心对称图形，故本选项不合题意；
B、是中心对称图形，故本选项符合题意； C、不是中心对称图形，故本选项不合题意； D、不是中心对称图形，故本选项不合题意． 故选：B．
【点评】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转 180
度后与原图重合．
5．（3 分）已知⊙O 的半径为 6cm，点 P 是⊙O 内的一点，则线段 OP 的长度可能为（ ）
A．5cmB．6cmC．9cmD．12cm
【分析】当⊙O 的半径是 R，点 P 到圆心 O 的距离是 d，当 d＝R 时，点 P 在⊙O 上，当
d＜R 时，点 P 在⊙O 内，当 d＞R 时，点 P 在⊙O 外，根据以上内容判断即可．
【解答】解：∵点 P 在⊙O 内，⊙O 的半径为 6cm，
∴OP＜6cm，
A、5cm＜6cm，故本选项正确；
B、6cm＝6cm，此时 P 在圆上，故本选项错误； C、9cm＞6cm，此时 P 在圆外，故本选项错误； D、12cm＞6cm，此时 P 在圆外，故本选项错误； 故选：A．
【点评】本题考查了点和圆的位置关系，注意：点 P 和圆 O 有三种位置关系：当⊙O 的半径是 R，点 P 到圆心 O 的距离是 d，①当 d＝R 时，点 P 在⊙O 上，②当 d＜R 时，点P 在⊙O 内，③当 d＞R 时，点 P 在⊙O 外．
6．（3 分）关于 x 的一元二次方程 kx2﹣4x+1＝0 有两个实数根，则 k 的取值范围是（ ）
A．k＞4B．k≤4C．k＜4 且 k≠0D．k≤4 且 k≠0
【分析】若一元二次方程有两个实数根，则根的判别式Δ＝b2﹣4ac≥0，建立关于 k 的不等式，求出 k 的取值范围．还要注意二次项系数不为 0．
【解答】解：∵方程有两个实数根，
∴根的判别式Δ＝b2﹣4ac＝16﹣4k≥0， 即 k≤4，且 k≠0．
故选：D．
【点评】本题考查了一元二次方程根的判别式的应用．切记不要忽略一元二次方程二次项系数不为零这一隐含条件．
7．（3 分）如图，在 Rt△ABC 中，∠C＝90°，点 D 是 AC 上一点，DE⊥AB 于点 E，AB＝
10，BC＝6，DE＝2.4，则 AD 的长为（ ）
A．1.2B．3C．4D．5
【分析】先△ADE∽△ABC；利用对应边成比例即可求解．
【解答】解：∵DE⊥AB，
∴∠AED＝∠C＝90°，
∵∠A＝∠A，
∴△ADE∽△ABC；
∴．
即： ．
∴AD＝4． 故选：C．
【点评】本题考查相似三角形的证明，已经相似的性质，解题的关键是熟练运用相似三角形的性质与判定，本题属于基础题．
8．（3 分）若点（x0，y0）在函数 y＝ （x＜0）的图象上，且 x0y0＝﹣2，则它的图象大致
是（ ）
A． B．
C． D．
【分析】首先由 x0y0＝﹣2，得出 k 的值，然后根据 x＜0 及反比例函数 y＝的图象性质作答．
【解答】解：因为（x0，y0）在函数 y＝（x＜0）的图象上， 所以 k＝x0y0＝﹣2＜0；
又因为 x＜0，
所以图象只在第二象限． 故选：B．
【点评】反比例函数 y＝的图象是双曲线．当 k＞0 时，它的两个分支分别位于第一、
三象限；当 k＜0 时，它的两个分支分别位于第二、四象限．解答本题时要注意，x＜0 时图象只有一个分支．
9．（3 分）如图是一个以点 O 为圆心、半径为 2.5 的圆的一部分，若过圆心 O 的直线 EM 垂直于弦 CD，垂足为 M，并且 CD＝3，则 EM 为（ ）
A．3B．3.5C．4.5D．5
【分析】连接 OC，先由垂径定理得 CM＝DM＝CD＝，再由勾股定理求出 OM＝2， 即可求解．
【解答】解：连接 OC，如图所示：
则 OC＝OE＝2.5＝，
∵EM⊥CD，
∴CM＝DM＝ CD＝ ，
由勾股定理得：OM＝＝＝2，
∴EM＝OE+OM＝2.5+2＝4.5，
故选：C．
【点评】本题考查了勾股定理、垂径定理等知识，熟练掌握垂径定理和勾股定理是解此题的关键．
10．（3 分）已知二次函数 y＝﹣x2+2x+5，若 P（n，y1），Q（n﹣2，y2）是该二次函数图象
上的两点，且 y1＞y2，则实数 n 的取值范围为（ ）
A．n＜﹣1B．n＜0C．n＜1D．n＜2
【分析】将 n，n﹣2 代入二次函数解析式即可得出 n 的取值范围．
【解答】解：∵P（n，y1），Q（n﹣2，y2）是函数 y＝﹣x2+2x+5 的图象上的两点，且 y1
＞y2，
∴﹣n2+2n+5＞﹣（n﹣2）2+2（n﹣2）+5， 化简整理得，4n﹣8＜0，
∴n＜2，
∴实数 n 的取值范围是 n＜2， 故选：D．
【点评】本题考查了二次函数的性质，二次函数图象上点的坐标特征，根据题意列出不等式是解题的关键．
二、填空题（本大题共 6 小题，每小题 3 分，满分 18 分）
11．（3 分）某校九年级共有 50 名学生参加社区垃圾分类志愿者服务活动，其中男生有 30
名，女生有 20 名，若从中随机抽一名学生，恰好抽到男生的概率是 ．
【分析】用男生的人数除以所有学生的人数的和即可求得答案．
【解答】解：∵共 50 名学生，其中男生 30 名，
∴从中随机抽一名学生，恰好抽到男生的概率是＝， 故答案为：．
【点评】此题考查概率的求法：如果一个事件有 n 种可能，而且这些事件的可能性相同，
其中事件 A 出现 m 种结果，那么事件 A 的概率 P（A）＝．
12．（3 分）关于 x 的方程 x2﹣2x+c＝0 有一个根是 1，那么实数 c 的值是 1 ．
【分析】把 x＝1 代入已知方程，列出关于 c 的一元一次方程，通过解该方程来求 c 的值．
【解答】解：∵关于 x 的方程 x2﹣2x+c＝0 有一个根是 1，
∴12﹣2×1+c＝0，即﹣1+c＝0， 解得 c＝1．
故答案是：1．
【点评】本题主要考查了一元二次方程的解的定义．方程的根即方程的解，就是能使方程左右两边相等的未知数的值．
13．（3 分）如图，△DEF 与△ABC 位似，点 O 为位似中心，已知 OF：OC＝1：2，则△DEF
与△ABC 的周长之比是 1：2 ．
【分析】直接利用位似图形的性质得出△DEF 与△ABC 的周长之比．
【解答】解：∵△DEF 与△ABC 位似，点 O 为位似中心，
∴△DEF 与△ABC 的周长之比是：1：2． 故答案为：1：2．
【点评】此题主要考查了位似变换，正确掌握位似图形的性质是解题关键．
14．（3 分）如图，已知圆锥的底面半径为 3，圆锥的母线与高的夹角 θ 为 30°，则圆锥的侧面展开图的面积是 18π ．
【分析】先利用含 30 度的直角三角形三边的关系得到圆锥的母线长为 6，由于锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长， 则利用扇形的面积公式可计算出圆锥的侧面展开图的面积．
【解答】解：∵圆锥的母线与高的夹角 θ 为 30°，底面半径为 3，
∴圆锥的母线长为 6，
∴圆锥的侧面展开图的面积＝ ×2π×3×6＝18π． 故答案为 18π．
【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
15．（3 分）如图，已知抛物线 y＝ax2+bx+c（a≠0）的顶点坐标是（2，﹣2），图象与 x 轴交于点 B（m，0）和点 C，且点 B 在点 C 的左侧，那么线段 BC 的长是 4﹣2m .（请
用含字母 m 的代数式表示）
【分析】根据抛物线的轴对称性质解答．
【解答】解：∵抛物线 y＝ax2+bx+c（a≠0）的顶点坐标是（2，﹣2），
∴抛物线的对称轴是直线 x＝2．
∵点 B（m，0）和点 C 关于直线 x＝2 对称，
∴点 C 的坐标是（4﹣m，0）．
∴BC＝4﹣m﹣m＝4﹣2m． 故答案是：4﹣2m．
【点评】本题主要考查了抛物线与 x 轴的交点，二次函数的性质，解题时，充分利用了抛物线的轴对称性质，属于中考常考题型．
16．（3 分）如图，将一个半径 OA＝4cm，圆心角∠AOB＝60°的扇形绕点 B 顺时针旋转得到扇形 A′O′B，若 OA∥O′B，则半径 OA 的中点 P 运动的路径长为 π cm．
【分析】证明△AOB 是等边三角形，求出 BP，∠PBP′，利用弧长公式求解即可．
【解答】解：连接 PB，AB．
∵OA＝OB，∠AOB＝60°，
∴△AOB 是等边三角形，
∴∠OBA＝∠OAB＝60°，
∵OP＝PA，
∴∠APB＝∠OPB＝30°，PB⊥OA，
∴PB＝OB•cs30°＝2（cm），
∵OA∥BO′，
∴∠OAB＝∠ABO′，
∴∠PBP′＝30°+60°+30°＝120°，
∴半径 OA 的中点 P 运动的路径长为＝π（cm）．
故答案为：π．
【点评】本题考查轨迹，弧长公式，平行线的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
三、解答题（本大题共 9 小题，满分 72 分.解答应写出文字说明、证明过程或演算步骤）
17．（4 分）解方程：x2+6x+5＝0．
【分析】利用因式分解法解方程．
【解答】解：（x+1）（x+5）＝0， x+1＝0 或 x+5＝0，
解得 x1＝﹣1，x2＝﹣5．
【点评】本题考查了解一元二次方程﹣因式分解法：先把方程的右边化为 0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为 0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了实数的运算．
18．（4 分）如图，把△ABC 绕点 A 顺时针旋转 50°到△ADE 的位置，若 AD⊥BC 于点 F，求∠D 的度数．
【分析】由旋转的性质可得∠B＝∠D，∠BAD＝50°，即可求解．
【解答】解：∵把△ABC 绕点 A 顺时针旋转 50°到△ADE 的位置，
∴∠B＝∠D，∠BAD＝50°，
∵AD⊥BC，
∴∠B＝40°＝∠D．
【点评】本题考查了旋转的性质，掌握旋转的性质是本题的关键．
19．（6 分）以物联网、大数据、人工智能为基础的技术创新促进了新行业发展，新行业发展对人才的需求更加旺盛．某大型科技公司上半年新招聘总线、测试、软件、硬件四类专业的毕业生共 30 人，新招聘毕业生的专业分布情况绘制成如下不完整的条形图．
请根据以上信息，解答下列问题：
“总线”专业有 8 人，并补全条形图；
新招聘“软件”专业的毕业生中只有两人是同校毕业，该公司从新招聘“软件”专业的毕业生中随机抽取两人参加问卷调查，求抽到两人恰好是同校毕业的概率．
【分析】（1）由总人数减去其它三类专业的毕业生人数得出“总线”专业人数，补全条形图即可；
（2）画树状图，共有 12 个等可能的结果，其中抽到两人恰好是同校毕业的结果有 2 个， 再由概率公式求解即可．
【解答】解：（1）总线”专业有：30﹣12﹣4﹣6＝8（人），故答案为：8；
补全条形图如图：
（2）把同校毕业的两人记为 A、A'，其他两人记为 B、C，画树状图如图：
共有 12 个等可能的结果，其中抽到两人恰好是同校毕业的结果有 2 个，
∴抽到两人恰好是同校毕业的概率为＝ ．
【点评】本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出 n，再从中选出符合事件 A 或 B 的结果数目 m，然后根据概率公式求出事件 A 或 B 的概率．也考查了条形统计图．
20．（6 分）如图，∠MAN＝60°，点 B、C 分别在 AM、AN 上，且∠ABC＝20°．
尺规作图：作∠CBM 的角平分线 BD，BD 与 AN 相交点 D；（保留作图痕迹，不写作法）
在（1）所作的图中，求证：△ABC∽△ADB．
【分析】（1）根据题意作出图形即可；
（2）根据角平分线定义和相似三角形的判定定理即可得到结论．
【解答】解：（1）如图所示，线段 BD 即为所求；
（2）∵∠ABC＝20°，
∴∠CBM＝160°，
∵BD 平分∠CBM，
∴∠CBD＝ CBM＝80°，
∴∠ADB＝180°﹣∠A﹣∠ABC﹣∠CBD＝20°，
∴∠ABC＝∠ADB，
∵∠A＝∠A，
∴△ABC∽△ADB．
【点评】本题考查了相似三角形的判定，作图﹣基本作图，角平分线定义，三角形的内角和定理，正确的作出图形是解题的关键．
21．（8 分）随着国内新能源汽车的普及，为了适应社会的需求，全国各地都在加快公共充
电桩的建设，某省 2018 年公共充电桩的数量为 1 万个，2020 年公共充电桩的数量为 2.89
万个．
求 2018 年至 2020 年该省公共充电桩数量的年平均增长率；
按照这样的增长速度，预计 2021 年该省将新增多少万个公共充电桩？
【分析】（1）设 2018 年至 2020 年该省公共充电桩数量的年平均增长率为 x，根据该省
2018 年及 2020 年公共充电桩，即可得出关于 x 的一元二次方程，解之取其正值即可得出结论；
（2）根据该省 2021 年公共充电桩数量＝该省 2020 年公共充电桩数量×增长率，即可求出结论．
【解答】解：（1）设 2018 年至 2020 年该省公共充电桩数量的年平均增长率为 x，依题意得：（1+x）2＝2.89，
解得：x1＝0.7＝70%，x2＝﹣2.7（不合题意，舍去）．
答：2018 年至 2020 年该省公共充电桩数量的年平均增长率为 70%．
（2）2.89×70%＝2.023（万个）．
答：预计 2021 年该省将新增 2.023 万个公共充电桩．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
22．（10 分）如图，已知四边形 ABCD，∠B＝∠D＝60°，AD 为直径的⊙O 经过点 C，AB
是⊙O 的切线，OE∥BC．
求证：BC 是⊙O 的切线；
若 AE＝1，求 BE 的长．
【分析】（1）由等边三角形的判定与性质得出∠DCO＝60°，由四边形内角和定理求出
∠OCB＝90°，则可得出答案；
（2）连接 OB，由切线长定理得出∠OBA＝30°，由直角三角形的性质得出 AB 的长，则可求出答案．
【解答】解：（1）连接 OC，
∵∠B＝∠D＝60°，
∴△ODC 为等边三角形，
∴∠DCO＝60°，
∵AB 是⊙O 的切线，
∴∠OAB＝90°，
∵∠A+∠B+∠C+∠BCD＝360°，
∴∠BCO＝360°﹣∠A﹣∠B﹣∠D﹣∠OCD＝360°﹣90°﹣60°﹣60°﹣60°＝
90°，
∴OC⊥BC，
∴BC 是⊙O 的切线；
（2）如图，连接 OB，
∵OE∥BC，∠ABC＝60°，
∴∠OEA＝∠ABC＝60°，
∴∠AOE＝90°﹣∠OEA＝30°，
∵AE＝1，
∴OE＝2AE＝2，
∴OA＝ ＝＝，
∵BA，BC 是⊙O 的切线，
∴∠OBA＝ ∠ABC＝30°，
∴OB＝2OA＝2 ，
∴AB＝ ＝＝3，
∴BE＝AB﹣AE＝3﹣1＝2．
【点评】本题考查了切线的判定和性质，勾股定理，平行线的性质，等边三角形的判定和性质，熟练掌握性质定理是解题的关键．
23．（10 分）如图，平行四边形 OABC 的顶点 A 在 y 轴的正半轴上，点 D（2，4）在对角线
OB 上，反比例函数 y＝（x＞0）的图象经过 C，D 两点．
求 m 的值；
若△BOC 的面积是 12，求点 C 的坐标．
【分析】（1）根据待定系数法即可求得；
（2）延长 BC，交 x 轴于 E，作 DF⊥x 轴于 F，即可得到 S△ODF＝S△OCE＝4，从而得到
△OBE 的面积为 16，通过证得△ODF∽△OBE，证得 OE＝4，把 C 的横坐标代入解析式即可求得 C 的纵坐标．
【解答】解：（1）∵反比例函数 y＝（x＞0）的图象经过点 D（2，4），
∴m﹣2＝2×4＝8，
∴m＝10；
（2）延长 BC，交 x 轴于 E，作 DF⊥x 轴于 F，
∵四边形 OABC 是平行四边形，
∴BC∥y 轴，
∵反比例函数为 y＝的图象经过 C，D 两点．
∴S△ODF＝S△OCE＝4，
∵△BOC 的面积是 12，
∴△OBE 的面积为 16，
∵点 D（2，4），
∴OF＝2，
∵DF∥BE，
∴△ODF∽△OBE，
∴＝（ ）2＝ ，
∴OE：OF＝2：1，
∴OE＝2OF＝4，
∴C 点的横坐标为 4，
把 x＝4 代入 y＝得，y＝2，
∴点 C 的坐标为（4，2）．
【点评】本题考查了反比例函数图象上点的坐标特征，反比例函数系数 k 的几何意义， 三角形相似的判定和性质，作出辅助线根据相似三角形是解题的关键．
24．（12 分）已知抛物线 y＝ax2﹣3ax+经过点 A（5，0），且与 y 轴交于点 B，点 E 在该抛物线的对称轴上运动．
求抛物线的对称轴；
若△ABE 是以 AB 为直角边的直角三角形，求点 E 的坐标；
若点 P（m，n）是抛物线上的一个动点，当点 E 运动到 x 轴上时，连接 EP，经过探究发现，随着 n 的变化，EP2 与 n 之间存在一个函数关系，求这个函数关系式，并求出 EP2 的最小值．
【分析】（1）根据对称轴 x＝﹣计算即可．
直线直线 AB 的解析式，可得 N（，），推出 BN＝，AN＝，分两种情形利用相似三角形的性质，求出 EN，NE′可得结论．
根据二次函数，利用二次函数的性质求解即可．
【解答】解：（1）抛物线的对称轴 x＝﹣＝
（2）∵抛物线 y＝ax2﹣3ax+经过点 A（5，0），
∴25a﹣15a+ ＝0，
∴a＝﹣ ，
如图 1 中，设抛物线的对称轴交 AB 于 N，交 x 轴于 T．
∵A（5，0），B（0，），
∴OB＝ ，OA＝5，
∴AB＝＝＝，
∴直线 AB 的解析式为 y＝﹣x+ ，
∵对称轴 x＝，
∴N（ ，），
∴BN＝ ＝，
∴AN＝AB﹣BN＝ ，
∵EN∥OB，
∴∠ENB＝∠ABO，
∵∠EBN＝∠AOB＝90°，
∴△EBN∽△AOB，
∴＝，
∴＝，
∴EN＝ ，ET＝TN+EN＝ ，
∴E（ ，），
当∠NAE′＝90°时，同法可得 E′N＝，ET＝7，
∴E′（，﹣7）．
综上所述，满足条件的点 E 的坐标为（ ，）或（ ，﹣7）．
（3）如图 2 中，∵P（m，n），E（，0），
∴PE2＝（m﹣ ）2+n2＝m2﹣3m+ +n2，
∵n＝﹣ m2+ m+ ，
∴m2﹣3m＝10﹣4n，
∴PE2＝10﹣4n+ +n2＝（n﹣2）2+ ，
∴PE2 的最小值为．PE2＝n2﹣4n+ ．
【点评】本题属于二次函数综合题，考查了二次函数的性质，一次函数的性质，待定系数法，相似三角形的判定和性质等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考常考题型．
25．（12 分）如图 1，⊙O 为 Rt△ABC 的外接圆，∠ACB＝90°，BC＝4，AC＝4，点 D
是⊙O 上的动点，且点 C、D 分别位于 AB 的两侧．
求⊙O 的半径；
当 CD＝4时，求∠ACD 的度数；
设 AD 的中点为 M，在点 D 的运动过程中，线段 CM 是否存在最大值？若存在， 求出 CM 的最大值；若不存在，请说明理由．
【分析】（1）利用勾股定理求出 AB 即可．
连接 OC，OD，证明∠OCA＝60°，∠OCD＝45°，可得结论．
如图 2 中，连接 OM，OC．证明 OM⊥AD，推出点 M 的运动轨迹以 AO 为直径的
⊙J，连接 CJ，JM．求出 CJ．JM，根据 CM≤CJ+JM＝2+2，可得结论．
【解答】解：（1）如图 1 中，
∵AB 是直径，
∴∠ACB＝90°，
∵AC＝4，BC＝4 ，
∴AB＝ ＝＝8，
∴⊙O 的半径为 4．
如图 1 中，连接 OC，OD．
∵CD＝4 ，OC＝OD＝4，
∴CD2＝OC2+OD2，
∴∠COD＝90°，
∴∠OCD＝45°，
∵AC＝OC＝OA，
∴△AOC 是等边三角形，
∴∠ACO＝60°，
∴∠ACD＝∠ACO﹣∠DCO＝60°﹣45°＝15°．
如图 2 中，连接 OM，OC．
∵AM＝MD，
∴OM⊥AD，
∴点 M 的运动轨迹以 AO 为直径的⊙J， 连接 CJ，JM．
∵△AOC 是等边三角形，AJ＝OJ，
∴CJ⊥OA，
∴CJ＝ ＝2 ，
∵CM≤CJ+JM＝2 +2，
∴CM 的最大值为 2+2．
【点评】本题属于圆综合题，考查了圆周角定理，垂径定理，等边三角形的判定和性质， 等腰直角三角形的判定和性质，解直角三角形等知识，解题的关键是寻找特殊三角形解决问题，正确寻找点 M 的运动轨迹，属于中考压轴题．