2025年中考数学一轮复习 -第三章 函数-第三节 一次函数的实际应用课件

这是一份2025年中考数学一轮复习 -第三章 函数-第三节 一次函数的实际应用课件，共29页。PPT课件主要包含了考点梳理，回练课本，新课标新考向等内容，欢迎下载使用。
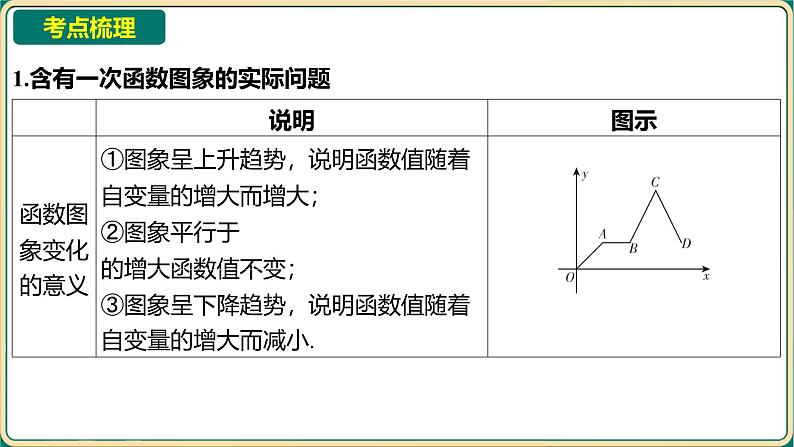
1.含有一次函数图象的实际问题
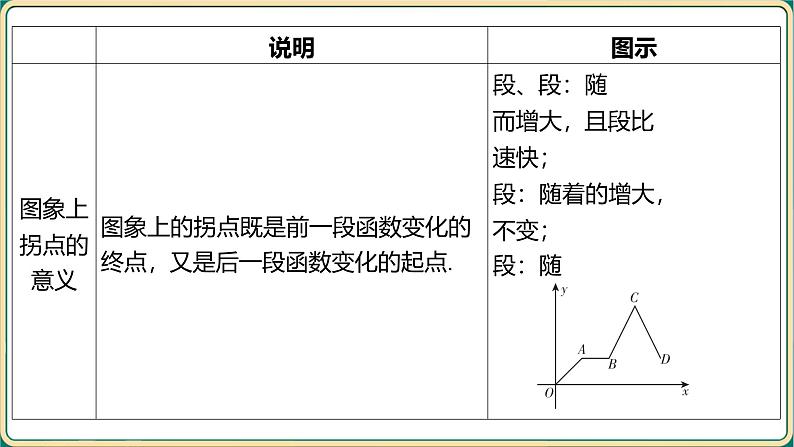
2.不含一次函数图象的实际问题（1）一般解题步骤①设出问题中的变量，弄清自变量和因变量；②建立一次函数模型（列一次函数解析式）；③确定自变量的取值范围；④利用一次函数的性质解决实际问题；⑤作答.（2）实际问题中的最大值、最小值在一次函数的实际应用题中, 根据自变量的取值范围,利用一次函数的增减性即可求出实际问题中的最值.
2.近年来，中国传统服饰备受大家的青睐，走上国际时装周舞台，大放异彩．某服装店直接从工厂购进长、短两款传统服饰进行销售，进货价和销售价如表：
若该服装店计划购进长、短两款服装共200件（进货价和销售价都不变），且进货总价不高于16 800元．则服装店应购进短款服装_____件，长款服装____件，才能获得最大销售利润，最大销售利润是_______元.
考法 一次函数的实际应用
例1 [2024长春中考] 区间测速是指在某一路段前后设置两个监控点，根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在高速公路上行驶，其间经过一段长度为20千米的区间测
（3）通过计算说明在此区间测速路段内，该辆汽车减速前是否超速.（此路段要求小型汽车行驶速度不得超过120千米/时）
例2 近年来，市民交通安全意识逐步增强，头盔需求量增大．某商店购进甲、乙两种头盔，已知购买甲种头盔20只，乙种头盔30只，共花费2 920元，甲种头盔的单价比乙种头盔的单价高11元．
（1）甲、乙两种头盔的单价分别是多少元？
（2）商店决定再次购进甲、乙两种头盔共40只，正好赶上厂家进行促销活动，促销方式如下：甲种头盔按单价的八折出售，乙种头盔每只降价6元出售．如果此次购买甲种头盔的数量不低于乙种头盔数量的一半，那么购买多少只甲种头盔，才能使此次购买头盔的总费用最少？最少费用是多少元？
命题点 一次函数的实际应用［8年3考］
A.正比例函数关系B.一次函数关系C.反比例函数关系D.二次函数关系
3.[2024南平质检] 北方某市对城市居民冬季的采暖收费标准如下表.（以户为单位）
根据表中所给的数据回答以下问题:
（3）已知某户这个冬季缴纳燃气费用8 970元,求该户用了多少立方米的燃气.
4.[2023龙岩质检] 世界文化遗产——福建土楼（龙岩·永定）是暑期热门的旅游目的地之一.某土楼纪念品专卖店销售甲、乙两种纪念品,每个甲种纪念品的进价比每个乙种纪念品的进价多 4元;用400元购进甲种纪念品和用240元购进乙种纪念品的数量相同.专卖店将每个甲种纪念品售价定为13元,每个乙种纪念品售价定为8元.
（1）每个甲种纪念品和每个乙种纪念品的进价分别是多少?
（2）根据市场调查,专卖店计划用不超过3 000元的资金购进甲、乙两种纪念品共400个,假设这400个纪念品能够全部卖出,求该专卖店获得最大销售利润的进货方案.
【新课标·综合与实践】【问题情境】如何分配工作，使公司支付的总工资最少？信息1：某包装公司承接到21 600个旅行包的订单，策划部准备将订单任务分配给甲、乙两个车间去完成．由于他们的设备与人数不同，甲车间每天生产的总数是乙车间每天生产总数的2倍，甲车间单独完成这项工作所需的时间比乙车间单独完成少18天．
【问题解决】任务1：确定工作效率.
（1）求甲、乙车间原来每天分别生产多少个旅行包.
任务2：探究抽走人数.
（2）甲、乙车间均被抽走了多少人？
任务3：拟订设计方案.