中考数学一轮复习讲练课件专题3.4 二次函数（含答案）

这是一份中考数学一轮复习讲练课件专题3.4 二次函数（含答案），共30页。PPT课件主要包含了二次函数图象与性质，求抛物线的解析式，二次函数与方程，yax2＋bx＋c，yax2+bx+c，上加下减，左加右减，-1-4，y-x2+2x+3，yx2-2x-3等内容，欢迎下载使用。
抛物线与a,b,c的关系
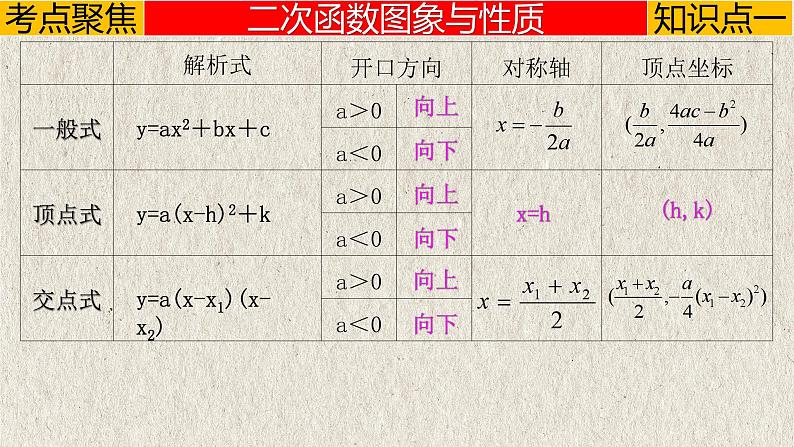
y=a(x-h)2＋k
y=a(x-x1)(x-x2)
【例1-1】(2015·T6)已知抛物线y=ax2+bx+c(a＞0)经过(-2,0),(2,3)两点,那么抛物线的对称轴( ) A.只能是x=-1 B.可能是y轴 C.在y轴右侧且在直线x=2的左侧 D.在y轴左侧
【变式】已知二次函数y=ax2+bx+c的图象开口向下,并经过(2,-3),(-2,0)两点,那么该函数图象的对称轴( ) A.有可能为y轴 B.有可能在y轴的右边且在直线x=2的左边 C.有可能是直线x=-2 D.有可能是直线x=2
【例1-2】对于二次函数y=ax2-2ax-3a+3的性质,下列说法中错误的是( ) A.抛物线的对称轴为直线x=1 B.抛物线一定经过两定点(-1,3)和(3,3) C.当a＜0时,抛物线与x轴一定有两个不同的交点 D.当a＞0时,抛物线与x轴一定有两个不同的交点(2)抛物线y=-x2+bx+c经过点(-2,3),则2c-4b-9的值是( ) A.5 B.-1 C.4 D.18
【例2-1】如图是抛物线y=ax2+bx+c(a≠0)的一部分,下列结论：①abc＜0；②b2-4ac＞0；③9a-3b+c＜0；④b-4a=0；⑤方程ax2+bx=0的两根为x1=0,x2=-4.其中正确的结论有( 　) A.①③④ B.②④⑤ C.①②⑤ D.②③⑤
【例2-2】在同一坐标系中,直线y=-mx+n2与抛物线y=x2+m的图象可能是( )
【变式】已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )
y=a(x-h)2+k
y=a(x-h+m)2+k
y=a(x-h-m)2+k
y=a(x-h)2+k+m
y=a(x-h)2+k-m
y=(x+1)2-4
y=-(x+1)2+4
y= (x-1)2-4
y=-(x-1)2+4
y=-(x+1)2-4
对称点(-x,-y)
代入y=x2+2x-3
【例3】(1)把抛物线y=-x2沿着x轴方向平移3个单位长度，那么平移后抛物线的解析式是_____________________.(2)将抛物线y=(x-1)2+2绕关于直线x=-1对称的新抛物线所对应的函数解析式是____________.
y=-(x+3)2或y=-(x-3)2
【例4】(1)已知二次函数y=x2-3x+m的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是(　 ) A.x1=1,x2=-1 B.x1=1,x2=2 C.x1=1,x2=0 D.x1=1,x2=3(2)如图,二次函数y=ax2+bx+c的图象则不等式的ax2+bx+c＜0解集是( 　) A.x＜-1 B.x＞3 C.-1＜x＜3 D.x＜-1或x＞3
1.抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( ) A.m＞1 B.m＞0 C.m＞-1 D.-1＜m＜02.已知a＞1,点(a-1,y1)(a,y2)(a+1,y3)都在函数y=x2+5的图象上,则( ) A.y1＜y2＜y3 B.y1＜y3＜y2 C.y3＜y2＜y1 D.y2＜y1＜y33.已知二次函数y=x2-2x-3,当0≤x≤3时,y的最大值和最小值分别是( ) A.0，-4 B.0，-3 C.-3，-4 D.0，04.如图,平面直角坐标系中,两条抛物线有相同的对称轴,则下列关系正确的是( ) A.m=n,k＞h B.m=n,k＜h C.m＞n,k=h D.m＜n,k=h
5.抛物线y=(x+3)(x-1)的对称轴是直线_______.6.若抛物线y=x2-8x+c的顶点在x轴上,则c=______.7.若抛物线y=x2-4x+k的顶点在x轴下方,则k的取值范围是______.8.若抛物线y=x2-2x+m-4与x轴有交点,则m的取值范围是____________.9.若抛物线y=x2+2x+c与坐标轴只有两个交点,则c的值为______.10.若函数y=mx2+2x+1的图像与x轴只有一个交点,则m=______.11.已知二次函数y=(a-2)x2+a2-2的最高点为(0,2)则a=______.12.抛物线y=(m+1)xm2-m+3,当x＞0时y随x的增大而增大,则m=_____.
1.下列关于抛物线的y=ax2-2ax-3a(a≠0)性质中不一定成立的是( )A.该图象的顶点为(1,-4a)； B.该图象与x轴的交点为(-1,0),(3,0)；C.当x＞1时,y随x的增大而增大；D.若该图象经过(-2,5),一定经过(4,5).2.抛物线y=(x-t)(x-t-2)(t为常数)与x轴交于A,B两点(点A在点B的左边),则下列说法不正确的是( ) A.点A,B的坐标分别是(t,0)(t+2,0) B.AB为定值 C.当y≥0时,t≤x≤t+2 D.y的最小值为-13.一元二次方程x2-mx+n=0无实根,抛物线y=x2-mx+n图象位于( ) A.x轴上方 B.第一二三象限 C.x轴下方 D.第二三四象限
4.已知在二次函数y=ax2-2x-3a的图象有三点A(x1,y1),B(x2,y2),C(0,-3),其中x1＜-1,0＜x2＜3,则y2-y1的值为( ) A.正数 B.负数 C.0 D.非负数5.如图为抛物线y=ax2+bx+c的图象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( ) A.a+b=-1 B.a-b=-1 C.b＜2a D.ac＜06.已知二次函数y=ax2+bx+c中,y与x的部分对应值如下表：根据表中信息,下列结论错误的是( ) A.其图象开口向下； B.其图象的对称轴为直线x=2 C.方程ax2+bx+c=0有一个根大于5； D.当x＜1时,y随x的增大而增大
用描点法画出函数的图象
7.抛物线y=(x-t)(x-t-2)(t为常数)与x轴交于A,B两点(点A在点B的左边),则下列说法不正确的是( ) A.点A,B的坐标分别是(t,0)(t+2,0) B.AB为定值 C.当y≥0时,t≤x≤t+2 D.y的最小值为-118.关于抛物线y=x2-(a+1)x+a-2,下列说法错误的是( ) A.开口向上 B.不论a为何值,都过定点(1,2) C.当a=2时,经过坐标原点O D.当a＞0时,对称轴在y轴的右侧9.已知抛物线y=ax2-4ax+m(a＞0)与直线y=3的一个交点为(-2,3),则关于x的一元二次方程ax2-4ax+m-3=0的两个实数根是____________.
10.抛物线y=ax2+c与坐标轴交于A(-2,0),B、C(0,-4)三点,S△ABC=___.11.抛物线y=ax2+bx+c与x轴交于点(-3,0),(1,0),则b∶a=______.12.已知点(m,n)在y=ax2+a(a≠0)的图象上,点(-m,n)____(填“在”或“不在”)y=ax2+a(a≠0)的图象上.13.若二次函数y=ax2+bx+c图象上部分点的坐标如下表,则该图象的顶点坐标为________.14.根据下列表格的值：判断方程ax2+bx+c=0(a≠0)一个解的范围是( ) A.3.1＜x＜3.2 B.3.2＜x＜3.3 C.3.3＜x＜3.4 D.3.4＜x＜3.5
15.抛物线y=ax2+bx+c的图象如图,则方程ax2+bx+c-8=0 的根的情况是___________________.16.若抛物线y=x2+bx+c的顶点在第一象限,则方程x2+bx+c=0 的根的情况是__________.17.函数y=ax2+2ax+m(a＜0)的图象过点(2,0),则使函数值y＜0成立的x的取值范围是_____________.18.已知抛物线y=ax2-4ax+m(且a＞0)与直线y=3的一个交点为(-2,3),则关于x的一元二次方程ax2-4ax+m-3=0的两个实数根是___________.
19.抛物线y=ax2+2ax+m(a＜0)过点(2,0),若y＜0,x的取值范围__________.20.若抛物线y=x2+2x+c与坐标轴只有两个交点,则c的值为______.21.如图,二次函数y=-x2+4与x轴交于A、B两点(点A在点B的左侧),等腰直角△ACD的直角顶点D在x轴上,AD=3.现将△ACD沿x轴的正方向平移,则当点C在函数图象上时,△ACD的平移距离为______.22.如图,抛物线y=ax2-4x+c经过坐标原点,与x轴交与点A(-4,0).若在抛物线上存在一点P,满足S△AOP=8,则点P的坐标___________________________.
23.已知二次函数y=ax2+bx+c中,y与x的部分对应值如下表：根据表中信息,下列结论错误的是( ) A.其图象开口向下. B.方程ax2+bx+c=0有一个根大于5. C.其图象的对称轴为直线x=2. D.当x＜1时,y随x的增大而增大.
24.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的表达式.
解:∵抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
又∵顶点在直线x=1上,且顶点到x轴的距离为5,
∴顶点为(1,5)或(1,-5)
(1)y=(x-1)2+5 (2)y=(x-1)2-5
(3)y=-(x-1)2+5 (4)y=-(x-1)2-5
25.已知关于x的二次函数y=mx2-(m+2)x+2(m≠0)．(1)求证：此抛物线与x轴总有两个交点；(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数, 求正整数m的值．
(1)证明：∵m≠0， ∴Δ=(m+2)2-4m×2 =m2+4m+4-8m=(m-2)2. ∵(m-2)2≥0， ∴Δ≥0，∴此抛物线与x轴总有两个交点；
(2)解:令y=0,则(x-1)(mx-2)=0， ∴x-1=0或mx-2=0， 解得 x1=1,x2=2/m. 当m为正整数1或2时,x2为整数,即抛物线与x轴总有两个交点,且它们的横坐标都是整数． ∴正整数m的值为1或2.