




所属成套资源:【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版)
- 专题03 分式与分式的基本性质(8大基础题+3大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版) 试卷 0 次下载
- 专题04 分式的运算(5大基础题+3大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版) 试卷 0 次下载
- 专题05 分式方程(7大基础题+5大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版) 试卷 0 次下载
- 专题06 三角形(8大基础题+5大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版) 试卷 0 次下载
- 专题08 三角形全等的五大基本模型(5大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版) 试卷 0 次下载
专题07 三角形全等的性质与判定(5大基础题+4大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版)
展开
这是一份专题07 三角形全等的性质与判定(5大基础题+4大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版),文件包含专题07三角形全等的性质与判定5大基础题+4大提升题原卷版docx、专题07三角形全等的性质与判定5大基础题+4大提升题解析版docx等2份试卷配套教学资源,其中试卷共73页, 欢迎下载使用。
全等三角形的性质
1.(23-24八年级上·湖南郴州·期末)如图,已知,若,则 .
【答案】/50度
【知识点】全等三角形的性质、三角形内角和定理的应用
【分析】本题考查了全等三角形的性质,三角形内角和定理,熟记性质并准确识图是解题的关键.根据全等三角形对应角相等可得,然后在中利用三角形内角和定理即可求出求出的度数.
【详解】解:∵,
∴,
∴.
故答案为:.
2.(23-24七年级下·江苏淮安·期末)如图,已知,若,则 .
【答案】/度
【知识点】三角形内角和定理的应用、全等三角形的性质
【分析】本题主要考查了全等三角形的性质,三角形内角和定理,先根据三角形内角和定理得到,再由全等三角形对应角相等得到.
【详解】解:∵,
∴,
∵,
∴,
故答案为:.
3.(23-24七年级下·河南南阳·期末)如图,,其中.则的周长为
【答案】
【知识点】全等三角形的性质
【分析】本题考查全等三角形的性质,掌握全等三角形的性质是解题的关键.根据全等三角形的性质得出,,进而可得出答案.
【详解】解:∵,,,,
∴,,
∴的周长为,
故答案为:15.
4.(23-24七年级下·山东青岛·期末)如图,已知,且点分别与点对应,,,则 .
【答案】6
【知识点】全等三角形的性质
【分析】本题考查了全等三角形的性质及线段的和差,熟练掌握全等三角形的性质定理是解题的关键.
先根据全等三角形的性质得出,再根据线段的和即可得出,然后将对应线段的长度代入计算即可得出答案.
【详解】
,
,,
故答案为:6.
5.(23-24七年级下·福建泉州·期末)如图,,,垂足分别为点、. 若,,,则 .
【答案】3
【知识点】全等三角形的性质
【分析】本题考查全等三角性的性质,属于基础题型,根据全等三角形的性质,得到,再根据线段的和差关系,求解即可.
【详解】解:∵,
∴,
∴;
故答案为:3.
添加一个条件使两三角形全等
1.(23-24八年级上·贵州遵义·期末)如图,线段是四边形的对角线,,请添加一个条件使得,添加的条件为 .
【答案】(答案不唯一)
【知识点】添加条件使三角形全等(全等三角形的判定综合)
【分析】本题考查了全等三角形的判定,解题的关键是掌握全等三角形的判定定理.根据全等三角形的判定定理,即可解答.
【详解】解:①当时,根据可判定;
②当时,根据可判定;
③当时,根据可判定;
故答案为:(或或).
2.(23-24七年级下·江西景德镇·期末)如图, D, E是边上的两点,, 现要直接用“”定理来证明, 请你再添加一个条件: .
【答案】
【知识点】用ASA(AAS)证明三角形全等(ASA或者AAS)、添加条件使三角形全等(全等三角形的判定综合)
【分析】在与中,已知,,即已知一角及角的一边对应相等,根据“”的判定方法,可以添加已知边的对角对应相等即可.本题考查了全等三角形的判定定理::两角及其中一个角的对边对应相等的两个三角形全等.判定两个三角形全等的一般方法有:、、、、.根据已知结合图形及判定方法选择条件是正确解答本题的关键.
【详解】解:可添加一个条件:,使.
理由:
在与中,
,
.
故答案为
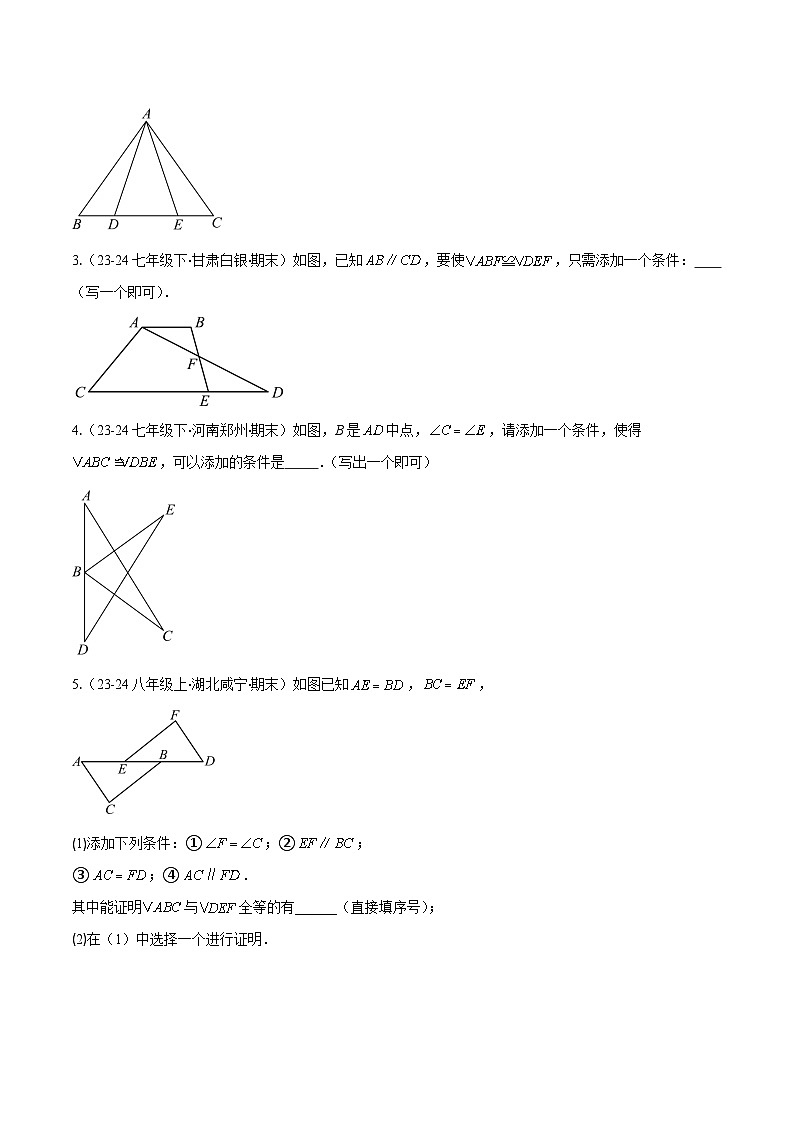
3.(23-24七年级下·甘肃白银·期末)如图,已知,要使,只需添加一个条件: (写一个即可).
【答案】(答案不唯一)
【知识点】添加条件使三角形全等(全等三角形的判定综合)
【分析】本题主要考查了全等三角形的判定,根据题意可知,推出,,则可添加条件,利用即可证明.
【详解】解:添加条件,理由如下:
∵,
∴,,
∴,
故答案为:(答案不唯一).
4.(23-24七年级下·河南郑州·期末)如图,B是中点,,请添加一个条件,使得,可以添加的条件是 .(写出一个即可)
【答案】(答案不唯一)
【知识点】添加条件使三角形全等(全等三角形的判定综合)
【分析】本题考查了全等三角形的判定.根据题意可知已有一组对应角和一组对应边相等,再确定一组对应角相等即可判定.
【详解】解:∵B是中点,
∴,
∵,
∴当时,依据可得,,
故答案为:(答案不唯一)
5.(23-24八年级上·湖北咸宁·期末)如图已知,,
(1)添加下列条件:①;②;
③;④.
其中能证明与全等的有______(直接填序号);
(2)在(1)中选择一个进行证明.
【答案】(1)②③
(2)见解析
【知识点】用SSS间接证明三角形全等(SSS)、添加条件使三角形全等(全等三角形的判定综合)
【分析】本题考查了添加条件使三角形全等及证明;
(1)根据全等三角形的判定定理即可解答;
(2)根据(1)所选取的条件,证明三角形全等即可.
【详解】(1)解:已知,,要使与全等可以添加的条件为或,能得到这些条件的有②③,
故答案为:②③;
(2)证明:选③,
∵,
∴,
即,
在与中,
,
∴.
利用尺规作图——三角形
1.(23-24八年级上·浙江·期末)已知和线段(如图).
(1)用直尺和圆规作(点在的上方),使,(做出图形,保留痕迹,不写作法).
(2)这样的三角形能作几个?
【答案】(1)见解析
(2)2
【知识点】尺规作一个角等于已知角、尺规作图——作三角形、作线段(尺规作图)
【分析】本题考查了作图—复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
(1)先作,再在上截取,然后以为圆心,为半径画弧交于和,则和即为所作;
(2)由作图即可得出答案.
【详解】(1)解:如图,和即为所作,
;
(2)解:由图可得:这样的三角形能作个.
2.(23-24七年级下·重庆·期末)如图,已知线段a,b和.
求作:,使得,,.(不写作法,不下结论,保留清晰的作图痕迹)
【答案】作图见解析
【知识点】尺规作图——作三角形
【分析】此题考查作图能力:作一角等于已知角,截取线段长度等于已知线段长,掌握简单的作图方法是解题的关键.先作,再在角的两边分别截取,,,则,从而可得答案.
【详解】解:如图,即为所求作的三角形;
3.(23-24七年级下·辽宁本溪·期末)尺规作图:
如图,线段和一副三角尺,其中.
求作:以线段为一条边作,使得.(要求:保留作图痕迹,不写作法)
【答案】见解析
【知识点】尺规作图——作三角形
【分析】本题考查尺规作三角形,根据尺规作角的方法作出,即可.掌握尺规作角的方法,是解题的关键.
【详解】因为
所以
如图所示,即为所求.
4.(23-24七年级下·广东佛山·期末)如题图,已知.
(1)请根据“”作,使,其中点D在右侧,且(要求:尺规作图,只保留作图痕迹,不要求写出作法):
(2)若,比的2倍小,求的度数.
【答案】(1)见解析
(2)
【知识点】解一元一次方程(一)——合并同类项与移项、三角形内角和定理的应用、尺规作图——作三角形、用SAS证明三角形全等(SAS)
【分析】(1)以点B为圆心,任意长度为半径作弧,分别交、于点E、F,再以点C为圆心,相同的半径作弧,交于点G,以点G为圆心,为半径作弧,交另一条弧于点O,连接并延长,再以点C为圆心,为半径作弧,交射线于点D,即可得,,连接,再利用“” ,即可求解;
(2)由题意得,根据三角形内角和定理可得,求得,从而可得,由(1)可得,,即可求解.
【详解】(1)解:以点C为顶点,为的一条边,作,,
在和中,
,
∴.
(2)解:∵比的2倍小,
∴,
∵,
∴,
∴,
∴,
∴,
由(1)可得,,
∴.
【点睛】本题考查作图−三角形、全等三角形的判定、三角形内角和定理及解一元一次方程,熟练掌握全等三角形的判定和作三角形方法是解题的关键.
5.(23-24七年级下·江苏淮安·期末)如图,已知线段m,n及.利用直尺和圆规作图,不写作法,保留作图痕迹;
(1)求作所有满足条件的(全等除外),使得;
(2)在(1)中所作图中,过点C向直线画垂线,与直线交于点H;并结合图形,直接写出三条线段、和的数量关系为 ;
【答案】(1)见解析
(2)或
【知识点】画出直线、射线、线段、尺规作图——作三角形、尺规作一个角等于已知角、作垂线(尺规作图)
【分析】本题主要考查了作一个角等于已知角,作一条线段等于已知线段的作法,都是基本作图,需要熟练掌握.
(1)第一种先做出,然后在边上截取得到点C,再以点为圆心,的长为半径作弧交射线于两点,连接即可得到和,则这两个三角行为符合题意的三角形;
(2)根据(1)中两种作图情况分别得出当即时,三条线段、和的数量关系:;当即时,三条线段、和的数量关系:.
【详解】(1)解:将原角按如下取点命名:
,
以点O为圆心,长为半径画弧,交两边于两点,再画射线,以长为半径画弧,交于点C ,再以C为圆心,的长为半径画弧,两弧交于点H ,连接,则,再以点为圆心,的长为半径作弧交射线于两点,连接即可得到和,则这两个三角行为符合题意的三角形,故两种作图如下:
;
(2)解:如题意画图如下,其中位置即为两种情况的位置,
当即时,三条线段、和的数量关系:,
当即时,三条线段、和的数量关系:,
故答案为:或.
三角形全等的判定与性质
1.(23-24八年级上·广东深圳·期末)如图,点D,E分别在和上,,点F是上一点,FE的延长线交延长线于点G.
(1)若,求的度数;
(2)若点E是的中点,与全等吗?请说明理由.
【答案】(1)
(2)不全等,理由见解析
【知识点】根据平行线判定与性质证明、三角形内角和定理的应用、全等三角形综合问题
【分析】本题考查平行线的性质,三角形内角和定理,利用平行线性质得出是解答本题的关键.
(1)根据平行线的性质得出,再根据三角形内角和定理即可得出结论;
(2)只有一边一角不能证两个三角形全等.
【详解】(1)解:∵,
∴,
又∵,
∴;
(2)解:不全等,理由如下:
∵点E是的中点,
∴,
∵,
只确定了这两个条件,无法证明全等.
2.(23-24八年级上·浙江宁波·期末)如图,已知,,,与交于点P,点C在上.
(1)求证:;
(2)若,.
①求的度数;
②求证:.
【答案】(1)见解析
(2)①;②见解析
【知识点】三角形的外角的定义及性质、全等三角形综合问题、等边对等角
【分析】本题考查了全等三角形的性质与判定,三角形外角的性质,等腰三角形性质,解题的关键是熟练掌握并运用相关知识.
(1)根据题意证明,由全等三角形的性质即可证明;
(2)①由三角形外角的性质求出,由全等三角形的性质得出,利用等腰三角形的性质求解,即可解题;
②利用“”证明,由全等三角形的性质即可得出结论.
【详解】(1)证明:,
,
即,
在和中,
,
,
;
(2)解:①,,
,
,
,
,
;
②证明:,
,
,
由①可知:,
在和中,
,
,
.
3.(23-24七年级下·黑龙江哈尔滨·期末)已知是的高,过作一直线,是直线上一点,是上一点,连接,.
(1)求证:;
(2)若,,,的面积是面积的3倍.求线段的长;
(3)若,,,请直接写出的面积与面积的比值(用含有的式子表示).
【答案】(1)见解析
(2)
(3)
【知识点】全等三角形综合问题
【分析】本题是三角形综合题,主要考查了全等三角形的性质与判定,三角形的面积等,掌握全等三角形的性质与判定是解题的关键.
(1)延长至点, 由得出得到 ;
(2)过点作交的延长线于点,证明 根据面积得到的长;
(3)设则 , 由(2)得, 得到根据 得出.
【详解】(1)证明:延长至点,
为的外角,
,
,
,
;
(2)过点作 交的延长线于点,
,
,
在和中,
,
∴,
∴,
在和中,
,
∴,
∴,
∵的面积是面积倍,
,
∵,
∴,
设, 则,
∴,
∴,
∴,
∴,解得x=1,
∴;
(3)设,, 则,,
由 (2) 得,
∴,
∴,
,
,
,
.
4.(23-24七年级下·陕西渭南·期末)如图,在四边形中,,过点作于点,,在上截取,连接,平分交的延长线于点,连接.
【问题解决】
(1)试说明:;
【问题探究】
(2)探索线段之间的数量关系并说明理由.
【答案】(1)证明见解析;(2),理由见解析
【知识点】全等三角形综合问题、三角形角平分线的定义
【分析】本题考查了全等三角形的判定与性质、角平分线的定义,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)先证明得出,再由角平分线的定义得出,即可得证;
(2)由得出,证明,得出,即可得出结论.
【详解】解:(1)∵,
∴,
∴,
在和中,
,
∴,
∴.
∵平分,
∴,
∴.
(2).理由如下:
∵,
∴,
在和中,
,
∴,
∴.
∵,
∴.
5.(22-23八年级上·四川南充·期末)都是等边三角形.
(1)如图,求证:;
(2)如图,点在内,为的中点,连,若,且.
①求证:;
②判断与的数量关系并证明.
【答案】(1)证明见解析
(2)①证明见解析;②,证明见解析
【知识点】等边三角形的判定和性质、含30度角的直角三角形、全等三角形综合问题
【分析】本题属于三角形综合题,考查了全等三角形的判定和性质,等边三角形的性质,直角三角形角的性质等知识,解题的关键是学会添加常用辅助线.
(1)证明,可得结论;
(2)①如图中,延长到,使得,连接.证明,推出,,,再证明,可得结论;
②根据得到,设,根据列出方程,求出,可得结论.
【详解】(1)证明:如图中,
∵都是等边三角形
∴,,,
∴,
在和中,
∴,
∴;
(2)①证明:如图中,延长到,使得,连接,
∵,
∴,
在和中,
∴,
∴,,
同法可证,
∴,
∵,
∴,
∵,
∴,
∵,
∴.
②结论:.
证明:∵,
∴,
设,则,
∵,
∴,
∴,
∴,
∵,
∴,
∵,,
∴.
用HL证明两直角三角形全等
1.(23-24八年级上·广东肇庆·期末)如图,中,为上一点,为延长线上一点,且,过点作于点,过点作交的延长线于点,且,连交边于.求证:
(1);
(2).
【答案】(1)见解析
(2)见解析
【知识点】全等三角形综合问题、全等的性质和HL综合(HL)
【分析】本题考查了三角形全等的判定与性质.熟练掌握三角形全等的判定与性质是解题的关键.
(1)由“”可证;
(2)先由(1)可知,证,从而由三角形全等的性质可得,然后由线段的和差即可得证.
【详解】(1)证明:∵,,
∴在与中,
,
;
(2)证明:由(1)知,
,
∵,,
,
在与中,
,
,
,
,
.
2.(22-23八年级上·北京朝阳·期末)如图,于点E,于点F,.
(1)求证:;
(2)求证:.
【答案】(1)见解析
(2)见解析
【知识点】同位角相等两直线平行、全等的性质和HL综合(HL)
【分析】本题考查全等三角形的判定与性质,平行线的判定,正确理解题意是解题的关键.
(1)先证明,再根据,即可证明;
(2)根据全等三角形的性质得出,根据平行线的判定即可得出结论.
【详解】(1)证明:∵于点于点,
,
,
,
在和中,
,
;
(2)证明:,
,
.
3.(23-24七年级下·四川甘孜·期末)如图,已知,,,,与交于点O.
(1)求证:.
(2)求.
【答案】(1)见解析
(2)
【知识点】三角形的外角的定义及性质、全等的性质和HL综合(HL)
【分析】本题考查全等三角形的性质和判定,三角形外角的性质,
(1)根据证明两个三角形全等即可;
(2)根据三角形全等的性质和三角形外角的性质可得结论;
解题的关键是掌握三角形全等的判定.
【详解】(1)证明:∵,
∴,即,
∵,
在和中,
,
∴;
(2)解:∵,,
∴,
由(1)知:,
∴,
∴,
∴,
∴的度数为.
4.(23-24八年级下·山东青岛·期末)如图,等腰中,是腰上的高,在底边上截取,过点E作交于F.
(1)求证:
(2)若,求的度数.
【答案】(1)见解析
(2)
【知识点】直角三角形的两个锐角互余、三角形的外角的定义及性质、全等三角形的性质、全等的性质和HL综合(HL)
【分析】本题主要考查了全等三角形的性质和判定,等腰三角形的性质,三角形的外角的性质,
(1)直接利用证明,根据全等三角形的性质可得结论;
(2)先根据直角三角形的性质求出,再根据全等三角形的性质求出,然后根据等边对等角得,进而求出,可得答案.
【详解】(1)证明:∵是腰上的高,,
∴.
又∵,,
∴,
∴;
(2)∵,,
∴.
∵,
∴,
∴.
∵是等腰三角形,
∴.
∵是的外角,
∴,
∴.
5.(23-24七年级下·四川成都·期末)如图,与中,,,线段与线段在一条直线上,且,连接,,,与相交于点.
(1)与全等吗?为什么?
(2)试说明点是线段的中点.
【答案】(1)全等,理由见解析
(2)说明见解析
【知识点】全等三角形综合问题、全等的性质和SAS综合(SAS)、全等的性质和ASA(AAS)综合(ASA或者AAS)、全等的性质和HL综合(HL)
【分析】本题考查了全等三角形的判定与性质,中点定义等知识,熟记全等三角形的判定定理与性质定理是解题的关键.
(1)利用证明,根据全等三角形的性质得出,,再利用即可证明;
(2)利用证明,根据全等三角形的性质及线段中点定义即可得解.
【详解】(1)解:,
理由如下:
,
,即,
在与中,
,
,
,,
在和中
,
;
(2)解:由(1)知,,
与相交于点,
,
在和中,
,
,
,
点是线段的中点.
利用三角形全等求时间或线段长的多解问题
1.(23-24七年级下·江苏苏州·期末)如图,在四边形中,,.动点P以的速度从点A出发沿边向点D匀速移动,动点Q以的速度从点B出发沿边向点C匀速移动,动点M从点B出发沿对角线向点D匀速移动,三点同时出发.连接,当动点M的速度为 时,存在某个时刻,使得以P、D、M为顶点的三角形与全等.
【答案】或
【知识点】几何问题(二元一次方程组的应用)、全等三角形的性质
【分析】本题主要考查了全等三角形的性质,平行线的性质,解二元一次方程组,设运动的时间为,动点M的速度为,则,进而得到,再分当时,当时,两种情况根据全等三角形对应边相等建立方程组求解即可.
【详解】解:设运动的时间为,动点M的速度为,
由题意得,,
∴.
∵,
∴.
当时,则,
∴,
解得,
∴,
解得.
当时,则,
∴,
解得,
∴,
解得.
综上所述,动点M的速度为或,
故答案为:或.
2.(23-24八年级上·河南商丘·期末)如图,,E、F分别为线段和射线上的一点,若点E从点B出发向点A运动,同时点F从点B出发沿射线运动,二者速度之比为2:3,当点E运动到点A时,两点同时停止运动.在射线上取一点G,使与全等,则的长为 .
【答案】8或15
【知识点】全等三角形的性质
【分析】本题主要考查了全等三角形的性质,掌握分类讨论思想是解题的关键.
设,则,使与全等;然后分和两种情况解答即可.
【详解】解:设,则,使与全等
①当时,
∵,
∴,解得:,
∴.
②当时,
∵,
∴,解得:,
∴,
综上所述,或.
故答案为:8或15.
3.(23-24七年级下·河南驻马店·期末)如图,在长方形中 ,,,,,延长至点E,使,连接.动 点P 从 点A 出发,以每秒2个单位长度的速度沿运动,回到点A 停止运动,运动时间为:t秒,当t 的值为 时,和全等.
【答案】或 10
【知识点】全等三角形的性质
【分析】此题考查了全等三角形的性质和判定,根据题意分两种情况:和,然后根据全等三角形的性质求解即可.
【详解】解:如图所示,当时,
∴
∵在长方形中,,,
∴,
∴
∵点P的运动时间为每秒2个单位
∴(秒);
如图所示,当时,
∴,
∴,
∴(秒)
综上所述,当t的值为或10秒时,与全等.
故答案为:3.5或10.
4.(23-24八年级上·河南焦作·期末)如图,直线与x轴和y轴分别交于A、B两点,射线于点A.若点C是射线上的一个动点,点D是x轴上的一个动点,且以C、D、A为顶点的三角形与全等,则点D的坐标为 .
【答案】或
【知识点】一次函数图象与坐标轴的交点问题、一次函数与几何综合、全等三角形的性质
【分析】本题考查一次函数与几何的综合应用,先求出两点的坐标,进而求出的长,分或两种情况进行讨论求解即可.利用数形结合和分类讨论的思想,进行求解,是解题的关键.
【详解】解:当时,,
∴点B的坐标为0,2,
∴,
当时,,
解得:,
∴点A的坐标为,
∴,
∴,
∵,
∴,
如图所示,
∵,,
∴,
当以C、D、A为顶点的三角形与全等时,共有或两种情况,
当时,,
∴点D的坐标为,即;
当时,,
∴点D的坐标为.
综上所述,点D的坐标为或.
故答案为:或.
5.(23-24八年级上·湖北鄂州·期末)如图,中,,,.点从点出发沿路径向终点运动,终点为点;点从点出发沿路径向终点运动,终点为点.点和分别以每秒1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过和作于、作于,当点运动 秒时,以、、为顶点的三角形和以、、为顶点的三角形全等.
【答案】2或7或24
【知识点】全等三角形的性质、几何问题(一元一次方程的应用)
【分析】本题主要考查对全等三角形的性质,解一元一次方程等知识点的理解和掌握,能根据题意得出方程是解此题的关键.根据题意分为五种情况,根据全等三角形的性质得出,代入得出关于t的方程,解方程即可.
【详解】解:设点运动秒时,以、、为顶点的三角形和以、、为顶点的三角形全等,分为五种情况:
①如图1,P在上,Q在上,则,,
,,
,
,
,,
,
,
,
即,
;
②如图2,P在上,Q在上,则,,
由①知:,
,
;
因为此时,所以此种情况不符合题意;
③当P、Q都在上时,如图3,
,
解得:;
④当Q到A点停止,P在上时,如图4,,时,解得.
,符合题意;
⑤因为P的速度是每秒1,Q的速度是每秒3, P和Q都在上的情况不存在;
综上,点P运动2或7或24秒时,以P、E、C为顶点的三角形上以Q、F、C为顶点的三角形全等.
故答案为:2或7或24.
与全等三角形有关的多结论问题
1.(23-24七年级下·黑龙江哈尔滨·期末)如图,在中,,为边上一点,,点在的延长线上,平分,且.连接交于,为边上一点,满足,连接交于.以下结论:①;②;③.正确的有( )
A.0个B.1个C.2个D.3个
【答案】D
【知识点】全等的性质和SAS综合(SAS)、三角形内角和定理的应用
【分析】本题考查了三角形全等的判定与性质,三角形内角和定理等知识,熟练掌握三角形全等的判定与性质是解题关键.
先根据邻补角的定义可得,再根据角平分线的定义可得,然后利用定理证明出,进而判断①;利用证明出进而可判断②;得到,然后利用三角形内角和定理求解即可.
【详解】,
,
平分,
,
,
在和中,
,
,故①正确;
∵,,
∴,故②正确;
∴
又∵
∴,故③正确.
综上所述,正确的有3个.
故选:D.
2.(23-24七年级下·陕西咸阳·期末)如图,在与中,,,,分别交,于点,,交于点,则下列结论:①;②;③;④,其中正确的有( )
A.4个B.3个C.2个D.1个
【答案】B
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)
【分析】本题考查全等三角形的判定和性质,利用可证明,即可得,,,进而可判断①②正确,再利用可证明,即可判断④正确,再证明,,可知,根据题目条件,不能判断出与的大小关系,因此不能判断与是否相等,进而可知③不正确,理解并掌握全等三角形的判定及性质是解题的关键.
【详解】解:,,,
,
,,,故②正确,
,
即,故①正确,
,,,
,故④正确,
,,,
,
,
又,
,即,
,,,
,
,
根据题目条件,不能判断出与的大小关系,因此不能判断与是否相等,故③错误,
综上,正确的有①②④;
答案:B.
3.(23-24八年级上·云南红河·期末)如图所示,,,,点F是的中点.①;②;③;④;⑤.以上结论,正确的是( )
A.①③④⑤B.②③④⑤C.①②③④D.①②③④⑤
【答案】C
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、两直线平行内错角相等
【分析】此题考查了全等三角形的性质和判定,三角形中线的性质,解题的关键是掌握以上知识点.
根据题意证明出,进而判断①;然后根据全等三角形的性质可判断②③;然后根据三角形中线的性质可判定④;然后根据直角三角形斜边中线的性质可判断⑤.
【详解】解:∵
∴
又∵,,
∴,故①正确;
∴
∴,故②正确;
∵
∴,
∴,即
又∵
∴
∴
∴,故③正确;
∵点F是的中点
∴,故④正确;
∵
∴,故⑤错误.
综上所述,正确的是①②③④.
故选:C.
4.(23-24八年级上·湖北黄石·期末)如图,在中,,,、是斜边上两点,且,过点作,垂足是,过点作,垂足是交于点,连接,下列结论:≌;;若,,则;其中正确的是 .
【答案】
【知识点】全等三角形综合问题
【分析】本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,只要证明,即可解决问题.
【详解】解:∵,
∴,
∵,
∴,
∵,
∴,
∴,
在和中,
,
∴,故①正确
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,故②正确,
∵若.
∴,
∴,
∵,
∴,故③正确,
∵,,
∴,故④错误,
故答案为:①②③.
全等三角形中的动点综合问题
1.(23-24七年级下·全国·期末)如图,在中,,D为射线上一动点(不与点B、C重合),在的右侧作,使得,连接.
(1)当点D在线段上时,求证:;
(2)若点D运动到线段上某一点时,恰好有,问:线段与线段有什么位置关系并说明理由;
(3)在点D的运动过程中,当垂直于的某边时,则 (用含α的代数式表示).
【答案】(1)见解析;
(2),理由见解析;
(3)或
【知识点】等边三角形的判定和性质、全等的性质和SAS综合(SAS)、三角形内角和定理的应用
【分析】(1)由得,利用即可得出结论;
(2)由(1)知,根据全等三角形的性质得,,则,可得为等边三角形,则,可得,得出,根据平行线的判定可得;
(3)分两种情形:当时,当时,利用三角形内角和定理以及等腰三角形的性质求解即可.
本题是三角形综合题,考查了等腰三角形的性质、全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是准确寻找全等三角形解决问题,学会用分类讨论的首先思考问题,属于中考压轴题.
【详解】(1)证明:如图,
,
,
,
在和中,
,
;
(2)解:,理由如下:
由(1)知,
,,
,
,
,
,
为等边三角形,
,
,
,
;
(3)解:如图,当时,
,,
,
,
,,
,
,
,
,
,
;
如图,当时,
,
,
由(1)知,,
,
,
,
,,
,
,
.
综上所述,当垂直于的某边时,则或.
故答案为:或.
2.(23-24八年级上·贵州遵义·期末)在中,,点E为上一动点,过点A作于D,连接.
(1)【观察发现】
如图①,与的数量关系是 ;
(2)【尝试探究】
点E在运动过程中,的大小是否改变,若改变,请说明理由,若不变,求的度数;
(3)【深入思考】
如图②,若E为中点,探索与的数量关系.
【答案】(1)
(2)的大小不变,
(3)
【知识点】同(等)角的余(补)角相等的应用、全等三角形综合问题、旋转模型(全等三角形的辅助线问题)
【分析】此题考查等腰直角三角形的判定与性质、全等三角形的判定与性质等知识.
(1)由,得,而,所以,于是得到问题的答案;
(2)作交于点F,则,而,即可证明,得,则,所以的大小不改变,;
(3)作交于点G,作于点H,可证明,得,由,得,则,由,得,则,所以,即可推导出.
【详解】(1)∵
∴,
∴,
∵,
∴,
故答案为:.
(2)的大小不改变,
如图①,作交于点F,则,
∴,
由(1)得,
∵
∴,
∴,
∴,
∴的大小不改变,.
(3),
理由:如图②,作交于点G,作于点H,则
∴,
∵E为中点,
∴,
∵,
∴,
∴,
由(2)得,
∴,
∴,
∵,
∴,
∴,
∴,
∴.
3.(23-24八年级上·湖南株洲·期末)如图,等腰中,,,点为射线上一动点,连接,作且.
(1)如图1,过F点作交于G点,求证:;
(2)如图2,连接交于点,若,求证:点为中点;
(3)如图3,当点在的延长线上时,连接与的延长线交于点,若,则 .
【答案】(1)见解析
(2)见解析
(3)
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、全等三角形综合问题
【分析】本题考查了全等三角形的判定以及性质.
(1)易证,即可证明,即可解题;
(2)过点作交于点,根据(1)中结论可得,即可证明,可得,根据可证,根据,,即可解题;
(3)过作的延长线交于点,易证,由(1)(2)可知,,可得,,即可求得的值,即可解题.
【详解】(1)证明:,,
,
在和中,
,
;
(2)证明:过点作交于点,
,
,
在和中,
,
,
,
,
,
,
,
,
点为中点;
(3)解:过作的延长线交于点,如图,
,,,
,
由(1)(2)知:,,
,,
,
,
,
.
故答案为.
4.(23-24七年级下·广东深圳·期末)如图,在中,为锐角,点D为直线上一动点,以为直角边且在的右侧作等腰直角三角形,,.
(1)如果,.
①当点D在线段上时,如图1,线段、的位置关系为________,数量关系为________;
②当点D在线段的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果,,点D在线段上运动.
探究:当多少度时,?请说明理由.
【答案】(1)①,;②仍然成立,理由见解析
(2)当时,,理由见解析
【知识点】全等的性质和SAS综合(SAS)、垂线的定义理解
【分析】本题为三角形综合题,主要考查了全等三角形的判定与性质及等腰直角三角形的性质,解决问题的关键是证明全等三角形,根据全等三角形的对应边相等,对应角相等进行求解.
(1)①根据,,,运用“”证明,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段、之间的关系;
②先根据“”证明,再根据全等三角形性质得出对应边相等,对应角相等,即可得到(1)中的结论仍然成立.
(2)过点A作交的延长线于点G,证明,根据对应角相等即可得出结论.
【详解】(1)解:①与位置关系是,数量关系是.
理由:
,,
.
又,,
,
且.
,
,即.
故答案为:,;
②都成立
,
,
在与中,
,
,,
,即.
(2)解:当时,.
理由:过点A作交的延长线于点G,则,
∵,
∴,
∴
∴,
在与中,
,
∴,
∴,
∴,即.
三角形全等之新定义型综合问题
1.(23-24七年级下·陕西宝鸡·期末)【阅读理解】
定义:在同一平面内,点A,B分别在射线,上,过点A垂直的直线与过点B垂直的直线交于点Q,则我们把称为的“边垂角”.
【迁移运用】
(1)如图1,,分别是的两条高,两条高交于点F,根据定义,我们知道是的“边垂角”或是的“边垂角”,的“边垂角”是______;
(2)若是的“边垂角”,则与的数量关系是______;
(3)若是的“边垂角”,且.如图2,交于点E,点C关于直线对称点为点F,连接,,且,求证:.
【答案】(1)
(2)或
(3)见解析
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、全等的性质和SAS综合(SAS)、三角形内角和定理的应用
【分析】本题主要考查了全等三角形的性质与判定,四边形内角和定理:
(1)根据“边垂角”的定义即可得到答案;
(2)分两种情况画出图形,根据四边形的内角和定理以及等角的余角相等即可得出结论;
(3)延长交于点,先证明,再证明,依据题意得出,即可得到结论.
【详解】(1)解:根据“边垂角”的定义,的“边垂角”是;
(2)解:若是的“边垂角”,分两种情况
①如图,是的“边垂角”,
,
,
,
,
②如图,
是的“边垂角”,
,
,
,
,
综上所述,与的数量关系是或;
(3)解:延长交于点,
是的“边垂角”,
∴,
,
,
,
,
,
,
,
,
,
,
,
,
点关于直线对称点为点,
,
,
;
2.(23-24七年级下·江苏南京·期末)定义:只有一组对角相等的四边形叫做等角四边形.如:在四边形中,若,且,则称四边形为等角四边形,记作等角四边形.
【初步认识】
(1)如图,四边形是等角四边形,,,则_____;
【继续探索】
(2)如图,四边形是等角四边形,平分,平分,求证:;
(1)如图,已知,点分别在边上.在的内部求作一点,使四边形是等角四边形,且.
(要求:用无刻度直尺和圆规作图,保留作图痕迹,写出必要的文字说明.)
【答案】(1)135;(2)证明见解析;(3)见解析
【知识点】尺规作一个角等于已知角、同位角相等两直线平行、角平分线的有关计算
【分析】(1)由题意得出,再由计算即可得出答案;
(2)设,由角平分线的定义得出,,求出,在计算出,得出,即可得证;
(3)根据等角四边形的定义作图即可.
【详解】(1)解:∵四边形是等角四边形,,,
∴,
∴;
(2)证明:∵四边形是等角四边形,
∴,
设,
∵在四边形中,,
∴,
∵平分,平分,
∴,,
∴,
∵在中,,
∴,
∴,
∴;
(3)解:如图,连接,作,作射线,作,,、交于点,点即为所求,
,
∵,,,
∴,
∵,,
∴,
∴四边形是等角四边形,
∴点即为所求.
【点睛】本题考查了角平分线的定义、作图—设计与应用作图、三角形内角和定理、平行线的判定等知识点,熟练掌握以上知识点并灵活运用是解此题的关键.
3.(23-24七年级下·辽宁本溪·期末)新定义:如果两个三角形不全等但面积相等,那么这两个三角形叫做积等三角形.
【初步尝试】
(1)如图1,在中,,P为边上一点,若与是积等三角形,求的长;
【理解运用】
(2)如图2,与为积等三角形,若,且线段AD的长度为正整数,求AD的长.
【综合应用】
(3)如图3,在中,过点C作,点是射线上一点,以为边作,连接.请判断与是否为积等三角形,并说明理由.
【答案】(1)2;(2)2;(3)是积等三角形,证明见解析
【知识点】全等的性质和SAS综合(SAS)、根据三角形中线求面积、确定第三边的取值范围
【分析】本题考查了等腰直角三角形的性质,三角形的中线的性质,三角形的三边关系等知识,解题的关键是正确寻找全等三角形解决问题.
(1)利用三角形的中线的性质即可解决问题;
(2)证明,推出,利用三角形的三边关系即可解决问题;
(3)过过点作于点,先证明 则,然后再依据积等三角形的定义进行证明即可.
【详解】(1)解:过点作于,
与是积等三角形,
,
,
,
;
(2)解:如图2,延长至,使,连接,
与为积等三角形,
在和中,
,
在中
为正整数,
;
(3)是积等三角形
证明:如图3,过点作于点,
在和中,
,
与为积等三角形.
4.(23-24八年级下·重庆江津·期末)定义:如图(1),若分别以的三边,,为边向三角形外侧作正方形,和,则称这三个正方形为的外展三叶正方形,其中任意两个正方形为的外展双叶正方形.
(1)作的外展双叶正方形和,记,的面积分别为和;
①如图(2),当时,求证:;
②如图(3),当时,与是否仍然相等,请说明理由.
(2)已知中,,,作其外展三叶正方形,记,,的面积和S,请利用图(1)探究:当的度数发生变化时,的值是否发生变化?若不变,求出的值;若变化,求出的最大值.
【答案】(1)①见解析;②相等,理由见解析
(2)变化,最大值为18
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、全等的性质和SAS综合(SAS)、三角形的分类
【分析】(1)①由正方形的性质可以得出,,,即可得出而得出结论;
②如图3,过点作于点,过点作交的延长线于点,通过证明就有而得出结论;
(2)根据(1)可以得出,要使最大,就要使最大,当时最大,即可求出结论.
【详解】(1)解:①证明:正方形和正方形,
,,,
,
,
.
在和中,
,
.
,
.
②.
理由如下:
如图3,过点作于点,过点作交的延长线于点.
.
四边形,四边形均为正方形,
,,
,.
.
在和中,
,
,
.
,
,,
;
(2)的值发生变化;的最大值为18;理由如下:
由(1)得,是面积的三倍,
要使最大,只需的面积最大,
当是直角三角形,即时,有最大值.
此时,.
【点睛】本题考查了正方形的性质、全等三角形的判定及性质、直角三角形的性质、三角形的面积公式;本题难度较大,综合性强,证明三角形全等是解决问题的关键.
相关试卷
这是一份专题05 分式方程(7大基础题+5大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版),文件包含专题05分式方程7大基础题+5大提升题原卷版docx、专题05分式方程7大基础题+5大提升题解析版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
这是一份专题04 分式的运算(5大基础题+3大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版),文件包含专题04分式的运算5大基础题+3大提升题原卷版docx、专题04分式的运算5大基础题+3大提升题解析版docx等2份试卷配套教学资源,其中试卷共48页, 欢迎下载使用。
这是一份专题03 分式与分式的基本性质(8大基础题+3大提升题)-【好题汇编】备战2024-2025学年八年级数学上学期期末真题分类汇编(人教版),文件包含专题03分式与分式的基本性质8大基础题+3大提升题原卷版docx、专题03分式与分式的基本性质8大基础题+3大提升题解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。









