辽宁省锦州市第四中学教育集团2024-2025学年上学期八年级期中考试数学试卷（原卷版）-A4

这是一份辽宁省锦州市第四中学教育集团2024-2025学年上学期八年级期中考试数学试卷（原卷版）-A4，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 下列各数中，是无理数的是（ ）
A. 3.1415B. C. D.
2. 下列等式正确的是（ ）
A. B. C. D.
3. 下列函数中，正比例函数（ ）
A. B. C. D.
4. 在平面直角坐标系中，点关于轴对称的点的坐标为（ ）
A. B. C. D.
5. 若点P是第三象限内的点，且点P到x轴的距离是4，到y轴的距离是3，则点P的坐标是（ ）
A. （﹣4，-3）B. （4，﹣3）C. （﹣3，-4）D. （3，﹣4）
6. 由下列条件不能判定为直角三角形的是（ ）
A B. ，，
C. D.
7. 若点都在一次函数图象上，则与大小关系是（ ）
A. B. C. D. 无法比较大小
8. 如图，长方形中，在数轴上，若以点为圆心，的长为半径作弧交数轴于点，则点表示的数为( )
A. B. C. 2D.
9. 在同一平面直角坐标系中，函数和的图象可能是（ ）
A. B. C. D.
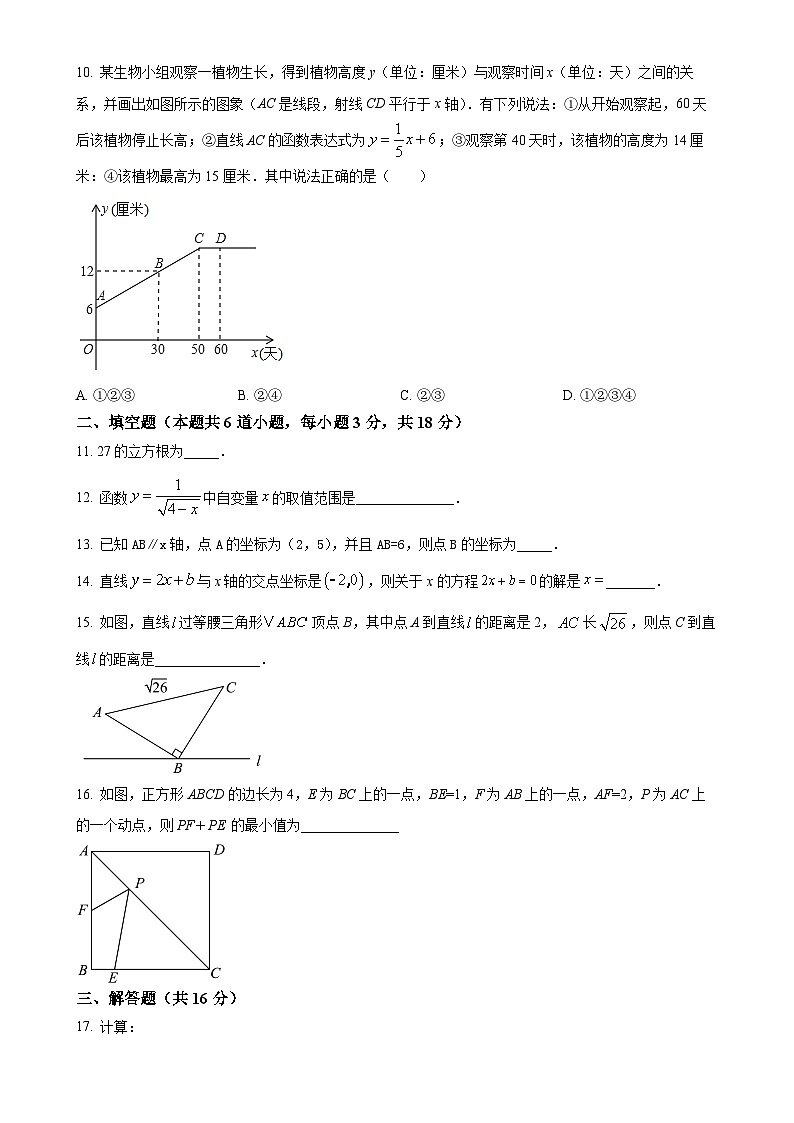
10. 某生物小组观察一植物生长，得到植物高度y（单位：厘米）与观察时间x（单位：天）之间的关系，并画出如图所示的图象（AC是线段，射线CD平行于x轴）．有下列说法：①从开始观察起，60天后该植物停止长高；②直线AC的函数表达式为；③观察第40天时，该植物的高度为14厘米：④该植物最高为15厘米．其中说法正确的是（ ）
A. ①②③B. ②④C. ②③D. ①②③④
二、填空题（本题共6道小题，每小题3分，共18分）
11. 27的立方根为_____．
12. 函数中自变量的取值范围是______________．
13. 已知AB∥x轴，点A的坐标为（2，5），并且AB=6，则点B的坐标为_____．
14. 直线与x轴的交点坐标是，则关于x的方程的解是_______．
15. 如图，直线过等腰三角形顶点B，其中点A到直线的距离是2，长，则点C到直线的距离是_______________．
16. 如图，正方形ABCD的边长为4，E为BC上的一点，BE=1，F为AB上的一点，AF=2，P为AC上的一个动点，则PF＋PE 的最小值为______________
三、解答题（共16分）
17. 计算：
（1）
（2）
（3）
（4）
四、解答题（共两道题，18题6分，19题8分．共14分）
18. 如图所示，在平面直角坐标系中，已知、、．
（1）在平面直角坐标系中画出，则的面积是 ；
（2）若点D与点C关于y轴对称，则点D的坐标为 ；
（3）已知P为x轴正半轴上一点，若的面积为1，求点P的坐标．
19. 数学兴趣小组利用所学数学知识来解决实际问题，实践报告如下：
小组成员测量了相关数据，并画出了如图所示的示意图，测得水平距离的长为15米，根据手中剩余线的长度计算出风筝线的长为17米，牵线放风筝的手到地面的距离为1.5米．
（1）求的长．
（2）如果想要风筝沿方向再上升12米，且长度不变，则他应该再放出多少米线．
五、解答题（共两道题，20题6分，21题8分，共14分．）
20. 数学精英小组利用平面直角坐标系在研究直线上点的坐标规律时，发现直线上的任意三点，，（），满足，经小组查阅资料，再经请教老师验证，以上结论是成立的，即直线上任意两点的坐标，，（），都有．例如：，为直线上两点，则．
（1）已知直线经过，两点，请直接写出______．
（2）如图，直线于点，直线，分别交轴于，两点，，，三点坐标如图所示．请用上述方法求出的值．
21. 某校计划购买一批篆刻石料，已知两个商家的标价相同，但甲商家提出:若购买一张会员卡，则每块篆刻石料打七折；乙商家提出：每块篆刻石料按标价的九折出售．设购买篆刻石料的数量为块，则甲商家所需费用，乙商家所需费用，则函数图象如图所示．
（1）甲商家一张会员卡的价格为______________元，每块篆刻石料的标价为____________元，____________
（2）两个函数图象的交点的坐标为____________．
（3）若该校准备购买40块篆刻石料，则选择哪家商家比较合算？请说明理由．
（4）若本次够买篆刻石料的经费有元，则选择哪个商家购买的篆刻石料数量会更多？请说明理由．
六、解答题(共两道题，22题8分，23题10分，共18分)
22. 如图所示，平面直角坐标系中，直线AB交x轴于点B（﹣3，0），交y轴于点A（0，1），直线x=﹣1交AB于点D，P是直线x=﹣1上一动点，且在点D上方，设P（﹣1，n）．
（1）求直线AB的解析式；
（2）求△ABP的面积（用含n的代数式表示）；
（3）点C是y轴上一点，当S△ABP=2时，△BPC是等腰三角形，
①满足条件的点C的个数是________个（直接写出结果）；
②当BP为等腰三角形的底边时，求点C的坐标．
23. 在等腰直角．
（1）如图1，D，E等腰直角斜边上两动点，且，将绕点A逆时针旋转得到，连接．
①求证：；
②当时，求的长．
（2）如图2，是等腰直角斜边所在直线上一动点，连接，以为直角顶点作等腰直角，当时，则________________．