黑龙江省哈尔滨德强学校2024-2025学年八年级上学期9月份学情检测数学试卷（原卷版）-A4

这是一份黑龙江省哈尔滨德强学校2024-2025学年八年级上学期9月份学情检测数学试卷（原卷版）-A4，共6页。试卷主要包含了选择题等内容，欢迎下载使用。
一、选择题（每小题3分，共计27分）
1. 下列计算中，结果正确的是（ ）
A. B. C. D.
2. 点关于轴对称点的坐标是（ ）
A. B. C. D.
3. 等腰三角形的两边长分别是2和7，则它的第三边长是（ ）
A 2B. 7C. 9D. 11
4. 如图，DE是△ABC中AC边的垂直平分线，若BC=8，AB=10，则△EBC的周长是( )
A 13B. 16C. 18D. 20
5. 如图，△ABC是等边三角形，DE//BC，若AB＝7，BD＝3，则△ADE的周长为（ ）
A. 4B. 9C. 12D. 21
6. 如图，在中，交于点，则的长为（ ）
A. 18B. 10C. 11D. 12
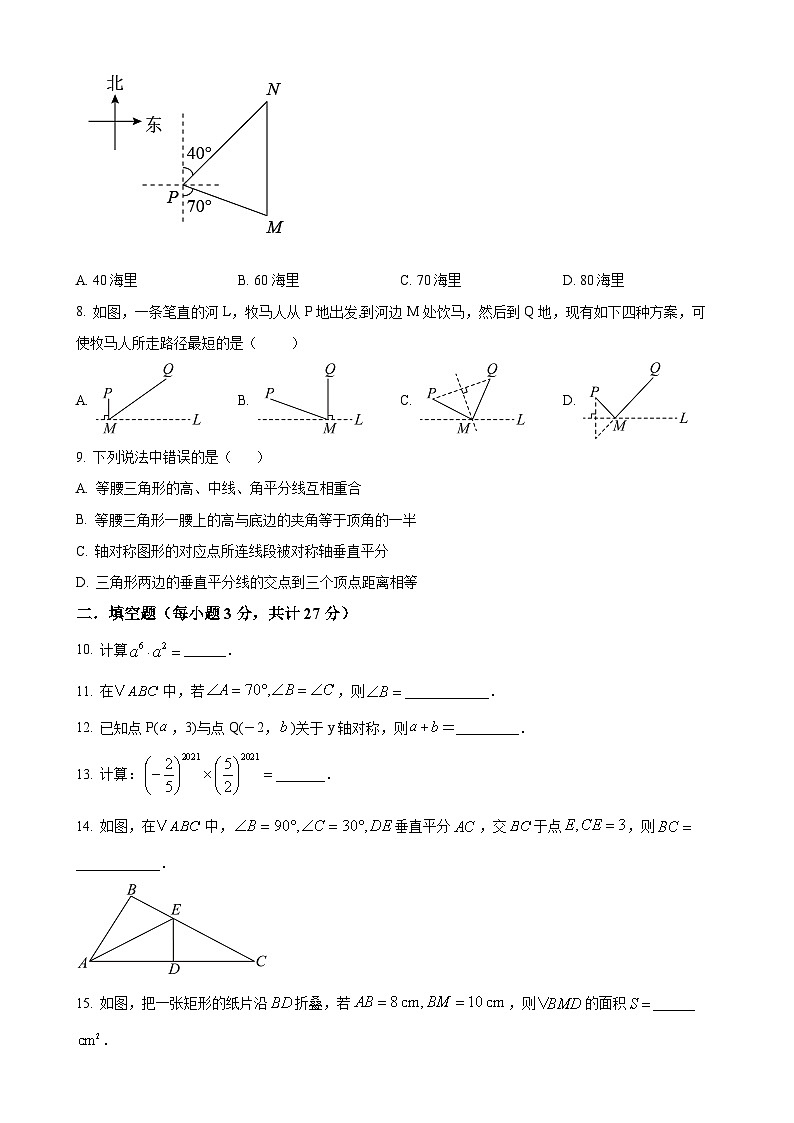
7. 如图，一艘海轮位于灯塔P的南偏东70°方向的M处， 它以每小时40海里的速度向正北方向航行，2小时后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P的距离为
A. 40海里B. 60海里C. 70海里D. 80海里
8. 如图，一条笔直的河L，牧马人从P地出发,到河边M处饮马，然后到Q地，现有如下四种方案，可使牧马人所走路径最短的是（ ）
A. B. C. D.
9. 下列说法中错误的是（ ）
A. 等腰三角形的高、中线、角平分线互相重合
B. 等腰三角形一腰上的高与底边的夹角等于顶角的一半
C. 轴对称图形的对应点所连线段被对称轴垂直平分
D. 三角形两边的垂直平分线的交点到三个顶点距离相等
二．填空题（每小题3分，共计27分）
10. 计算______．
11. 在中，若，则____________．
12. 已知点P(，3)与点Q(－2，)关于y轴对称，则+＝_________．
13. 计算：_______．
14. 如图，在中，垂直平分，交于点，则____________．
15. 如图，把一张矩形的纸片沿折叠，若，则的面积______．
16. 如图，在中，是等边三角形，若，则线段的长为______．
17. 等腰三角形一腰上的高与另一腰所成的夹角为，则这个等腰三角形的顶角为______．
18. 如图，平分，，交的延长线于点，，，则______．
三．解答题（19题6分，20题—24题各8分，25题，26题各10分，共计66分）
19. 计算：
（1）
（2）
20. 已知点
（1）若点关于轴对称，求值；
（2）若点关于轴对称，求的值．
21. 如图，三个顶点的坐标分别为．
（1）画出关于轴对称的，并写出点坐标；
（2）在轴上确定一点，连接，使最小，并直接写出点的坐标（保留作图痕迹）
22. 如图所示，是等边三角形，为中线，．
（1）求的度数；
（2）若，求的面积．
23. 已知：在中，D、E分别在、上，且，与交于点F，连接交BC于G．

（1）如图1，求证：；
（2）如图2，当时，直接写出所有等于的角．
24. 观察下列两个等式：，给出定义如下：我们称使成立的一对有理数为“共生有理数对”，记为，如数对都是“共生有理数对”．
（1）判断数对否为“共生有理数对”，并说明理由；
（2）若是“共生有理数对”，且，求的值；
（3）若是“共生有理数对”，且，求的值．
25. 综合与实践
【问题情境】数学活动课上，小明同学分享了一道题，如图1，在中，点分别在和上，且，求的度数．
（1）解答小明同学提出的问题．
【深入探究】李老师提出，连接交于点，当时，与有一定的数量关系；
（2）如图2，请你猜想与的数量关系并证明．
【拓展应用】兴趣小组在课余时间研究了这道题，并提出了新的问题，在（2）的条件下，若，求的长．
（3）请你解答兴趣小组提出的问题．
26. 如图，在平面直角坐标系中，点为坐标原点，的面积等于24．
（1）求点的坐标；
（2）动点从点出发，以每秒2个单位的速度沿x轴负方向运动，运动时间为t秒，过作轴垂线交直线于点，连接．若的面积为，求与的关系式；
（3）在（2）的条件下，过点作的垂线交轴于点，交于点，当时，在第一象限内是否存在点，使是以为腰的等腰直角三角形？若存在，请求出点，若不存在，请说明理由．