北师大版数学七上期末考点提升练习专题30 一元一次方程应用之销售盈亏问题（2份，原卷版+解析版）

这是一份北师大版数学七上期末考点提升练习专题30 一元一次方程应用之销售盈亏问题（2份，原卷版+解析版），文件包含北师大版数学七上期末考点提升练习专题30一元一次方程应用之销售盈亏问题原卷版doc、北师大版数学七上期末考点提升练习专题30一元一次方程应用之销售盈亏问题解析版doc等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
A．不赚不亏B．赚10元C．赔20元D．赚20元
【答案】C
【分析】设盈利的上衣的进价为x元，亏损的上衣的进价为y元，根据利润＝销售收入−成本，即可得出关于x（或y）的一元一次方程，解之即可得出两件上衣的成本，再利用总利润＝两件上衣的总售价−两件上衣的总成本即可求出结论．
【详解】解：设盈利的上衣的成本为x元，亏损的上衣的成本为y元，
依题意，得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
解得：x＝120，y＝200，
150＋150−120−200＝−20（元）．
∴该商贩亏损20元．
故选：C．
【点睛】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
2．已知某商店有两个进价不同的计算器，都卖了100 元，其中一个盈利 60% ，另一个亏损20%，在这次买卖中，这家商店（ ）
A．不盈不亏B．盈利 37.5 元C．亏损 25 元D．盈利 12.5 元
【答案】D
【分析】设盈利的计算器的进价为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，亏损的计算器的进价为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，用售价减去进价即可.
【详解】解：设盈利的计算器的进价为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，亏损的计算器的进价为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 元，所以这家商店盈利了12.5元..
故选：D
【点睛】本题考查了一元一次方程的应用，找准等量关系列出方程是解题的关键.
3．一件工艺品按成本价提高 SKIPIF 1 < 0 后，以 SKIPIF 1 < 0 元售出，则这件工艺品的利润是（ ）
A． SKIPIF 1 < 0 元B． SKIPIF 1 < 0 元C． SKIPIF 1 < 0 元D． SKIPIF 1 < 0 元
【答案】D
【分析】设成本为 SKIPIF 1 < 0 元，由题意可得等量关系： SKIPIF 1 < 0 成本价 SKIPIF 1 < 0 售价，进而得到方程，可算出成本价，再利用售价 SKIPIF 1 < 0 成本价 SKIPIF 1 < 0 利润．
【详解】解：设成本为 SKIPIF 1 < 0 元，由题意得：
SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0 ，
∴利润= SKIPIF 1 < 0 （元 SKIPIF 1 < 0 ，
故选： SKIPIF 1 < 0 ．
【点睛】此题主要考查了一元一次方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程．
4．一件商品按成本价提高30%后标价，又以8折销售，售价为416元，这件商品卖出后获得利润（ ）元．
A．16B．18C．24D．32
【答案】A
【分析】此题可设原价为x元，提高30%后标价，实际上是按原价的130%标价，又以8折销售是以原价的80%销售，根据题意列方程解答即可．
【详解】解：设原价为x元，根据题意列方程得：（1+30%）x×80%＝416，
解得x＝400，
416﹣400＝16（元），
即这件商品卖出后获得利润16元．
故选：A．
【点睛】本题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
5．某商场把进价为160元的商品按照8折出售，仍可获利 SKIPIF 1 < 0 ，则该商品的标价为______元．
【答案】220.
【分析】可以设标价为x元,列出方程解出即可.
【详解】设标价为x元,由题意得:
SKIPIF 1 < 0 =10%
解得:x=220.
故答案为:220.
【点睛】本题考查一元一次方程的应用,关键在于读题列出方程.
6．某件商品的标价是110元，按标价的八折销售时，仍可获利10%，则这件商品每件的进价为_____元．
【答案】80
【详解】解：设每件的进价是x元，由题意得：（1+10%）x=110×0.8，
解得x=80，
即每件的进价是80元
故答案为：80．
【点睛】本题考查一元一次方程的应用，掌握题目中的等量关系是解题关键．
7．据了解，个体服装销售要高出进价的20%方可盈利，一销售老板以高出进价的60%标价，如果一件服装标价240元，那么：
（1）进价是多少元？（2）最低售价多少元时，销售老板方可盈利？
【答案】（1）进价150元，(2)最低售价180.
【详解】试题分析：
（1）设进价为 SKIPIF 1 < 0 元/件，则标价可表示为 SKIPIF 1 < 0 ，根据标价为240元/件可列方程： SKIPIF 1 < 0 =240，解方程即可得到进价；
（2）设最低售价为 SKIPIF 1 < 0 元/件时，销售老板方看获利，结合（1）中所求进价即可根据题意列出算式，计算即可得到最低售价.
试题解析：
（1）设进价为 SKIPIF 1 < 0 元/件，根据题意可得：
SKIPIF 1 < 0 =240，
解得： SKIPIF 1 < 0 ，
答：这件衣服的进价为150元；
（2）设最低售价为 SKIPIF 1 < 0 元/件时，销售老板方可获利，根据题意可得：
SKIPIF 1 < 0 （元）.
答：最低售价为180元/件时，销售老板方可获利.
8．“双十一”期间，某电商决定对网上销售的商品一律打8折销售，张燕购买一台某种型号手机时发现，每台手机比打折前少支付500元，求每台该种型号手机打折前的售价．
【答案】2500元
【详解】试题分析：可设每台该种型号手机打折前的售价为x元，根据等量关系：每台手机比打折前少支付500元，列出方程求解即可．
解：设每台该种型号手机打折前的售价为x元，由题意得：
x﹣0.8x=500，
解得：x=2500．
答：每台该种型号手机打折前的售价为2500元．
考点：一元一次方程的应用．
9．贵阳市人民广场某超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的 SKIPIF 1 < 0 倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价－进价）
（1）该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（2）该超市第二次以第一次的进价又购进甲、乙两种商品．其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售．第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元，求第二次乙种商品是按原价打几折销售？
【答案】（1）1950（元）；（2）第二次乙商品是按原价打8.5折销售．
【分析】（1）设第一次购进甲种商品 SKIPIF 1 < 0 件，则购进乙种商品（ SKIPIF 1 < 0 ）件，根据单价×数量=总价，即可得出关于x的一元一次方程，可求得甲、乙两种商品得数量；根据总利润=单件利润×销售数量，列式计算即可求出结论；
（2）设第二次乙种商品是按原价打y折销售，根据总利润=单件利润×销售数量，即可得出关于y的一元一次方程，解之即可得出结论．
【详解】解：（1）设第一次购进甲种商品x件，则购进乙种商品（ SKIPIF 1 < 0 ）件，
根据题意得： SKIPIF 1 < 0
解得： SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 （件）．
∴（29-22）×150+（40-30）×90=1950（元）．
答：该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得利润1950元．
（2）设第二次乙种商品是按原价打y折销售，
根据题意得： SKIPIF 1 < 0 ，
解得：y=8.5．
答：第二次乙商品是按原价打8.5折销售．
【点睛】本题考查了一元一次方程的应用，解题的关键是：找准等量关系，正确列出一元一次方程.
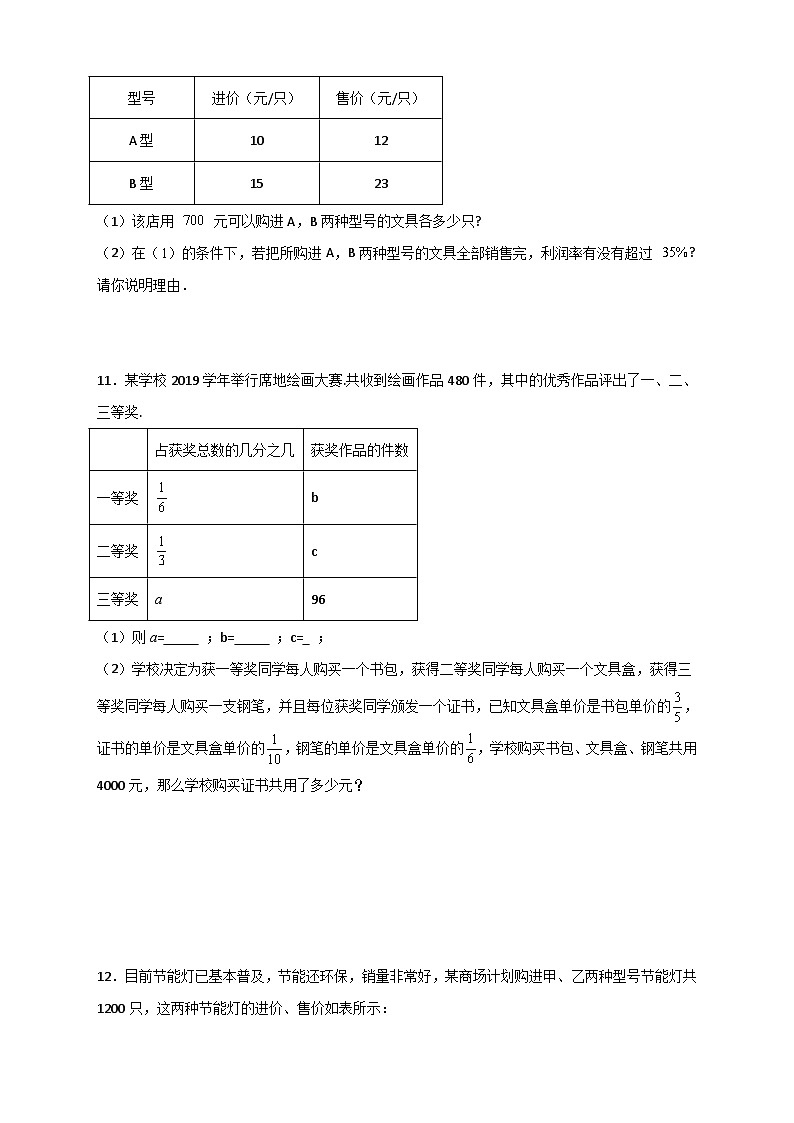
10．“元旦”期间，某文具店购进 SKIPIF 1 < 0 只两种型号的文具进行销售，其进价和售价如表：
（1）该店用 SKIPIF 1 < 0 元可以购进A，B两种型号的文具各多少只?
（2）在（ SKIPIF 1 < 0 ）的条件下，若把所购进A，B两种型号的文具全部销售完，利润率有没有超过 SKIPIF 1 < 0 ?请你说明理由．
【答案】（1） A型文具购进 SKIPIF 1 < 0 只，B型文具购进 SKIPIF 1 < 0 只；（2）利润率没有超过 SKIPIF 1 < 0 ．
【分析】（1） 设可以购进 SKIPIF 1 < 0 种型号的文具 SKIPIF 1 < 0 只， 则可以购进 SKIPIF 1 < 0 种型号的文具 SKIPIF 1 < 0 只， 根据总价 SKIPIF 1 < 0 单价 SKIPIF 1 < 0 数量结合 SKIPIF 1 < 0 、 SKIPIF 1 < 0 两种文具的进价及总价， 即可得出关于 SKIPIF 1 < 0 的一元一次方程， 解之即可得出结论；
（2） 根据总利润 SKIPIF 1 < 0 单价利润 SKIPIF 1 < 0 数量即可求出销售完这批货物的总利润， 用其除以进价 SKIPIF 1 < 0 再与 SKIPIF 1 < 0 比较后， 即可得出结论 ．
【详解】解：（1）设可以购进 SKIPIF 1 < 0 种型号的文具 SKIPIF 1 < 0 只， 则可以购进 SKIPIF 1 < 0 种型号的文具 SKIPIF 1 < 0 只，
根据题意得： SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0 ，
∴B型文具购进= SKIPIF 1 < 0 （只）．
答：A型文具购进 SKIPIF 1 < 0 只，B型文具购进 SKIPIF 1 < 0 只．
（2）总利润= SKIPIF 1 < 0 =210（元）；
SKIPIF 1 < 0 ，没有超过 SKIPIF 1 < 0 ．
答：利润率没有超过 SKIPIF 1 < 0 ．
【点睛】本题考查了一元一次方程的应用， 解题的关键是： （1） 根据总价 SKIPIF 1 < 0 单价 SKIPIF 1 < 0 数量列出关于 SKIPIF 1 < 0 的一元一次方程； （2） 根据总利润 SKIPIF 1 < 0 单件利润 SKIPIF 1 < 0 数量求出总利润 ．
11．某学校2019学年举行席地绘画大赛.共收到绘画作品480件，其中的优秀作品评出了一、二、三等奖.
（1）则a= ；b= ；c= ；
（2）学校决定为获一等奖同学每人购买一个书包，获得二等奖同学每人购买一个文具盒，获得三等奖同学每人购买一支钢笔，并且每位获奖同学颁发一个证书，已知文具盒单价是书包单价的 SKIPIF 1 < 0 ，证书的单价是文具盒单价的 SKIPIF 1 < 0 ，钢笔的单价是文具盒单价的 SKIPIF 1 < 0 ，学校购买书包、文具盒、钢笔共用4000元，那么学校购买证书共用了多少元？
【答案】（1） SKIPIF 1 < 0 ，b=32，c=64；（2）共用576元
【分析】（1）根据所给信息，计算一、二等奖占获奖总数的多少即可求出a，再根据题意列方程、再解方程即可求出b和c的值；
（2）设文具盒的单价为x元，然后表示出其他物品的单价，最后列出一元一次方程求解即可.
【详解】解：（1） SKIPIF 1 < 0
设获奖作品的件数为x件.
根据题意，得 SKIPIF 1 < 0 x=b， SKIPIF 1 < 0 x=c，ax=96，
解得：b=32，c=64
故答案为 SKIPIF 1 < 0 、32、64.
（）设文具盒的单价为x元，则钢笔的单价为 SKIPIF 1 < 0 x元，书包的单价为x÷ SKIPIF 1 < 0 = SKIPIF 1 < 0 x元，证书的
价为 SKIPIF 1 < 0 x元.根据题意，得
32× SKIPIF 1 < 0 x +64x+96× SKIPIF 1 < 0 x=4000
解得x=30
则证书共用了192× SKIPIF 1 < 0 x=192× SKIPIF 1 < 0 ×30=576.
答：学年购买证书共用576元.
【点睛】本题考查了一元一次方程的应用，根据表格所给信息，设合适的未知数并表示其它量是解答本题的关键.
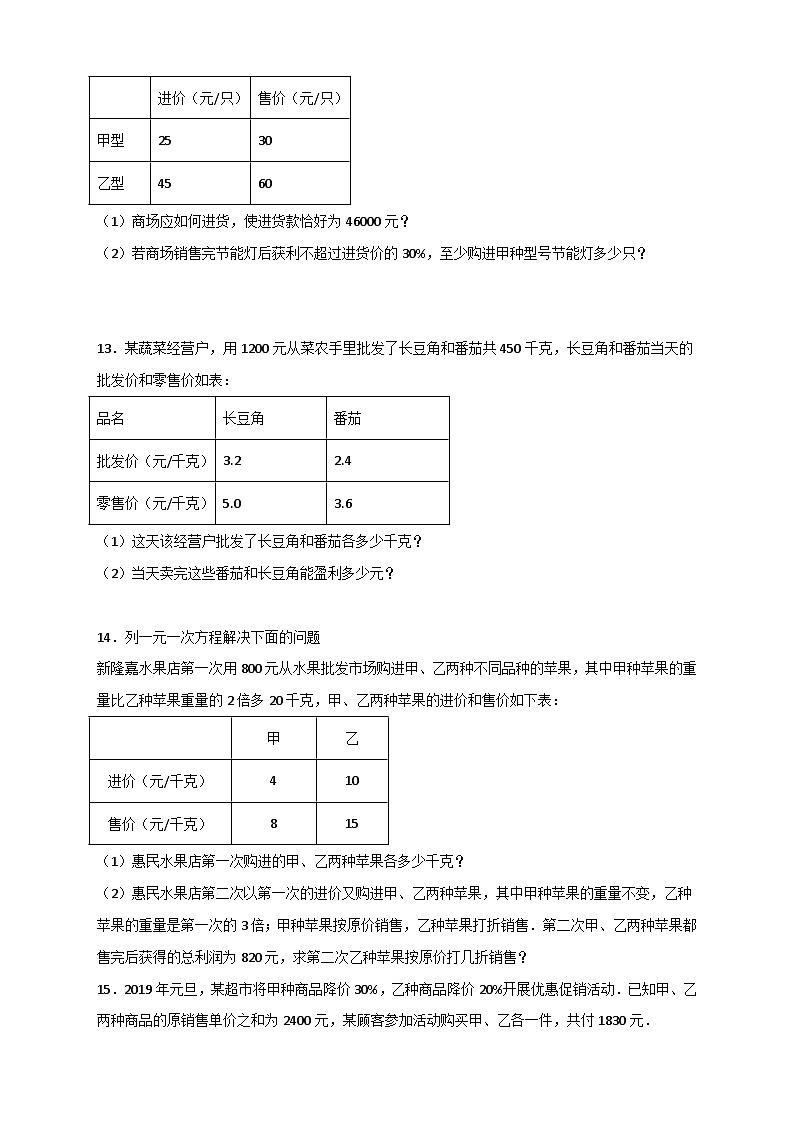
12．目前节能灯已基本普及，节能还环保，销量非常好，某商场计划购进甲、乙两种型号节能灯共1200只，这两种节能灯的进价、售价如表所示：
（1）商场应如何进货，使进货款恰好为46000元？
（2）若商场销售完节能灯后获利不超过进货价的30%，至少购进甲种型号节能灯多少只？
【答案】（1）购进甲型节能灯400只，购进乙型节能灯800只进货款恰好为46000元；（2）商场购进甲型节能灯450只，购进乙型节能灯750只时利润为13500元．
【分析】（1）设购进甲型节能灯x只，乙型节能灯y只，根据“总数量为1200只、进货款恰好为46000元”列方程组求解可得；
（2）设商场购进甲型节能灯a只，则购进乙型节能灯（1200-a）只，根据“获利最多不超过进货价的30%”列出不等式求解可得．
【详解】解：（1）设购进甲型节能灯x只，乙型节能灯y只，
根据题意，得： SKIPIF 1 < 0
解得： SKIPIF 1 < 0 ，
答：购进甲型节能灯400只，乙型节能灯800只，进货款恰好为46000元；
（2）设商场购进甲型节能灯a只，则购进乙型节能灯（1200﹣a）只，由题意，
得：（30﹣25）a+（60﹣45）（1200﹣a）≤[25a+45（1200﹣a）]×30%，
解得：a≥450．
答：至少购进甲种型号节能灯450只．
【点睛】此题主要考查了二元一次方程组和一元一次不等式的应用，关键是正确理解题意，找出题目中的等量关系和不等关系，设出未知数，列出方程与不等式．
13．某蔬菜经营户，用1200元从菜农手里批发了长豆角和番茄共450千克，长豆角和番茄当天的批发价和零售价如表：
（1）这天该经营户批发了长豆角和番茄各多少千克？
（2）当天卖完这些番茄和长豆角能盈利多少元？
【答案】（1）这天该经营户批发了长豆角150千克，则批发了番茄300千克，（2）能盈利630元．
【分析】（1）设这天该经营户批发了长豆角x千克，则批发了番茄（450﹣x）千克，根据图表所示，列出关于x的一元一次方程，解之即可，
（2）根据“总利润=长豆角的单位利润×数量+番茄的单位利润×数量”，结合（1）的答案，列式计算即可．
【详解】解：（1）设这天该经营户批发了长豆角x千克，则批发了番茄（450﹣x）千克，
根据题意得：
3.2x+2.4（450﹣x）=1200，
解得：x=150，
450﹣150=300（千克），
答：这天该经营户批发了长豆角150千克，则批发了番茄300千克，
（2）根据题意得：
（5﹣3.2）×150+（3.6﹣2.4）×300
=1.8×150+1.2×300
=630（元），
答：当天卖完这些番茄和长豆角能盈利630元．
【点睛】本题考查了一元一次方程的应用，正确找出等量关系，列出一元一次方程即可．
14．列一元一次方程解决下面的问题
新隆嘉水果店第一次用800元从水果批发市场购进甲、乙两种不同品种的苹果，其中甲种苹果的重量比乙种苹果重量的2倍多20千克，甲、乙两种苹果的进价和售价如下表：
（1）惠民水果店第一次购进的甲、乙两种苹果各多少千克？
（2）惠民水果店第二次以第一次的进价又购进甲、乙两种苹果，其中甲种苹果的重量不变，乙种苹果的重量是第一次的3倍；甲种苹果按原价销售，乙种苹果打折销售．第二次甲、乙两种苹果都售完后获得的总利润为820元，求第二次乙种苹果按原价打几折销售？
【答案】第一次购进甲种苹果100千克，购进乙种苹果40千克；（2）第二次乙种苹果按原价9折出售．
【分析】（1）设第一次购进乙种苹果 SKIPIF 1 < 0 千克，则购进甲种苹果( SKIPIF 1 < 0 )千克，根据“第一次购进甲、乙两种苹果用800元”即可列出关于x的方程，解方程即可求出答案；
（2）先求出第二次的总进价，再设第二次乙种苹果按原价 SKIPIF 1 < 0 折销售，然后根据“甲、乙两种苹果的总售价－总进价=利润820元”列出关于y的方程，解方程即得结果．
【详解】（1）解：设第一次购进乙种苹果 SKIPIF 1 < 0 千克，则购进甲种苹果( SKIPIF 1 < 0 )千克．
根据题意，得 SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；
答：第一次购进甲种苹果100千克，购进乙种苹果40千克．
（2）解：第二次购进乙苹果 SKIPIF 1 < 0 千克，
总进价= SKIPIF 1 < 0 元，
设第二次乙种苹果按原价 SKIPIF 1 < 0 折销售，根据题意，得
SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ；
答：第二次乙种苹果按原价9折出售．
【点睛】本题考查了一元一次方程的应用，正确理解题意、找准相等关系是解题的关键．
15．2019年元旦，某超市将甲种商品降价30%，乙种商品降价20%开展优惠促销活动．已知甲、乙两种商品的原销售单价之和为2400元，某顾客参加活动购买甲、乙各一件，共付1830元．
(1)甲、乙两种商品原销售单价各是多少元？
(2)若商场在这次促销活动中甲种商品亏损25%，乙种商品盈利25%，那么商场在这次促销活动中是盈利还是亏损了？如果是盈利，求商场销售甲、乙两种商品各一件盈利了多少元？如果是亏损，求销售甲、乙两种商品各一件亏损了多少元？
【答案】（1）甲商品原销售单价为900元，乙商品的原销售单价为1500元．（2）商场在这次促销活动中盈利，盈利了30元．
【详解】试题分析：（1）设甲商品原单价为x元，则乙商品原单价为（2400-x）元，由某顾客参加活动购买甲、乙各一件，共付1830元．列方程，解答即可；
（2）设甲商品进价为a元，乙商品进价为b元，由商场在这次促销活动中甲种商品亏损25%，乙种商品盈利25%，列方程解出a，b，然后根据利润=售价－进价，即可判断．
试题解析：解：（1）设甲商品原单价为x元，则乙商品原单价为（2400-x）元，由题意得：
（1－30%）x+（1－20%）（2400－x）=1830
解得：x=900，则2400－x=1500．
答：甲商品原单价为900元，则乙商品原单价为1500元．
（2）设甲商品进价为a元，乙商品进价为b元，由题意得：
（1-25%）a=（1-30%）×900，（1+25%）b=（1-20%）×1500
解得：a=840，b=960．
∵1830－（840+960）=30，∴盈利了30元．
答：盈利，且盈利了30元．
16．列方程式应用题．
天河食品公司收购了200吨新鲜柿子，保质期15天，该公司有两种加工技术，一种是加工为普通柿饼，另一种是加工为特级霜降柿饼，也可以不需加工直接销售．相关信息见表：
由于生产条件的限制，两种加工方式不能同时进行，为此公司研制了两种可行方案：
方案1：尽可能多地生产为特级霜降柿饼，没来得及加工的新鲜柿子，在市场上直接销售；
方案2：先将部分新鲜柿子加工为特级霜降柿饼，再将剩余的新鲜柿子加工为普通柿饼，恰好15天完成．
请问：哪种方案获利更多？获利多少元？
【答案】方案二获利更多，获利1120000元
【分析】根据利润＝单价×数量可直接求出方案一所获利润；根据题意列方程求出方案二加工为特级霜降柿饼的吨数和加工为普通柿饼的吨数，然后根据利润＝单价×数量求出方案二所获利润，进行比较即可判断．
【详解】解：方案一：15×8×8000+（200﹣15×8）×1000＝1040000（元），
∴尽可能多地生产为特级霜降柿饼，没来得及加工的新鲜柿子，在市场上直接销售，可获利润1040000元；
方案二：设加工为特级霜降柿饼x吨，则加工为普通柿饼（200﹣x）吨，
由题意可得： SKIPIF 1 < 0 ，
解得x＝40，
∴200﹣x＝160，
∴利润为：40×8000+160×5000＝1120000（元）
∴该公司可以加工为特级霜降柿饼40吨，加工为普通柿饼160吨，可获得利润为1120000元．
∵1120000＞1040000，
∴方案二获利更多，获利1120000元.
【点睛】本题考查了一元一次方程的应用．此题中的数量关系较多，正确理解题意是解决此题的重点．
17．引进扶贫产品， 丰富市民菜篮子．为了完成新时代脱贫攻坚的目标任务， 某市商务局近些年致力于帮扶地区特色产品走进市民的菜篮子．该市帮助扶贫产品和市场需求有效对接， 实现了农产品的特色化、品牌化， 助力更多优质农产品走出了地区、走向了全国．已知该市去年和今年两年的“明星”扶贫农产品销售总额为179.8万，其中“明星”扶贫农产品去年的价格为16元/千克， 今年的价格为12元/千克， 今年的销售产量比去年增长了25 SKIPIF 1 < 0 ．
（1）请问今年的“明星”扶贫农产品销售了多少千克？
（2）为了促进该地区滞销农产品的销售， 现市商务局决定采用直播带货的方式进行销售．某电商平台采取分段收取“坑位费”的计算方法， 如市商务局“直播带货”销售农产品的销售额不超过20万的部分按 SKIPIF 1 < 0 交给电商公司， 超过20万不超过50万的部分按 SKIPIF 1 < 0 交给电商公司， 超过50万的部分按 SKIPIF 1 < 0 的比例交给电商公司．已知此次直播扣除坑位费的销售额为643700元 ， 则这次直播未扣除坑位费的销售额为多少？
【答案】（1） SKIPIF 1 < 0 千克；（2） SKIPIF 1 < 0 万元
【分析】（1）设今年的“明星”扶贫农产品销售了 SKIPIF 1 < 0 千克， 则去年的“明星”扶贫农产品销售了 SKIPIF 1 < 0 千克，然后根据该市去年和今年两年的“明星”扶贫农产品销售总额为179.8万，列出方程求解即可；
（2）设这次直播未扣除坑位费的销售额为 SKIPIF 1 < 0 万元．由此次直播扣除坑位费的销售额为64.37万元， 则此次直播未扣除坑位费的销售额 SKIPIF 1 < 0 一定大于50万，由此根据题意列出方程求解即可．
【详解】解：（1）设今年的“明星”扶贫农产品销售了 SKIPIF 1 < 0 千克， 则去年的“明星”扶贫农产品销售了 SKIPIF 1 < 0 千克，
根据题意得， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0 ．
答：今年的“明星”扶贫农产品销售了 SKIPIF 1 < 0 千克
（2）设这次直播未扣除坑位费的销售额为 SKIPIF 1 < 0 万元．
∵此次直播扣除坑位费的销售额为64.37万元，
∴此次直播未扣除坑位费的销售额 SKIPIF 1 < 0 一定大于50万，
由题意得： SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ，
答：这次直播未扣除坑位费的销售额为 SKIPIF 1 < 0 万元．
【点睛】本题主要考查了一元一次方程的应用，解题的关键在于能够根据题意列出方程求解．
甲
乙
进价（元/件）
22
30
售价（元/件）
29
40
型号
进价（元/只）
售价（元/只）
A型
10
12
B型
15
23
占获奖总数的几分之几
获奖作品的件数
一等奖
SKIPIF 1 < 0
b
二等奖
SKIPIF 1 < 0
c
三等奖
a
96
进价（元/只）
售价（元/只）
甲型
25
30
乙型
45
60
品名
长豆角
番茄
批发价（元/千克）
3.2
2.4
零售价（元/千克）
5.0
3.6
甲
乙
进价（元/千克）
4
10
售价（元/千克）
8
15
品种
每天可加工数量（吨）
每吨获利（元）
新鲜柿子
不需加工
1000元
普通柿饼
16吨
5000元
特级霜降柿饼
8吨
8000元
销售额 SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
“坑位费”收取比例
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0