中考数学一轮复习重点考向练习突破02 方程（组）、不等式、函数等代数应用题（2份，原卷版+解析版）

这是一份中考数学一轮复习重点考向练习突破02 方程（组）、不等式、函数等代数应用题（2份，原卷版+解析版），文件包含中考数学一轮复习重点考向练习突破02方程组不等式函数等代数应用题教师版doc、中考数学一轮复习重点考向练习突破02方程组不等式函数等代数应用题原卷版doc等2份试卷配套教学资源，其中试卷共59页， 欢迎下载使用。
目录一览
代数应用题以实际问题为背景，一般为生活中常见的分析决策问题.该题型借鉴PISA理念，考查数学抽象和数学建模以及阅读能力，学会把实际问题变成数学问题，用数学符号建立方程（组）、不等式、函数等表示数学问题中的数量关系，并设计出适当的解决问题的方案，培养应用意识和模型思想，提高解决实际问题的能力.
►考向一 购买、分配类问题
1．（2023·淄博）某古镇为发展旅游产业，吸引更多的游客前往游览，助力乡村振兴，决定在“五一”期间对团队*旅游实行门票特价优惠活动，价格如下表：
*题中的团队人数均不少于10人
现有甲、乙两个团队共102人，计划利用“五一”假期到该古镇旅游，其中甲团队不足50人，乙团队多于50人．
（1）如果两个团队分别购票，一共应付5580元，问甲、乙团队各有多少人？
（2）如果两个团队联合起来作为一个“大团队”购票，比两个团队各自购票节省的费用不少于1200元，问甲团队最少多少人？
2．（2023·雅安）李叔叔批发甲、乙两种蔬菜到菜市场去卖，已知甲、乙两种蔬菜的批发价和零售价如下表所示：
（1）若他批发甲、乙两种蔬菜共 SKIPIF 1 < 0 花 SKIPIF 1 < 0 元．求批发甲乙两种蔬菜各多少千克？（列方程或方程组求解）
（2）若他批发甲、乙两种蔬菜共 SKIPIF 1 < 0 花m元，设批发甲种蔬菜 SKIPIF 1 < 0 ，求m与n的函数关系式；
（3）在（2）的条件下，全部卖完蔬菜后要保证利润不低于 SKIPIF 1 < 0 元，至少批发甲种蔬菜多少千克？
3．（2023·湘潭）我国航天事业发展迅速，2023年5月30日9时31分，神舟十六号载人飞船成功发射，某玩具店抓住商机，先购进了1000件相关航天模型玩具进行试销，进价为50元/件．
（1）设每件玩具售价为x元，全部售完的利润为y元．求利润y（元）关于售价x（元/件）的函数表达式；
（2）当售价定为60元/件时，该玩具销售火爆，该店继续购进一批该种航天模型玩具，并从中拿出这两批玩具销售利润的20%用于支持某航模兴趣组开展活动，在成功销售完毕后，资助经费恰好10000元，请问该商店继续购进了多少件航天模型玩具？
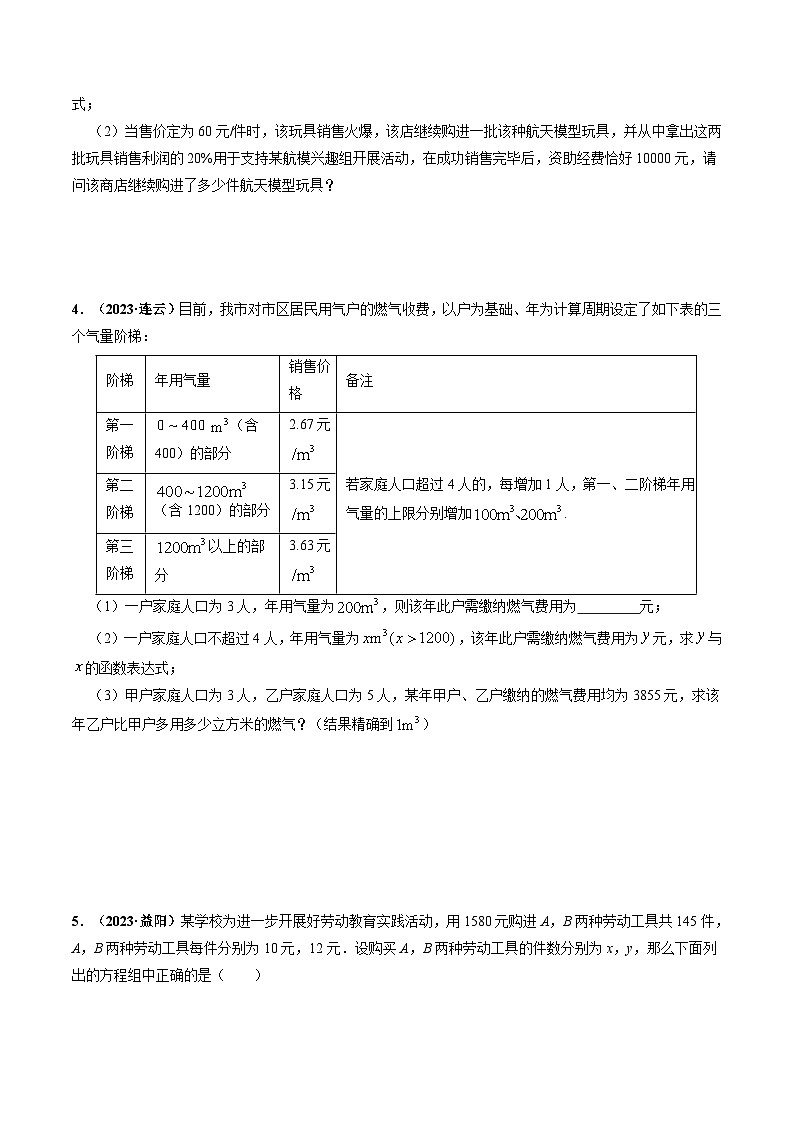
4．（2023·连云）目前，我市对市区居民用气户的燃气收费，以户为基础、年为计算周期设定了如下表的三个气量阶梯：
（1）一户家庭人口为3人，年用气量为 SKIPIF 1 < 0 ，则该年此户需缴纳燃气费用为 元；
（2）一户家庭人口不超过4人，年用气量为 SKIPIF 1 < 0 ，该年此户需缴纳燃气费用为 SKIPIF 1 < 0 元，求与的函数表达式；
（3）甲户家庭人口为3人，乙户家庭人口为5人，某年甲户、乙户缴纳的燃气费用均为3855元，求该年乙户比甲户多用多少立方米的燃气？（结果精确到 SKIPIF 1 < 0 ）
5．（2023·益阳）某学校为进一步开展好劳动教育实践活动，用1580元购进A，B两种劳动工具共145件，A，B两种劳动工具每件分别为10元，12元．设购买A，B两种劳动工具的件数分别为x，y，那么下面列出的方程组中正确的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．（2023·日照）要制作200个A，B两种规格的顶部无盖木盒，A种规格是长、宽、高都为 SKIPIF 1 < 0 的正方体无盖木盒，B种规格是长、宽、高各为，， SKIPIF 1 < 0 的长方体无盖木盒，如图1．现有200张规格为 SKIPIF 1 < 0 的木板材，对该种木板材有甲、乙两种切割方式，如图2．切割、拼接等板材损耗忽略不计．
（1）设制作A种木盒x个，则制作B种木盒 个；若使用甲种方式切割的木板材y张，则使用乙种方式切割的木板材 张；
（2）该200张木板材恰好能做成200个A和B两种规格的无盖木盒，请分别求出A，B木盒的个数和使用甲，乙两种方式切割的木板材张数；
（3）包括材质等成本在内，用甲种切割方式的木板材每张成本5元，用乙种切割方式的木板材每张成本8元．根据市场调研，A种木盒的销售单价定为a元，B种木盒的销售单价定为 SKIPIF 1 < 0 元，两种木盒的销售单价均不能低于7元，不超过18元．在（2）的条件下，两种木盒的销售单价分别定为多少元时，这批木盒的销售利润最大，并求出最大利润．
7．（2023·青岛）某服装店经销A，B两种T恤衫，进价和售价如下表所示：
（1）第一次进货时，服装店用6000元购进A，B两种T恤衫共120件，全部售完获利多少元？
（2）受市场因素影响，第二次进货时，A种T恤衫进价每件上涨了5元，B种T恤衫进价每件上涨了10元，但两种T恤衫的售价不变．服装店计划购进A，B两种T恤衫共150件，且B种T恤衫的购进量不超过A种T恤衫购进量的2倍．设此次购进A种T恤衫m件，两种T恤衫全部售完可获利W元．
①请求出W与m的函数关系式；
②服装店第二次获利能否超过第一次获利？请说明理由．
8．（2023·娄底）为落实“五育并举”，绿化美化环境，学校在劳动周组织学生到校园周边种植甲、乙两种树苗．已知购买甲种树苗3棵，乙种树苗2棵共需12元；购买甲种树苗1棵，乙种树苗3棵共需11元．
（1）求每棵甲、乙树苗的价格．
（2）本次活动共种植了200棵甲、乙树苗，假设所种的树苗若干年后全部长成了参天大树，并且平均每棵树的价值（含生态价值，经济价值）均为原来树苗价的100倍，要想获得不低于5万元的价值，请问乙种树苗种植数量不得少于多少棵？
9．（2023·广安）“广安盐皮蛋”是小平故里的名优特产，某超市销售 SKIPIF 1 < 0 两种品牌的盐皮蛋，若购买9箱种盐皮蛋和6箱种盐皮蛋共需390元；若购买5箱种盐皮蛋和8箱种盐皮蛋共需310元．
（1）种盐皮蛋、种盐皮蛋每箱价格分别是多少元？
（2）若某公司购买两种盐皮蛋共30箱，且种的数量至少比种的数量多5箱，又不超过种的2倍，怎样购买才能使总费用最少？并求出最少费用．
10．（2023·丹东）某品牌大米远近闻名，深受广大消费者喜爱，某超市每天购进一批成本价为每千克元的该大米，以不低于成本价且不超过每千克 SKIPIF 1 < 0 元的价格销售 SKIPIF 1 < 0 当每千克售价为 SKIPIF 1 < 0 元时，每天售出大米 SKIPIF 1 < 0 ；当每千克售价为 SKIPIF 1 < 0 元时，每天售出大米 SKIPIF 1 < 0 ，通过分析销售数据发现：每天销售大米的数量 SKIPIF 1 < 0 与每千克售价 SKIPIF 1 < 0 元 SKIPIF 1 < 0 满足一次函数关系．
（1）请直接写出与的函数关系式；
（2）超市将该大米每千克售价定为多少元时，每天销售该大米的利润可达到 SKIPIF 1 < 0 元？
（3）当每千克售价定为多少元时，每天获利最大？最大利润为多少？
11．（2023·黄冈）加强劳动教育，落实五育并举．孝礼中学在当地政府的支持下，建成了一处劳动实践基地.2023年计划将其中 SKIPIF 1 < 0 的土地全部种植甲乙两种蔬菜．经调查发现：甲种蔬菜种植成本y（单位；元/ SKIPIF 1 < 0 ）与其种植面积x（单位：）的函数关系如图所示，其中 SKIPIF 1 < 0 ；乙种蔬菜的种植成本为50元/．
（1）当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 元/；
（2）设2023年甲乙两种蔬菜总种植成本为W元，如何分配两种蔬菜的种植面积，使W最小？
（3）学校计划今后每年在这土地上，均按（2）中方案种植蔬菜，因技术改进，预计种植成本逐年下降，若甲种蔬菜种植成本平均每年下降 SKIPIF 1 < 0 ，乙种蔬菜种植成本平均每年下降 SKIPIF 1 < 0 ，当a为何值时，2025年的总种植成本为 SKIPIF 1 < 0 元？
12．（2022·东营）为满足顾客的购物需求，某水果店计划购进甲、乙两种水果进行销售.经了解，甲水果的进价比乙水果的进价低20%，水果店用1000元购进甲种水果比用1200元购进乙种水果的重量多10千克，已知甲，乙两种水果的售价分别为6元/千克和8元/千克.
（1）求甲、乙两种水果的进价分别是多少？
（2）若水果店购进这两种水果共150千克，其中甲种水果的重量不低于乙种水果重量的2倍，则水果店应如何进货才能获得最大利润，最大利润是多少？
13．（2023·广州）因活动需要购买某种水果，数学活动小组的同学通过市场调查得知：在甲商店购买该水果的费用 SKIPIF 1 < 0 元与该水果的质量千克之间的关系如图所示；在乙商店购买该水果的费用 SKIPIF 1 < 0 元与该水果的质量千克之间的函数解析式为 SKIPIF 1 < 0 ．
（1）求 SKIPIF 1 < 0 与之间的函数解析式；
（2）现计划用 SKIPIF 1 < 0 元购买该水果，选甲、乙哪家商店能购买该水果更多一些？
14．（2023·湘西）2023年“地摊经济”成为社会关注的热门话题，“地摊经济”有着启动资金少、管理成本低等优点，特别是在受到疫情冲击后的经济恢复期，“地摊经济”更是成为许多创业者的首选，甲经营了某种品牌小电器生意，采购2台A种品牌小电器和3台B种品牌小电器，共需要90元；采购3台A种品牌小电器和1台B种品牌小电器，共需要65元，销售一台A种品牌小电器获利3元，销售一台B种品牌小电器获利4元．
（1）求购买1台A种品牌小电器和1台B种品牌小电器各需要多少元？
（2）甲用不小于2750元，但不超过2850元的资金一次性购进A、B两种品牌小电器共150台，求购进A种品牌小电器数量的取值范围．
（3）在（2）的条件下，所购进的A、B两种品牌小电器全部销售完后获得的总利润不少于565元，请说明甲合理的采购方案有哪些？并计算哪种采购方案获得的利润最大，最大利润是多少？
►考向二 工程、行程类问题
15．（2023·淮安）快车和慢车同时从甲地出发，以各自的速度匀速向乙地行驶，快车到达乙地卸装货物用时 SKIPIF 1 < 0 ，结束后，立即按原路以另一速度匀速返回，直至与慢车相遇，已知慢车的速度为 SKIPIF 1 < 0 ．两车之间的距离 SKIPIF 1 < 0 与慢车行驶的时间 SKIPIF 1 < 0 的函数图象如图所示．
（1）请解释图中点的实际意义；
（2）求出图中线段 SKIPIF 1 < 0 所表示的函数表达式；
（3）两车相遇后，如果快车以返回的速度继续向甲地行驶，求到达甲地还需多长时间．
16．（2023·绥化）某校组织师生参加夏令营活动，现准备租用A、B两型客车（每种型号的客车至少租用一辆）.A型车每辆租金500元，B型车每辆租金600元.若5辆A型和2辆B型车坐满后共载客310人；3辆A型和4辆B型车坐满后共载客340人.
（1）每辆A型车、B型车坐满后各载客多少人？
（2）若该校计划租用A型和B型两种客车共10辆，总租金不高于5500元，并将全校420人载至目的地.该校有几种租车方案？哪种租车方案最省钱？
（3）在这次活动中，学校除租用A、B两型客车外，又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米，甲车从学校出发0.5小时后，乙车才从学校出发，却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s（千米）与甲车行驶的时间t（小时）之间的函数图象.根据图象信息，求甲乙两车第一次相遇后，t为何值时两车相距25千米.
17．（2023·呼和浩特）甲、乙两船从相距 SKIPIF 1 < 0 的，两地同时匀速沿江出发相向而行，甲船从地顺流航行 SKIPIF 1 < 0 时与从地逆流航行的乙船相遇甲、乙两船在静水中的航速均为 SKIPIF 1 < 0 ，则江水的流速为 SKIPIF 1 < 0 ．
18．（2023·南通）为推进全民健身设施建设，某体育中心准备改扩建一块运动场地．现有甲、乙两个工程队参与施工，具体信息如下：
信息—
信息二
甲工程队施工 SKIPIF 1 < 0 所需天数与乙工程队施工 SKIPIF 1 < 0 所需天数相等．
（1）求x的值；
（2）该工程计划先由甲工程队单独施工若干天，再由乙工程队单独继续施工，两队共施工22天，且完成的施工面积不少于 SKIPIF 1 < 0 ．该段时间内体育中心至少需要支付多少施工费用?
19．（2023·武汉）我国古代数学经典著作《九章算术》记载：“今有善行者行一百步，不善行者行六十步．今不善行者先行一百步，善行者追之，问几何步及之？”如图是善行者与不善行者行走路程 SKIPIF 1 < 0 （单位：步）关于善行者的行走时间 SKIPIF 1 < 0 的函数图象，则两图象交点 SKIPIF 1 < 0 的纵坐标是 ．
►考向三 销售、利润类问题
20．（2019·天水）一名在校大学生利用“互联网+”自主创业，销售一种产品，这种产品的成本价10元/件，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于16元/件，市场调查发现，该产品每天的销售量 （件 SKIPIF 1 < 0 与销售价 （元/件）之间的函数关系如图所示．
（1）求 与 之间的函数关系式，并写出自变量 的取值范围；
（2）求每天的销售利润W（元 与销售价 （元/件）之间的函数关系式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？
21．（2023·宿迁）某商场销售两种商品，每件进价均为20元．调查发现，如果售出种20件，种10件，销售总额为840元；如果售出种10件，种15件，销售总额为660元．
（1）求两种商品的销售单价．
（2）经市场调研，种商品按原售价销售，可售出40件，原售价每降价1元，销售量可增加10件；种商品的售价不变，种商品售价不低于种商品售价．设种商品降价元，如果两种商品销售量相同，求取何值时，商场销售两种商品可获得总利润最大？最大利润是多少？
22．（2023·湖州）某水产经销商以每千克30元的价格购进一批某品种淡水鱼，由销售经验可知，这种淡水鱼的日销售量y（千克）与销售价格x（元/千克）（30≤x＜60）存在一次函数关系，部分数据如表所示：
（1）试求出y关于x的函数表达式．
（2）设该经销商销售这种淡水鱼的日销售利润为W元，如果不考虑其他因素，求当销售价格x为多少时，日销售利润W最大？最大的日销售利润是多少元？
23．（2023·黄石）某工厂计划从现在开始，在每个生产周期内生产并销售完某型号设备，该设备的生产成本为 SKIPIF 1 < 0 万元 SKIPIF 1 < 0 件 SKIPIF 1 < 0 设第 SKIPIF 1 < 0 个生产周期设备的售价为 SKIPIF 1 < 0 万元件，售价与之间的函数解析式是 SKIPIF 1 < 0 ，其中是正整数当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
（1）求 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的值；
（2）设第个生产周期生产并销售完设备的数量为 SKIPIF 1 < 0 件，且与满足关系式 SKIPIF 1 < 0 ．
SKIPIF 1 < 0 当 SKIPIF 1 < 0 时，工厂第几个生产周期获得的利润最大？最大的利润是多少万元？
SKIPIF 1 < 0 当 SKIPIF 1 < 0 时，若有且只有 SKIPIF 1 < 0 个生产周期的利润不小于 SKIPIF 1 < 0 万元，求实数的取值范围．
24．（2023·哈尔滨）佳衣服装厂给某中学用同样的布料生产 SKIPIF 1 < 0 ， SKIPIF 1 < 0 两种不同款式的服装，每套款服装所用布料的米数相同，每套款服装所用布料的米数相同，若 SKIPIF 1 < 0 套款服装和 SKIPIF 1 < 0 套款服装需用布料 SKIPIF 1 < 0 米，套款服装和套款服装需用布料 SKIPIF 1 < 0 米．
（1）求每套款服装和每套款服装需用布料各多少米；
（2）该中学需要，两款服装共 SKIPIF 1 < 0 套，所用布料不超过 SKIPIF 1 < 0 米，那么该服装厂最少需要生产多少套款服装？
25．（2023·抚顺）电商平台销售某款儿童组装玩具，进价为每件100元，在销售过程中发现，每周的销售量y（件）与每件玩具售价x（元）之间满足一次函数关系（其中 SKIPIF 1 < 0 ，且x为整数）．当每件玩具售价为120元时，每周的销量为80件；当每件玩具售价为140元时，每周的销量为40件．
（1）求y与x之间的函数关系式；
（2）当每件玩具售价为多少元时，电商平台每周销售这款玩具所获的利润最大？最大周利润是多少元？
►考向四 最优方案问题
26．（2023·河南）某健身器材专卖店推出两种优惠活动，并规定购物时只能选择其中一种．
活动一：所购商品按原价打八折；
活动二：所购商品按原价每满300元减80元．（如：所购商品原价为300元，可减80元，需付款220元；所购商品原价为770元，可减160元，需付款610元）
（1）购买一件原价为450元的健身器材时，选择哪种活动更合算？请说明理由．
（2）购买一件原价在500元以下的健身器材时，若选择活动一和选择活动二的付款金额相等，求一件这种健身器材的原价．
（3）购买一件原价在900元以下的健身器材时，原价在什么范围内，选择活动二比选择活动一更合算？设一件这种健身器材的原价为a元，请直接写出a的取值范围．
27．（2023·通州模拟）某学校带领 SKIPIF 1 < 0 名学生到农场参加植树劳动，学校同时租用，， SKIPIF 1 < 0 三种型号客车去农场，其中，，三种型号客车载客量分别为 SKIPIF 1 < 0 人、 SKIPIF 1 < 0 人、人，租金分别为 SKIPIF 1 < 0 元、 SKIPIF 1 < 0 元、 SKIPIF 1 < 0 元为了节省资金，学校要求每辆车必须满载，并将学生一次性送到农场植树，请你写出一种满足要求的租车方案 ，满足要求的几种租车方案中，最低租车费用是 元
28．（2023·河西模拟） 天津农业大学的大学生参加助农活动，帮助果农销售砂糖桔砂糖桔的销售分为线上和线下两种销售方式，具体费用标准如下：线下销售方式： SKIPIF 1 < 0 元千克：线上销售方式：质量不超过千克时，每千克 SKIPIF 1 < 0 元，质量超过千克时，超出部分每千克按五折出售设购买砂糖桔千克，所需费用为元，可知两种销售方式的与之间的函数关系大致如图所示．
（1）根据题意，填写表格：
（2）请直接写出这两种销售方式对应的函数表达式；
（3）请问如何选择购买方式更省钱？为什么？
29．（2023·新余模拟）为弘扬学生“为人民服务”的精神，月份我区共青团委举办了“弘扬雷锋精神争做美德少年”主题演讲比赛比赛前购买了，两种装饰品对比赛场地进行了美化已知用元购买种装饰品与用 SKIPIF 1 < 0 元购买种装饰品的数量相等，且每个种装饰品的价格比种多元．
（1）A，B两种装饰品的单价各为多少元？
（2）计划购买，两种装饰品共个，其中种装饰品的数量不低于种装饰品的 SKIPIF 1 < 0 ，且不超过种装饰品数量的 SKIPIF 1 < 0 ，请求出共有几种购买方案？
30．（2023·红花岗模拟） 为拓展学生视野，促进书本知识与生活实践的深度融合，某中学组织九年级全体学生前往某研学基地开展研学活动，在此次活动中，若每位老师带队名学生，则还剩名学生没老师带；若每位老师带队 SKIPIF 1 < 0 名学生，就有一位老师少带名学生学校计划此次研学活动共租 SKIPIF 1 < 0 辆车，租金总费用不超过 SKIPIF 1 < 0 元现有甲、乙两种大型客车，它们的载客量和租金如下表所示：
（1）参加此次研学活动的老师和学生各有多少人？
（2）学校共有几种租车方案？最少租车费用是多少？
31．（2023·朝阳模拟） 一个 SKIPIF 1 < 0 人的旅游团到一家酒店住宿，酒店的客房只剩下间一人间和若干间三人间，住宿价格是一人间每晚元，三人间每晚 SKIPIF 1 < 0 元 SKIPIF 1 < 0 说明：男士只能与男士同住，女士只能与女士同住，三人间客房可以不住满，但每间每晚仍需支付元 SKIPIF 1 < 0
（1）若该旅游团一晚的住宿房费为 SKIPIF 1 < 0 元，则他们租住了 间一人间；
（2）若该旅游团租住了间一人间，且共有 SKIPIF 1 < 0 名男士，则租住一晚的住宿房费最少为 元
►考向五 图形面积问题
32．（2019·南京）某地计划对矩形广场进行扩建改造.如图，原广场长50m，宽40m，要求扩充后的矩形广场长与宽的比为3：2.扩充区域的扩建费用每平方米30元，扩建后在原广场和扩充区域都铺设地砖，铺设地砖费用每平方米100元.如果计划总费用642000元，扩充后广场的长和宽应分别是多少米？
33．（2023·常州）如图，在打印图片之前，为确定打印区域，需设置纸张大小和页边距（纸张的边线到打印区域的距离），上、下，左、右页边距分别为 SKIPIF 1 < 0 ．若纸张大小为 SKIPIF 1 < 0 ，考虑到整体的美观性，要求各页边距相等并使打印区域的面积占纸张的 SKIPIF 1 < 0 ，则需如何设置页边距？
34．（2023·淮安）为了便于劳动课程的开展，学校打算建一个矩形生态园 SKIPIF 1 < 0 （如图），生态园一面靠墙（墙足够长），另外三面用 SKIPIF 1 < 0 的篱笆围成．生态园的面积能否为 SKIPIF 1 < 0 ？如果能，请求出的长；如果不能，请说明理由．
35．（2023·大庆）如图1，在平行四边形中， SKIPIF 1 < 0 ，已知点在边上，以1m/s的速度从点向点运动，点 SKIPIF 1 < 0 在边 SKIPIF 1 < 0 上，以 SKIPIF 1 < 0 的速度从点向点 SKIPIF 1 < 0 运动．若点，同时出发，当点到达点时，点恰好到达点处，此时两点都停止运动．图2是 SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 与点的运动时间 SKIPIF 1 < 0 之间的函数关系图象（点 SKIPIF 1 < 0 为图象的最高点），则平行四边形的面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
36．（2023·海南）如图1，抛物线 SKIPIF 1 < 0 交x轴于A， SKIPIF 1 < 0 两点，交y轴于点 SKIPIF 1 < 0 ．点P是抛物线上一动点．
（1）求该抛物线的函数表达式；
（2）当点P的坐标为 SKIPIF 1 < 0 时，求四边形 SKIPIF 1 < 0 的面积；
（3）当动点P在直线上方时，在平面直角坐标系是否存在点Q，使得以B，C，P，Q为顶点的四边形是矩形？若存在，请求出点Q的坐标；若不存在，请说明理由；
（4）如图2，点D是抛物线的顶点，过点D作直线 SKIPIF 1 < 0 轴，交x轴于点H，当点P在第二象限时，作直线 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别与直线 SKIPIF 1 < 0 交于点G和点I，求证：点D是线段 SKIPIF 1 < 0 的中点．
37．（2023·淄博）如图，一条抛物线 SKIPIF 1 < 0 经过 SKIPIF 1 < 0 的三个顶点，其中 SKIPIF 1 < 0 为坐标原点，点 SKIPIF 1 < 0 ，点在第一象限内，对称轴是直线 SKIPIF 1 < 0 ，且的面积为18
（1）求该抛物线对应的函数表达式；
（2）求点的坐标；
（3）设为线段的中点，为直线 SKIPIF 1 < 0 上的一个动点，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 沿翻折，点的对应点为 SKIPIF 1 < 0 ．问是否存在点，使得以，，，为顶点的四边形是平行四边形？若存在，求出所有符合条件的点的坐标；若不存在，请说明理由．
中考解密（分析考察方向，精准把握重难点）
重点考向（以真题为例，探究中考命题方向）
►考向一 购买、分配类问题
►考向二 工程、行程类问题
►考向三 销售、利润类问题
►考向四 最优方案问题
►考向五 图形面积问题
购票人数 SKIPIF 1 < 0 （人）
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
每人门票价（元）
60
50
40
品名
甲蔬菜
乙蔬菜
批发价/（元/kg）
SKIPIF 1 < 0
SKIPIF 1 < 0
零售价/（元/kg）
SKIPIF 1 < 0
SKIPIF 1 < 0
阶梯
年用气量
销售价格
备注
第一阶梯
SKIPIF 1 < 0 SKIPIF 1 < 0 （含400）的部分
2.67元 SKIPIF 1 < 0
若家庭人口超过4人的，每增加1人，第一、二阶梯年用气量的上限分别增加 SKIPIF 1 < 0 .
第二阶梯
SKIPIF 1 < 0 （含1200）的部分
3.15元
第三阶梯
SKIPIF 1 < 0 以上的部分
3.63元



进价（元/件）
45
60
售价（元/件）
66
90
工程队
每天施工面积（单位：）
每天施工费用（单位：元）
甲
SKIPIF 1 < 0
3600
乙
x
2200
销售价格x（元/千克）
50
40
日销售量y（千克）
100
200
购买砂糖枯千克
SKIPIF 1 < 0
SKIPIF 1 < 0
用线下销售方式购买所需费用元
▲
▲
用线上销售方式购买所需费用元
▲
SKIPIF 1 < 0
▲
甲型客车
乙型客车
载客量人辆
SKIPIF 1 < 0
租金元辆
SKIPIF 1 < 0
SKIPIF 1 < 0