
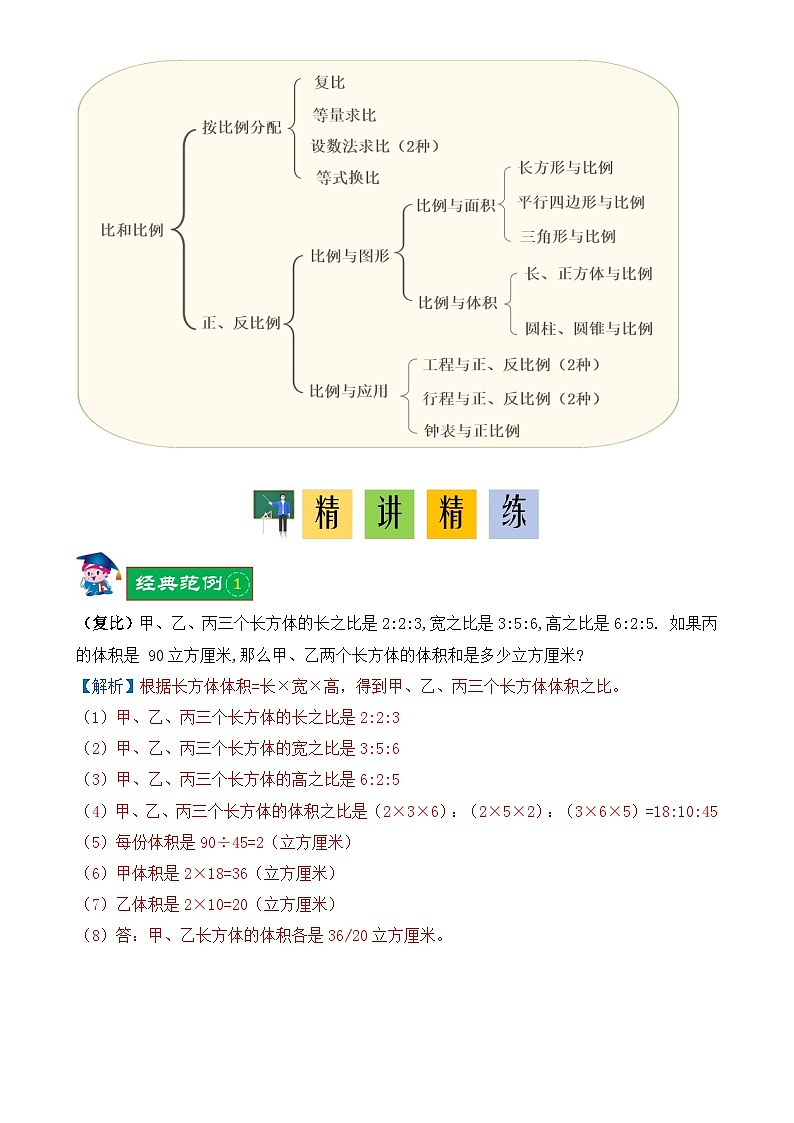
经典奥数-比和比例15种类型精讲精练-小升初奥数应用题讲义-A4
展开
这是一份经典奥数-比和比例15种类型精讲精练-小升初奥数应用题讲义-A4,共29页。试卷主要包含了按比例分配等内容,欢迎下载使用。
一、比
比是除法知识的拓展,是反映一道题中数量关系的常规形式,它与分数能够相互转化。运用比的知识处理分数、百分数和工程等问题时,可以化繁为简,使解题更加灵活方便。
求两个量之间的比时,关键要把握以下三点:
(1)分析题意,正确找出两种相关的量各是什么;
(2)弄清两种相关量对应的具体数量是多少,再按要求求比;
(3)当题目中没有直接告知具体量时,可以用假设、转换等方法确定两个量的份额或分率,最后求两个量的比。
二、按比例分配
将一个总量按一定的比分成若干个分量,叫作按比例分配。解题时,确定分配总量和分配的比是关键。一般包含和比、差比、单比三种类型。
解题一般步骤:
(1)找出或求出要分的总数;
(2)根据已知条件求总份数;
(3)按照要分配的各部分占总数的几分之几,分别求出每一部分是多少。
三、正、反比例
解题时,首先看题中是否含有不变量(定量),另外两个相关联的量一定要相互对应。
解题一般步骤:
(1)分析题意、找出题中两种相关联的量,判断它们是否成正比例关系或反比例关系。
(2)设未知数。
(3)根据正比例或反比例的意义列出比例。
(4)解比例。
(5)检验、作答。
(复比)甲、乙、丙三个长方体的长之比是2:2:3,宽之比是3:5:6,高之比是6:2:5. 如果丙的体积是 90立方厘米,那么甲、乙两个长方体的体积和是多少立方厘米?
【解析】根据长方体体积=长×宽×高,得到甲、乙、丙三个长方体体积之比。
(1)甲、乙、丙三个长方体的长之比是2:2:3
(2)甲、乙、丙三个长方体的宽之比是3:5:6
(3)甲、乙、丙三个长方体的高之比是6:2:5
(4)甲、乙、丙三个长方体的体积之比是(2×3×6):(2×5×2):(3×6×5)=18:10:45
(5)每份体积是90÷45=2(立方厘米)
(6)甲体积是2×18=36(立方厘米)
(7)乙体积是2×10=20(立方厘米)
(8)答:甲、乙长方体的体积各是36/20立方厘米。
某人买苹果和梨,苹果和梨的单价比是6:5,重量比是2:3,一共花去18元。求苹果和梨各花了多少钱。
(等量求比)两块一样重的铜锌合金,一块中铜与锌的比是2:5,另一块中铜与锌的比是1:3,现将两块合金熔成一块,求新的合金中铜与锌的比。
【解析】“两块合金重量相同”告诉我们可以将其转化为单位“1”相同的分率。
(1)两块合金中的铜各占其总量的22+5和11+3
(2)两块合金中的锌各占其总量的52+5和31+3
(3)新的合金中铜与锌的比是(22+5+11+3):(52+5+31+3)=15:41
(4)答:新的合金中铜与锌的比是15:41。
甲、乙两杯盐水,甲杯中的盐水是乙杯中的2倍,甲杯中盐和水的比是3:5,乙杯中盐与水的比是7:9,那么两杯盐水混合后盐与水的比是多少?
(设数法求比)如图所示,把一个正方体分割成A、B、C三个长方体,它们的表面积之比为3:4:5,求A、B、C三个长方体的体积之比。(巧妙设数解题)
【解析】如果设正方体的棱长是a的话,那么计算量非常大,此时巧妙设数很关键。
(1)设A、B、C表面积之和为3+4+5=12份
(2)A、B、C三个长方体的表面积由10个正方形面积组成。
(3)所以每个正方形面积是12÷10=1.2份,两个正方形面积为1.2×2=2.4份
(4)A、B、C三个长方体的高之比(即体积之比)=(3-2.4):(4-2.4):(5-2.4)
=0.6:1.6:2.6=3:8:13
(5)答:A、B、C三个长方体的体积之比是3:8:13.
一个长方形与一个正方形周长之比是6:5,长方形长是宽的75倍。求长方形与正方形的面积之比。
(连比)父亲将家里的 23 头牛分给三个儿子各自饲养,大儿子分得12,二儿子分得13,三儿子分得18。问:三个儿子各分得几头牛?
【解析】
(1)三个儿子的分配比为12:13:18=12:8:3
(2)12+8+13=23
(3)大儿子分得:23×1223=12(头)
二儿子分得:23×823=8(头)
三儿子分得:23×323=3(头)
(4)答:三个儿子个分得12、8、3头牛。
有一捆书,按照一年级得总数的12,二年级得总数的13,三年级得总数的17,正好是41本。问:各年级分别得多少本书?
(等式换比)甲、乙、丙三段木材一共长 24米,甲木材的25等于乙木材的12,且等于丙木材的23,求三段木材各是多长。
【解析】
(1)已知甲木材的25等于乙木材的12,且等于丙木材的23
(2)即甲×25=乙×12=丙×23
(3)设甲×25=乙×12=丙×23=1
(4)可求出甲:乙:丙=52:21:32=5:4:3
(5)5+4+3=12,24÷12=2(米)
(6)甲:2×5=10(米);乙:2×4=8(米);丙:2×3=6(米)
(7)答:甲、乙、丙三段木材的长度分别是10、8、6米。
有两支同样质地的蜡烛,但粗细、长短不同,一支能燃烧3.5小时,一支能燃烧5小当燃烧2小时的时候,两支蜡烛的长度恰好相同。问:这两支蜡烛的长度之比是多少?
(长方形与比例)一个长方形被分成 A、B、C、D四个小长方形,现知A的面积是2cm2,B的面积为4cm2,C的面积为6cm2。原长方形的面积是多少?
【解析】求原长方形面积,关键求出 D的面积,A、C的面积比与 B、D的面积比相等。
(1)因为长方形A与B宽相等,面积和长成正比例
(2)A与B的长之比为面积之比,即2:4=1:2(也等于C与D的长之比)
(3)长方形C与D的宽也相等,所以长方形C与D的面积与长成正比例
(4)长方形C与D的面积为1:2
(5)D的面积为6÷1×2=12(cm2)
(6)长方形面积为A+B+C+D=2+4+6+12=24 (cm2)
(7)答:原长方形的面积是24平方厘米。
或解:设D的面积为x平方厘米。
26=4x,解得x=12,所以长方形面积为2+4+6+12=24 (cm2)
如图1所示,长方形草地 ABCD 被分成面积相等的甲、乙、丙、丁四份,其中甲的长和宽比是a:b=2:1。那么乙的长和宽的比是多少?
(平行四边形与比例)如下图,平行四边形 ABCD 的两条高分别长14厘米、16厘米。如果平行四边形ABCD的周长是75厘米,它的面积是多少平方厘米?
【解析】平行四边形的面积一定,底与所对应的高成反比例
(1)因为BC×AE=CD×AF,则BC:CD=AF:AE=16:14=8:7
(2)BC+CD=75÷2=37.5cm
(3)BC=37.5÷(8+7)×8=20cm,CD=37.5-20=17.5cm
(4)平行四边形ABCD的面积是20×17.5=350(平方厘米)
(5)答:平行四边形的面积是350平方厘米。
如图,平行四边形ABCD中,AE垂直于BC,AF垂直于CD,AE=8cm,AF=7cm,AB+BC=45cm。平行四边形的面积是多少?
(三角形面积与比例)如下图1:阴影部分的面积是2平方厘米,AE=ED,BD=2DC,则△ABC的面积为多少?
【解析】高相等的三角形面积之比与底成正比例。
(1)连FD
(2)∵BD=2DC,三角形FBD的面积是三角形FDC面积的2倍
(3)设△DFC的面积是1份,则△BFD的面积是2份
(4)由AE=ED可以知道S△AEB=S△DEB;S△AEF=S△DEF
(5)∴S△AEB+ S△AEF =S△DEB+S△DEF,即S△ABF=S△BFD(阴影面积)
(5)S△ABF:S△BFD:S△DFC=2:2:1
(6)又∵阴影部分的面积是2平方厘米。S△ABC =2÷2×(2+2+1)=5(平方厘米)
(7)△ABC的面积为5平方厘米。
如图1,在△ABC中,CD=3BD,DE=EA。如果△ABC的面积是1,那么阴影部分的面积是多少?
(长、正方体与比例)已知一个长方体的长、宽、高的比是5:4:3,这个长方体所有棱长之和为240厘米,求这个长方体的体积。
【解析】长方体的棱长总和为240厘米,是长、宽、高之和的4倍,可以求出长、宽、高的和是240÷4=60厘米;又因为长、宽、高的比是5:4:3,将60厘米按5:4:3进行分配,就可以求出长方体的体积了。
(1)长+宽+高=240÷4=60(厘米)
(2)长方体的长、宽、高的比是5:4:3,共5+4+3=12份
(3)60÷12=5(厘米)
(4)长5×5=25(厘米),宽5×4=20(厘米),高5×3=15(厘米)
(5)长方体体积25×20×15=7500(立方厘米)
(6)答:这个长方体的体积是7500立方厘米。
已知一个长方体的棱长之和是264厘米,其中宽是长的23,高是宽的45。求这个长方体的体积。
(圆柱、圆锥与比例)一个圆柱和一个圆锥,底面半径比为2:3,高的比为4:9。则圆柱和圆锥的体积比是多少?(复比)
【解析】
(1)圆柱和圆锥的底面半径之比为2:3,则底面积之比为22:32=4:9
(2)高之比为4:9
(3)体积之比为(4×4):(3×9÷3)=16:9
现有甲、乙两个圆柱体容器,甲容器底面半径4厘米、高10厘米,盛有8.5厘米深的
水;乙容器底面半径3厘米、高10厘米。现在将甲容器中的部分水倒入乙容器,使甲、乙两容器的水深比为1:2。问:现在两个容器里各装有多少水?
(工程与正比例)生产一批零件,甲独做需20小时完成,乙每小时可做 30个。现在甲、乙两人同时合做,完成任务时,甲、乙生产零件数量之比为3:5,乙一共做了多少个?
【解析】关键求出乙的工作效率
(1)甲、乙同时合作,说明完成任务时间相同。时间一定,工作总量与工作效率成正比例
(2)甲、乙工作效率比是3:5
(2)(单比)乙每小时可做 30个,甲每小时可以做30÷5×3=18(个)
(3)甲独做20小时完成,工作总量为20×18=360(个)
(4)乙一共做了360÷(3+5)×5=225(个)
(5)综合列式:30÷5×3×20÷(3+5)×5=225(个),
(5)答:乙一共做了225个。
刘军、王强、李明三人合修一面墙,刘军、王强修6天修好围墙的13,王强,李明合修2天修好的余下的14,剩下的三人又合修5天才完成。他们一共得工资 1800 元,根据按劳分配的原则,每人应分多少钱?
(工程与反比例)如工一批零件,甲单独做需15天完成,乙单独需10 天完成。甲、乙两人合做这批零同时做完时,甲做了2400个,这批零件共多少个?
【解析】工作总量一定,此时甲、乙工作效率成反比例。
(1)甲、乙时间比为15:10=3:2
(2)甲、乙工效比为10:15=2:3
(3)甲、乙工作量比为10:15=2:3
(4)(单比)2400÷2×(2+3)=6000(个)
(5)答:这批零件共6000个。
某工厂生产一批产品,在完成了37后,引进新技术,效率提高了25%,结果比预计时间缩短了8天就完成。生产这批产品一共用了多少天?
(行程与正比例)从甲地到乙地,快车需6小时,慢车需要8小时。如果两车同时从甲、乙两地相对开出,可在距中点 35 千米处相遇。甲、乙两地距离是多少千米?(差比)
【解析】此题为中点相遇问题,先求出两车路程差,再用差比问题解决
(1)快车与慢车路程差(多行路程):35×2=70(千米)
(2)相遇时快车与慢车所用时间比6:8=3:4
(3)快车与慢车速度比为4:3
(4)时间一定,路程与速度成正比例。即快车与慢车相遇时所行的路程之比为4:3
(5)(差比)快车所行路程为70÷(4-3)×4=280(千米)慢车所行路程为70÷(4-3)×3=210(千米)
(6)全程为280+210=490(千米)
(7)详解:时间比6:8=3:4,速度比4:3
全程为35×2÷(4-3)×(4+3)=490(千米)
(8)答:甲、乙两地的距离是490千米。
1.甲、乙、丙三人进行百米赛跑。当甲到达终点时,乙距离终点5米,丙距离终点 10米。当乙到达终点时,丙距离终点多少米?
(行程与反比例)小明上坡每小时行3.6千米,下坡每小时行4.5千米。有个斜坡,小明先上坡再沿原路下坡,一共用1.8小时,这段斜坡长多少千米?
【解析】路程一定,速度和时间成反比例
(1)往返路程包含一个上坡和一个下坡两个全程
(2)上坡速度:下坡速度=3.6:4.5=4:5
(3)上坡时间:下坡时间=5:4(成反比例)
(4)上坡时间+上坡时间=1.8小时
(5)按比分配:上坡时间为1.8÷(5+4)×5=1(小时)
(6)全程1×3.6=3.6(千米)
或解:设上坡时间为x小时,则下坡时间为(1.8-x)小时。
列出方程为:3.6x=4.5(1.8-x),解得X=1
全程为1×3.6=3.6(千米)
答:这段斜坡长3.6千米。
甲车计划2小时从A地到B地。当甲在路上距B地还有160千米时,天下雨了,车速比原来了降低20%,结果比计划迟到20分钟。从A到B一共多少千米?
(钟表与正比例)有一只钟,每小时慢3分钟,早晨4点30分的时候,对准了标准时间,当钟指向当天上午 10点 50分的时候,标准时间是多少?
【解析】
(1)标准时间与坏钟时间之比为60:(60-3)
(2)坏种经过时间为10点50分-4点30分=6小时20分=380分钟
(3)用正比例方程解答
解:设钟的指向当天10点50分时,标准时间经过x分钟,则
X:380=60:(60-3)
解得:x=400
400-60=6小时40分
4点30分+6小时40分=11点10分
(4)答:标准时间为 11 点 10 分。
小明家有甲、乙两个闹钟,甲每小时慢2分钟,乙每小时快2分钟。在正午时候,小明把两个闹钟都调到12点整。当甲闹钟提示时刻为16点21分时,乙闹钟的时刻为多少?
(满分100分 测试时间:90分钟)
一、填空题(每题3分,共45分)
1.一种机械手表上的螺丝直径是4毫米,画在图纸上的长度是3.6厘米,则这张图纸的比例尺是 。
2.一个长方体框架,所有棱长的和是144厘米,长、宽、高的比是5:4:3,则这长方体框架的体积是 立方厘米。
3.小白兔和小黄兔各有胡萝卜数的比为3:4,若小黄免给小白兔4个胡萝卜,则它们的胡萝卜一样多,两只小兔共有 个胡萝卜。
4.把一根木料锯成4段要用12分钟,照这样,如果要锯成6段,一共需要 分钟。
5.甲、乙二人比赛爬楼梯,甲跑到第4层时,乙恰好跑到第3层,以这样的速度甲跑到第 28 层时,乙跑到第 层。
6.圆柱和圆锥底面周长比是2:3,体积比是8:5,圆柱与圆锥高的比是 。
7.一个两位数,十位上的数字比个位上的数字多5。若把它们调换位置,新得的两位数与原来两位数的比是3:8,则原来的两位数是 。
8.把三角形的一边减少20%,同时把这条边上的高增加20%,则新三角形的面积是原三角形面积的 %。
9.甲走的路程比乙多14,而乙走的时间比甲多15,甲、乙的速度比是 。
10.一个等腰三角形的两个角度数之比为2:5,它的顶角是 。
11.如图,长方形被两条直线分成四个小长方形,其中三个的面积分别是平方米、18平方米、30平方米,则图中阴影部分的长方形的面积为 平方米。
12.如图,一个正方形被分成四个四边形,它们的面积分别是110平方厘米、310平方厘米、15平方厘米、25平方厘米,若图中阴影部分是一个正方形,则阴影部分面积是平方厘米。
13. 如图,BD=2EB,且阴影部分的面积为42平方厘米。ABC的面积为 平方厘米。
14.如图,两个正方形中阴影部分面积比是3:1,空白部分的面积比是 。
15.如图,一个长方形被两条互相垂直的线段分割成甲丙、丁共4个小长方形,已知甲、乙、丁的面积分别是12、22、33,那么阴影三角形的面积是 。
二、应用题(每题5分,共55分)
16.某学生乘船由甲地顺流而下到乙地,然后又逆流而上到丙地,共用3小时,水流速度为2千米/时,船在静水中的速度为8千米/时。已知甲、丙两地间的距离为10千米,甲、乙两地间的距离为千米。
17.学校合唱队比舞蹈队多24人,合唱队人数的12等于舞蹈队人数的56。学校合唱队和舞蹈队各有多少人?
18.学校锅炉房里原来存有大、小两堆煤,共重48吨,现给小堆加上8吨,从大堆里用去14,两堆煤的重量正好相等,求大、小两堆煤原来各多少吨?
19.张家和李家本月收人钱数之比是8:5,本月开支的钱数之比是8:3,月底张家结余 240元,李家结余510元,则本月张家收入元。
20.在60米赛跑中,甲到终点时,乙还有10米,丙还有20米。按照这样的速度,Z到终点时,丙还有多少米?
21.甲、乙两种商品原价比是5:4,在搞促销期间,两种商品都降价30元,降价后甲、乙两种商品的价格比是9:7。求降价后甲、乙两种商品的价格各是多少元。
22.总路程是50千米,上坡、平路和下坡的路程比为1:2:3,行各段的时间比4:5:6,上坡速度是3千米/时求行完全程的时间。
23.甲、乙两人分别从A、B两地同时相向而行,到达对方出发地后都立即返回,两人第一次相遇点与第二次相遇点相隔9千米,甲与乙的速度比是3:2,求A、B两地间的距离。
24.买甲、乙两种铅笔共210支,甲种铅笔每支价钱3元,乙种铅笔每支价钱4元,两种铅笔用去的钱数相同。甲种铅笔买了多少支?
25.从甲地到乙地,A车需要行驶10 小时,B车需要行驶8小时。现在两车分别从甲、乙两地同时出发,相向而行,相遇时,A车离中点还有 30千米。甲、乙两地相距多少千米?
26.一项工程,用若干台同类型的机器可在规定的时间内完成。若增加2台机器,则只需规定时间的二就可以完成;若减少3台机器,则要推迟1小时才可以完成。那么10台机器去完成这项工程需要多少小时?
【能力冲浪】参考答案
某人买苹果和梨,苹果和梨的单价比是6:5,重量比是2:3,一共花去18元。求苹果和梨各花了多少钱。
【解析】根据总价=单价×数量,苹果总价:梨总价=(苹果单价×苹果数量):(梨单价×梨数量),即可求出苹果和梨的总价比。
(6×2):(5×3)=12:15=4:5
苹:18×49=8(元)梨:18×59=10(元)
答:苹果花了8元,梨花了10元。
甲、乙两杯盐水,甲杯中的盐水是乙杯中的2倍,甲杯中盐和水的比是3:5,乙杯中盐与水的比是7:9,那么两杯盐水混合后盐与水的比是多少?
【解析】把甲杯中盐与水的总份数变成乙杯中盐与水的总份数的2倍后,两个比的单位“1”就相同了。
(1)甲杯中盐和水的比是3:5=12:20
(2)乙杯中盐与水的比是7:9
(3)两杯盐水混合后盐与水的比是(7+12):(9+20)=19:29
(4)答:混合后盐与水的比是19:29.
一个长方形与一个正方形周长之比是6:5,长方形长是宽的75倍。求长方形与正方形的面积之比。
【解析】
(1)设长方形的周长为24,正方形的周长为20
(2)24÷2=12,长方形的长,12×75+7=7,宽是12×55+7=5,面积为7×5=35
(3)正方形边长为20÷4=5,面积为5×5=25
(4)长方形与正方形面积比是35:25=7:5
(5)答:长方形与正方形的面积之比是7:5.
有一捆书,按照一年级得总数的12,二年级得总数的13,三年级得总数的17,正好是41本。问:各年级分别得多少本书?
【解析】三个年级的分配比为12: 13:17,转换成整数比为21:14∶6,其份数和书本数正好对应。
(1)12: 13:17=21:14:6
(2)21+14+6=41
(3)一年级:41×2141=21(本)
二年级:41×1441=14(本)
三年级:41×641=6(本)
(4)答:一年级分得21本,二年级分得14本,三年级分得6本。
有两支同样质地的蜡烛,但粗细、长短不同,一支能燃烧3.5小时,一支能燃烧5小当燃烧2小时的时候,两支蜡烛的长度恰好相同。问:这两支蜡烛的长度之比是多少?
【解析】既然是求比,肯定不需要具体长度。
(1)设第一支长为a,第二支长为b
(2)则这两支蜡烛燃烧的速度分别是a3.5和b5,当燃烧 2小时后两支蜡烛长度相等
(3)此等量关系式可以写成a-a3.5×2=b-b5×2
(4)即57a=35b
(5)得到a:b=21:25
(6)答:这两支蜡烛的长度之比是21:25.
如图1所示,长方形草地 ABCD 被分成面积相等的甲、乙、丙、丁四份,其中甲的长和宽比是a:b=2:1。那么乙的长和宽的比是多少?
【解析】
(1)甲的长和宽比是a:b=2:1
(2)设甲的面积为2×1=2
(3)长方形草地的面积为2×4=8
(4)长方形草地的长AD=8÷a=8÷2=4
(5)把图1转化为图2,,则乙、丙、丁长宽都相等
(6)乙的长=AD-b=4-1=3,宽为2÷3=23
(7)乙的长与宽之比为3:23=9:2
(8)答:乙的长与宽之比为9:2
如图,平行四边形ABCD中,AE垂直于BC,AF垂直于CD,AE=8cm,AF=7cm,AB+BC=45cm。平行四边形的面积是多少?
【解析】平行四边形的面积一定,底与所对应的高成反比例
(1)因为BC×AE=CD×AF,则BC:CD=AF:AE=7:8
(2)BC+AB=45cm
(3)BC=45÷(8+7)×7=21cm
(4)平行四边形ABCD的面积是21×8=168(平方厘米)
(5)答:平行四边形的面积是168平方厘米。
如图1,在△ABC中,CD=3BD,DE=EA。如果△ABC的面积是1,那么阴影部分的面积是多少?
【解析】高相等的三角形面积之比与底成正比例。
(1)连FD
(2)∵CD=3BD,三角形FCD的面积是三角形FDB面积的3倍
(3)设△EDB的面积是1份,则△FDC的面积是3份
(4)由AE=ED可以知道S△AEF=S△DEF;S△AEC=S△DEC
(5)∴S△AEF+ S△AEC=S△DEF+S△DEC,即S△AFC=S△DFC(阴影面积)
(5)S△FBD:S△FDC:S△AFC=1:3:3
(6)又∵△ABC的面积是1,S△DFC =1÷(1+3+3)×2=27(平方厘米)
(7)阴影部分的面积为27平方厘米。
(8)答:阴影部分的面积为27平方厘米。
已知一个长方体的棱长之和是264厘米,其中宽是长的23,高是宽的45。求这个长方体的体积。
【解析】
(1)长方体的棱长总和为264厘米,是长、宽、高之和的4倍,所以长+宽+高的和是264÷4=66厘米
(2)长方体的长:宽=3:2=15:10
宽:高=5:4=10:8
(3)长:宽:高=15:10:8,15+10+8=33
(3)66÷33=2(厘米)
(4)长2×15=30(厘米),宽2×10=20(厘米),高2×8=16(厘米)
(5)长方体体积30×20×16=9600(立方厘米)
(6)答:这个长方体的体积是9600立方厘米。
现有甲、乙两个圆柱体容器,甲容器底面半径4厘米、高10厘米,盛有8.5厘米深的
水;乙容器底面半径3厘米、高10厘米。现在将甲容器中的部分水倒入乙容器,使甲、乙两容器的水深比为1:2。问:现在两个容器里各装有多少水?
【解析】先求出水的总体积,在求出甲、乙容器水量之比,最后按比例分配
(1)甲容器中水的体积为π×42×8.5=427.04(立方厘米)
(2)甲、乙容器中现在水深之比为1:2
(3)甲、乙容器的底面积之比为42:32=16:9
(4)现在甲、乙两个容器中水的体积之比为(1×16):(2×9)=8:9
(5)甲容器中现在水量为427.04÷(8+9)×8=200.96(立方厘米)
(6)乙容器中现在水量为427.04-200.96=226.08(立方厘米)
(7)答:甲、乙两个容器中个各装水200.96、226.08立方厘米。
刘军、王强、李明三人合修一面墙,刘军、王强修6天修好围墙的13,王强,李明合修2天修好的余下的14,剩下的三人又合修5天才完成。他们一共得工资 1800 元,根据按劳分配的原则,每人应分多少钱?
【解析】“按劳分配”即工资与工作量成正比。分别算出刘军、李强和王强的工效各是多少,再结合三人的工作时间分别求出每人的工作总量,进而求出三人工资。
(1)刘军、王强的工作效率之和为13÷6=118
(2)王强、李明的工作效率之和为(1-13)×14÷2=112
(3)刘军、王强、李明三人工作效率之和为(1-13)×(1-14)÷5=110
(4)李明的工作效率为110-118=245;工作时间为2+5=7(天);工作总量为245×7=1445;
分配工资为1800×1445=560(元)
(5)刘军的工作效率为110-112=160;工作时间为6+5=22(天);工作总量为160×11=1160;
分配工资为1800×1160=330(元)
(6)王强工资为1800-560-330=910(元)
(7)刘军、王强、李明三人各分得330元、910元、560元。
某工厂生产一批产品,在完成了37后,引进新技术,效率提高了25%,结果比预计时间缩短了8天就完成。生产这批产品一共用了多少天?
【解析】引进新技术后的工效和原来的工效比为5:4,则时间比是4:5,时间正好少用8天,可以求出原来后面的(1-37)所用的时间。
(1)原来工效:现在工效=1:(1+25%)=4:5
(2)原来时间:现在时间==5:4,时间相差8天
(3)原来完成这批产品时间为8÷(5-4)×5÷(1-37)=70(天)
(4)现在一共时间为70-8=62(天)
(5)答:生产这批产品一共用了62天。
1.甲、乙、丙三人进行百米赛跑。当甲到达终点时,乙距离终点5米,丙距离终点 10米。当乙到达终点时,丙距离终点多少米?
【解析】根据题目可知,乙跑95 米时,丙跑了 90 米。当乙再跑5米就可以到达终点时,丙能跑多少米?
解法一
(1)时间一定,路程与速度成正比例
(2)乙、丙二人速度比(100-5):(100-10)=19:18
(3)当乙到达终点100米处,丙行的路程为100÷19×18=941419(米)
(4)丙离终点距离为100-941419=5519(米)
解法二
设:当乙到达终点时,丙距离终点x米。
9590=100x ,解得x=941419,100-941419=5519(米)
答:丙距离终点5519米。
甲车计划2小时从A地到B地。当甲在路上距B地还有160千米时,天下雨了,车速比原来了降低20%,结果比计划迟到20分钟。从A到B一共多少千米?
【解析】下雨后的车速与原车速比为4:5,时间比为5:4,恰好比计划多用20分钟,可以求出走160千米的原计划时间,进一步可求出原计划的车速,再由计划的车速和时间就可以求出A、B两地之间的距离。
(1)原速与下雨后车速之比为1:(1-20%)=5:4
(2)在160千米这一段路程原来用时与现在用时之比为4:5(反比例)
(3)在160千米这一段路程原来用时为20÷60÷(5-4)×4=43(小时)
(4)原来速度为160÷43=120(千米/时)
(5)全程为120×2=240(千米)
(6)答:从A到B一共240千米。
小明家有甲、乙两个闹钟,甲每小时慢2分钟,乙每小时快2分钟。在正午时候,小明把两个闹钟都调到12点整。当甲闹钟提示时刻为16点21分时,乙闹钟的时刻为多少?
【解析】求出甲钟的时间与标准时间的比,乙钟的时间与标准时间的比。在根据三者的连比,求出甲钟与乙钟的时间比。
(1)甲闹钟:标准闹钟时钟:乙闹钟=(60-2):60:(60+2)=29:30:31
(2)16点21分-12点=261分钟
(3)261÷29×31=279(分钟)(单比)
(4)279分钟=4小时39分
(5)乙闹钟的时刻为16时39分。
(6)答:乙闹钟的时刻为16时39分。
【经典测试】参考答案
(满分100分 测试时间:90分钟)
一、填空题(每题3分,共45分)
1.一种机械手表上的螺丝直径是4毫米,画在图纸上的长度是3.6厘米,则这张图纸的比例尺是 。
【解析】比例尺=图上距离:实际距离
3.6厘米:4毫米=36:4=9:1
【答案】9:1
2.一个长方体框架,所有棱长的和是144厘米,长、宽、高的比是5:4:3,则这长方体框架的体积是 立方厘米。
【解析】和比问题
长+宽+高=144÷4=36(厘米)
5+4+3=12
36÷12=3(厘米)
长×宽×高=(3×5)×(3×4)×(3×3)=1620(立方厘米)
【答案】1620立方厘米
3.小白兔和小黄兔各有胡萝卜数的比为3:4,若小黄免给小白兔4个胡萝卜,则它们的胡萝卜一样多,两只小兔共有 个胡萝卜。
【解析】差比问题
小黄兔比小白兔多4×2=8(个)
共有8÷(4-3)×(4+3)=56(个)
【答案】56
4.把一根木料锯成4段要用12分钟,照这样,如果要锯成6段,一共需要 分钟。
【解析】锯木料时间与锯木料的次数成正比例
12÷(4-1)×(6-1)=20(分钟)
【答案】20
5.甲、乙二人比赛爬楼梯,甲跑到第4层时,乙恰好跑到第3层,以这样的速度甲跑到第 28 层时,乙跑到第 层。
【解析】时间一定,爬楼梯的层数与速度成正比例
速度比(4-1):(3-1)=3:2
(28-1)÷3×2+1=19(层)
【答案】19
6.圆柱和圆锥底面周长比是2:3,体积比是8:5,圆柱与圆锥高的比是 。
【解析】复比问题
底面积之比为22:32=4:9
体积之比为8:5
高之比为(8÷4):(5×3÷9)=6:5
【答案】6:5
7.一个两位数,十位上的数字比个位上的数字多5。若把它们调换位置,新得的两位数与原来两位数的比是3:8,则原来的两位数是 。
【解析】列比例式解答
解:设个位上数字为x,则十位上数字是(x+5)
[10x+(x+5)]:[10(x+5)+x]=3:8
解得x=2
两位数为10×(2+5)+2=72
【答案】72
8.把三角形的一边减少20%,同时把这条边上的高增加20%,则新三角形的面积是原三角形面积的 %。
【解析】设数法,设原来底和高都为1。
1×(1-20%)×(1+20%)÷1=96%
【答案】96
9.甲走的路程比乙多14,而乙走的时间比甲多15,甲、乙的速度比是 。
【解析】复比
甲、乙所行路程比5:4
时间比5:6
速度比(5÷5):(4÷6)=3:2
【答案】3:2
10.一个等腰三角形的两个角度数之比为2:5,它的顶角是 。
【解析】等腰三角形的三个角之比为2:2:5或2:5:5.(和比问题)
180÷(2+2+5)×5=100°或180÷(2+5+5)×2=40°
【答案】100°或40°
11.如图,长方形被两条直线分成四个小长方形,其中三个的面积分别是12平方米、18平方米、30平方米,则图中阴影部分的长方形的面积为 平方米。
【解析】正比例
12:30=18:x,解得x=45
【答案】45
12.如图,一个正方形被分成四个四边形,它们的面积分别是110平方厘米、310平方厘米、15平方厘米、25平方厘米,若图中阴影部分是一个正方形,则阴影部分面积是 平方厘米。
【解析】因为110+310+15+25=1(平方厘米)
正方形的边长为1厘米
15:110=2:1,310:25=3:4
阴影图形的边长为1×(22+1-33+4)=521(厘米)
面积为521×521=25441(平方厘米)
【答案】25441
13.如图,BD=2EB,且阴影部分的面积为42平方厘米。△ABC的面积为 平方厘米。
【解析】高一定,面积与底成正比例。(底高模型)
∵BD=2EB,∴DB:BE=2:1,所以阴影部分面积:△ABC=2:1
【答案】2:1
14. ★★如图,两个正方形中阴影部分面积比是3:1,空白部分的面积比是 。
【解析】高一定,面积与底成正比例。(底高模型)
∵S△BEC:S△ECG=3:1
∴BC:CG=3:1
∴大、小正方形的面积比为32:12=9:1
S△ECG=1÷2=0.5,S△BCE=0.5×3=1.5
∴大、小两块空白部分面积之比为(9-1.5):(1-0.5)=15:1
【答案】15:1
15.如图,一个长方形被两条互相垂直的线段分割成甲丙、丁共4个小长方形,已知甲、乙、丁的面积分别是12、22、33,那么阴影三角形的面积是 。
【解析】★★分割法,等积变换法。
如图2-3所示,阴影部分面积为(甲+乙+丁)÷2=(12+22+33)÷2=33.5
【答案】33.5
二、应用题(每题5分,共55分)
16. ★★★某学生乘船由甲地顺流而下到乙地,然后又逆流而上到丙地,共用3小时,水流速度为2千米/时,船在静水中的速度为8千米/时。已知甲、丙两地间的距离为10千米,甲、乙两地间的距离为多少千米?
【解析】顺水速度=2+8=10千米/时,逆流速度为8-2=6千米/时
解:设甲、乙两地相距x千米。
x10+x-106=3或x10+x+106=3
解得:x=5或17.5
【答案】5或17.5
17.学校合唱队比舞蹈队多24人,合唱队人数的12等于舞蹈队人数的56。学校合唱队和舞蹈队各有多少人?
【解析】等式换比
设合唱队人数×12=舞蹈队人数×56=1
合唱队:舞蹈队=(1÷12):(1÷56)=5:3(差比)
24÷(5-3)=12(人)
合唱队:12×5=60(人)
舞蹈队:12×3=36(人)
【答案】60、36
18.学校锅炉房里原来存有大、小两堆煤,共重48吨,现给小堆加上8吨,从大堆里用去14,两堆煤的重量正好相等,求大、小两堆煤原来各多少吨?
【解析】假设法或方程法
假设小堆加上8吨就相当于大堆煤的(1-14)=34=3:4(和比)
(48+8)÷(3+4)=8(吨)
大堆煤:8×4=32(吨)
小堆煤:48-32=16(吨)
【答案】32、16
19.张家和李家本月收人钱数之比是8:5,本月开支的钱数之比是8:3,月底张家结余 240元,李家结余510元,则本月张家收入多少元?
【解析】方程法
解:设张家和李家本月开支的钱数为8x:3x。则
(8x+240):(3x+510)=8:5
解得x=180
张家收入8x+240=8×180+240=1680(元)
【答案】1680
20.在60米赛跑中,甲到终点时,乙还有10米,丙还有20米。按照这样的速度,乙到终点时,丙还有多少米?
【解析】时间一定,路程和速度成正比例
解:设丙离终点还有x千米。
60:(60-x)=(60-10):(60-20)
解得x=12
【答案】12
21.甲、乙两种商品原价比是5:4,在搞促销期间,两种商品都降价30元,降价后甲、乙两种商品的价格比是9:7。求降价后甲、乙两种商品的价格各是多少元。
【解析】差不变
甲、乙两种商品相差:30÷(55-4-99-7)=60(元)
甲60÷(9-7)×9-30=240(元)
乙60÷(9-7)×7-30=180(元)
【答案】240元、180元
22.总路程是50千米,上坡、平路和下坡的路程比为1:2:3,行各段的时间比4:5:6,上坡速度是3千米/时,求行完全程的时间。
【解析】路程之比为上坡:平路:下坡=1:2:3(和比)
上坡路长50÷(1+2+3)=253(千米),上坡时间=253÷3=259(小时)
全程时间=259÷4×(4+5+6)=10512(小时)
【答案】10512小时
23.甲、乙两人分别从A、B两地同时相向而行,到达对方出发地后都立即返回,两人第一次相遇点与第二次相遇点相隔9千米,甲与乙的速度比是3:2,求A、B两地间的距离。
【解析】时间一定,速度和路程成正比例
第二次相遇时甲、乙两人共行了3个全程
第一次相遇点在全程的33+2处(距离甲地)
第二次相遇在在全程的23+2×3-1=15处(距离甲地)
两次相遇点相当于全程的33+2-15=25
全程=9÷25=22.5(千米)
24.买甲、乙两种铅笔共210支,甲种铅笔每支价钱3元,乙种铅笔每支价钱4元,两种铅笔用去的钱数相同。甲种铅笔买了多少支?
【解析】总价一点,单价和数量成反比例
单价之比=3:4
数量之比=4:3(和比)
210÷(4+3)=30(支)
甲种铅笔支数:30×4=120(支)
【答案】120支
25.从甲地到乙地,A车需要行驶10 小时,B车需要行驶8小时。现在两车分别从甲、乙两地同时出发,相向而行,相遇时,A车离中点还有 30千米。甲、乙两地相距多少千米?
【解析】中点相遇问题
时间一定,速度和路程成反比例
A、B速度之比为8:10=4:5
路程差为30×2=60(千米)(差比)
60÷(5-4)×(4+5)=540(千米)
【答案】540千米
26.一项工程,用若干台同类型的机器可在规定的时间内完成。若增加2台机器,则只需规定时间的910就可以完成;若减少3台机器,则要推迟1小时才可以完成。那么10台机器去完成这项工程需要多少小时?
【解析】工作总量一定,工作效率和工作时间成反比例
原来时间:现在时间=10:9
工作效率之比为9:10(工效差比)
原来工作机器台数=2÷(10-9)×9=18(台)
减少3台机器,则原来和现在工作效率之比为18:(18-3)=6:5
原来时间:现在时间=5:6(时间差比)
原来工作时间=1÷(6-5)×5=5(小时)
工作总量=5×18=90(台)
10台机器完成工作时间=90÷10=9(小时)
【答案】9小时
相关试卷
这是一份经典奥数-组合图形的相关计算9种类型精讲精练-小升初奥数应用题讲义-A4,共29页。试卷主要包含了平移、旋转、对称翻折法,等积变形法,重叠法,转换法,方程法,特殊求值法,整体减空白法,作辅助线法等内容,欢迎下载使用。
这是一份优惠问题--五年级小学奥数精讲精练,共4页。
这是一份小升初奥数经典试题(一) 含答案,共3页。










