浙江省台州市黄岩第二高级中学、城峰中学等多校2024-2025学年高二上学期期中联考数学试卷(含答案)

这是一份浙江省台州市黄岩第二高级中学、城峰中学等多校2024-2025学年高二上学期期中联考数学试卷(含答案)，共19页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．直线的倾斜角为( )
A.B.C.D.不存在
2．在长方体中,若,即向量在基底下的坐标为,则向量在基底下的坐标为( )
A.B.C.D.
3．已知双曲线的焦距为6,则该双曲线的渐近线方程为( )
A.B.C.D.
4．已知向量,是平面的两个不共线向量,非零向量是直线l的一个方向向量,则“,,三个向量共面”是“”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
5．已知P是直线上一动点,过点P作圆的两条切线,切点分别为A、B,则四边形PACB的外接圆的面积的最小值为( )
A.B.C.D.
6．椭圆的右焦点关于直线的对称点Q在椭圆上,则椭圆的离心率是( )
A.B.C.D.
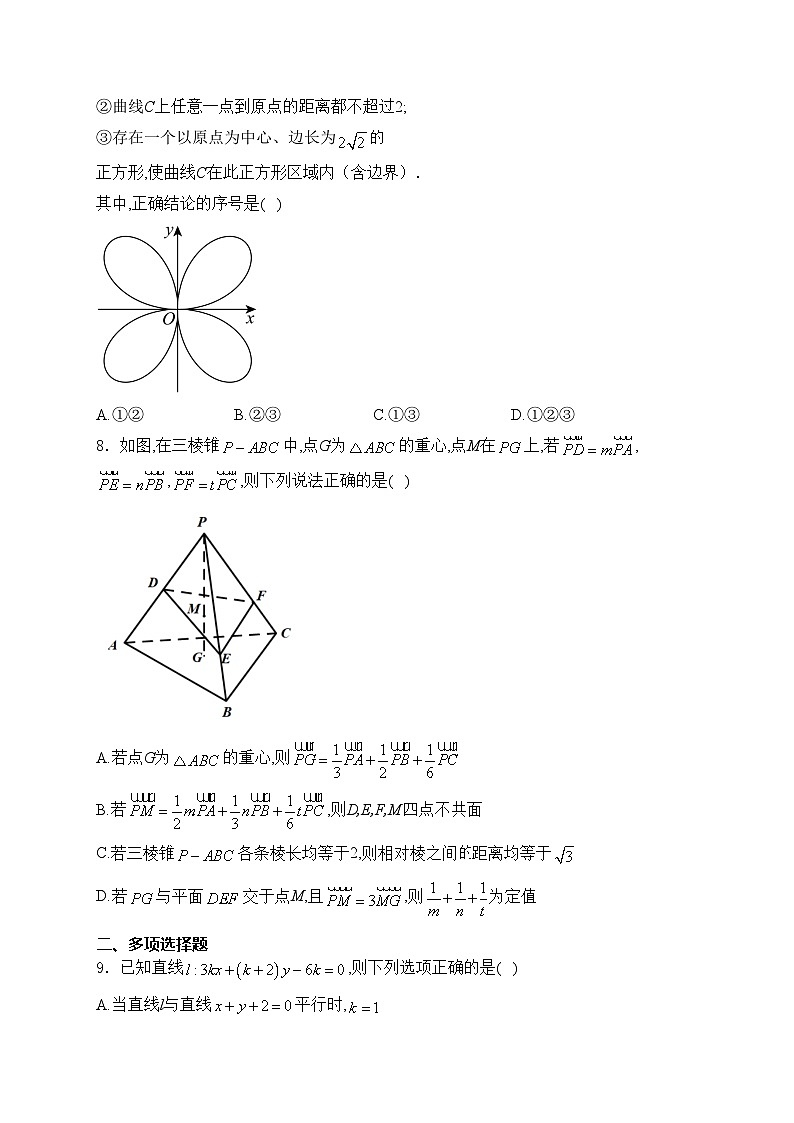
7．数学中有许多寓意美好的曲线,曲线被称为“四叶玫瑰线”（如图所示）．给出下列三个结论：
①曲线C关于直线对称;
②曲线C上任意一点到原点的距离都不超过2;
③存在一个以原点为中心、边长为正方形,使曲线C在此正方形区域内（含边界）．
其中,正确结论的序号是( )
A.①②B.②③C.①③D.①②③
8．如图,在三棱锥中,点G为的重心,点M在上,若,,,则下列说法正确的是( )
A.若点G为的重心,则
B.若,则D,E,F,M四点不共面
C.若三棱锥各条棱长均等于2,则相对棱之间距离均等于
D.若与平面交于点M,且,则为定值
二、多项选择题
9．已知直线,则下列选项正确的是( )
A.当直线l与直线平行时,
B.当直线l与直线垂直时,
C.当实数k变化时,直线,恒过点
D.原点到直线l的距离最大值为
10．如图,在正四棱柱中,,点P在线段上运动,则下列结论正确的是( )
A.三棱锥的体积为定值
B.若E为的中点,则直线平面
C.若点P运动到线段中点,则异面直线与所成角的正弦值是
D.直线与平面所成角的正弦的最大值为
11．已知点P是椭圆上的一点,O为坐标原点,椭圆的左、右焦点分别为,,下列选项正确的是( )
A.
B.若,且N是的中点,则
C.若的面积为1,则点P在第一象限的坐标为
D.若,则的最小值为1
三、填空题
12．已知方程表示焦点在y轴上的双曲线,则实数k的取值范围是__________．
13．已知,,且,,,则__________．
14．设O为坐标原点,,若上存在点P,使得,则r的取值范围是_____________．
四、解答题
15．已知,．
(1)若直线l过点,且点A,B到l的距离相等,求直线l的方程;
(2)在y轴上存在一点P,使得的值最小,求出点P的坐标．
16．已知圆过点,直线和均平分圆C．
(1)求圆的标准方程;
(2)过点P的直线l与圆C相交于M点,且,求直线l的一般式方程．
17．动点与定点的距离和它到定直线的距离的比是,动点的轨迹记为曲线C．
(1)求动点M的轨迹;
(2)已知直线与曲线C交于不同的两点A,B,且线段的中点在圆上,求实数m的值．
18．如图,在四棱锥中,平面平面ABCD,,,,,,E为中点,点F在上,且．
(1)求证：平面;
(2)求平面与平面夹角的余弦值;
(3)线段上是否存在点Q,使得平面,说明理由？
19．已知椭圆,若点,,,中恰有三点在椭圆C上．
(1)求C的方程;
(2)如图所示,记椭圆的左、右顶点分别为A,B,当动点M在定直线上运动时,直线,分别交椭圆于两点P,Q．
(ⅰ）证明：点B在以PQ为直径的圆内;
（ⅱ）求四边形面积的最大值．
参考答案
1．答案：C
解析：因为直线方程为：,与y轴平行,
所以直线倾斜角为,
故选：C.
2．答案：A
解析：因为,
所以向量在单位正交基底下的坐标为,
故选：A.
3．答案：B
解析：由已知双曲线的焦距,即,
所以,解得,
即双曲线方程为,
则其渐近线方程为,
故选：B.
4．答案：B
解析：当时,由于,是不共线的向量,故可用,作为基底表示出来,
即,,共面,所以“必要性”成立.
当,,共面时,直线l可能在平面内,故“充分性”不成立.
所以是必要不充分条件.
故选：B.
5．答案：D
解析：圆的方程,即为,圆心,
易知四边形PACB的外接圆的直径为PC,
PC的最小值为圆心C到直线的距离,即,
则四边形PACB的外接圆的半径为,
所以四边形PACB的外接圆的面积的最小值为.
故选：D.
6．答案：C
解析：设点Q的坐标为,因为F关于直线的对称点Q,
所以,即,解得,
所以点Q坐标是,
因为点Q在椭圆上,所以,得,
又,即,所以
所以该椭圆的离心率是.
故选：C.
7．答案：A
解析：对于①,设点是曲线上任一点,则有,
易得也成立,即点也在曲线C上,故曲线C关于直线对称,①正确;
对于②,不妨设点为曲线上的任一点,
则,化简得,当且仅当时取等号,
于是即得,故可得曲线C上任意一点到原点的距离都不超过2,故②正确;
对于③,联立,解得,
从而可得四个交点坐标分别为,,,,
依题意满足条件的最小正方形是各边以A,B,C,D为中点,边长为4的正方形（如图）,
故不存在一个以原点为中心、边长为的正方形,使曲线C在此正方形区域内（含边界）,即③错误.
故选：A.
8．答案：D
解析：对于A,连接并延长,交于点H,
由题意,可令作为空间向量的一组基底,
由,故A错误;
对于B,由,
则,
故,因此可得D,E,F,M四点共面,故B错误;
对于C,若三棱锥各条棱长均等于2,如图,将三棱锥放到正方体中,
由三棱锥的棱长为2,可得正方体的棱长为,
所以相对棱之间的距离即为正方体的棱长,等于,故C错误;
对于D,由,
连接,因为点D,E,F,M共面,所以存在唯一的实数对,
使,即,
所以．
由空间向量基本定理,知,,,
所以,则为定值,故D正确．
故选：D.
9．答案：AB
解析：对于A,直线的斜率为-1,直线l与直线平行,
所以直线l的斜率为-1,所以,故选项A正确;
对于B,直线l与直线垂直时,则,,
故选项B正确;
对于C,由,则,
则,所以,所以直线l过定点,
故选项C错误;
对于D,当且仅当原点到定点的距离为原点到直线l的距离时,
原点到直线l的距离最大,即,故选项D错误.
故选：AB.
10．答案：ACD
解析：对于A选项,在正四棱柱中,,且,
所以,四边形为平行四边形,所以,,
因为平面,平面,所以,平面,
因为,所以,点P到平面的距离等于点到平面的距离,
所以,为定值,A对;
对于B选项,以点D为坐标原点,、、所在直线分别为x、y、z轴建立如下图所示的空间直角坐标系,
设,则、、、、、,
因为E为的中点,则,则,,
所以,,所以,与不垂直,
故当E为的中点时,直线与平面不垂直,B错;
对于C选项,,,
则,
,
所以,,C对;
对于D选项,设平面的法向量为,,,
则,取,可得,此时,,
,
所以,
,
当且仅当时,等号成立,故直线与平面所成角的正弦的最大值为,D对.
故选：ACD.
11．答案：ABC
解析：对于A：易知,由椭圆方程可知：,,,
所以正确;
对于B：由椭圆的定义,,所以,又O,N分别为,的中点,
由中位线性质可知,正确;
对于C：设,,
由三角形面积可知：,解得：,
代入椭圆方程,解得：,故C正确;
D选项,因为,所以在椭圆内部,
又,所以,
所以,当P在线段上取等号,结合图象显然等号不成立,故错误;
故选：ABC.
12．答案：
解析：因为方程表示焦点在y轴上的双曲线,
则,解得.
故答案为：.
13．答案：
解析：因为,,,
所以,由,
所以,得,且,
所以,即,
得,所以.
故答案为：.
14．答案：
解析：设点,由,可知,
整理可得点P的轨迹方程为,,
即与存在交点,
易知,圆心距为,
因此,解得．
故答案为：.
15．答案：(1)和
(2)
解析：(1)当直线l过线段AB中点时,则线段AB的中点C的坐标为,
直线l过点,且点A,B到l的距离相等,
直线l的方程为,
当直线l与线段AB平行时,则,
得直线l的方程为：,即,
综上所知：所求的直线l的方程为和;
(2)点关于y轴对称的点为,则,
当且仅当,P,B三点共线时,的最小值为5.
由两点式可知,直线的方程为,
化简,得,当时,,
所以点P的坐标为.
16．答案：(1)
(2),
解析：(1)由点P在圆C上,则①,
又直线和均平分圆C,则直线和均过圆心C,
联立方程组,解得,
所以直线和的交点坐标为,即圆心C的坐标为2,1,
由圆可知,圆心C的坐标为,
则,解得,
将代入①,得,
所以圆C的方程为：,即,
故圆C的标准方程为：.
(2)由题可知,直线l的斜率存在,故设直线l的方程为,即,
取弦的中点为N,则,
由,且为等腰三角形,则,
又,则圆心到直线l的距离为,
由点到直线的距离公式可知：,解得,,
所以直线l的方程为,即直线l的一般式方程为：,.
17．答案：(1)M的轨迹是焦点在x轴上,实轴长为2、虚轴长为的双曲线
(2)
解析：(1)设d是点M到直线l的距离,则动点M的轨迹就是点的集合,
由此得,
两边平方,并化简,得,即,
即点M的轨迹是焦点在轴上,实轴长为2、虚轴长为的双曲线;
(2)设曲线C与直线的交点分别为,,
则,得,
,
,
线段的中点坐标为,
又线段的中点在圆上,
,解得.
18．答案：(1)证明见解析
(2)
(3)存在,理由见解析
解析：(1),,
,
,即
又,且,且两直线在平面内,
平面.
(2)平面平面,平面平面
,平面,
平面,又因为面,
.
由(1)已证,且已知,以A为原点,建立空间直角坐标系如图所示,
则,,,,,
,,,
E为PD的中点,
又,
设平面FAE的法向量为,则,
令,则,,
由(1)可知,平面,
平面的法向量为,
平面与平面夹角的余弦值为．
(3)线段上存在点Q,使得平面,
设,则
由(2)可知,平面的法向量,
则,
解得
当Q是中点时,则平面.
19．答案：(1)
(2)（ⅰ）证明见解析;（ⅱ）6
解析：(1)由椭圆对称性可知,,两点在椭圆上,
则,有一点在椭圆上,
设点在椭圆上,
则,方程组无解,所以点在椭圆上
代入,可得,,即椭圆方程为.
(2)（ⅰ）易知,,由椭圆对称性可知,
不妨设,,,,
根据题意可知直线AM,BM斜率均存在,且,,
所以直线AM的方程为,BM的方程为,
联立直线AM和椭圆方程,消去y可得,
由韦达定理可得,解得,则;
联立直线BM和椭圆方程,消去y可得,
由韦达定理可得,解得,则;
则,
,
所以,
即可知为钝角,以点B在以PQ为直径的圆内;
（ⅱ）由（i）四边形APBQ面积为
,
设,,则,当且仅当时等号成立,
由对勾函数性质可知在上单调递增,
所以,可得,
所以时,四边形的面积最大为6,此时点M的坐标为,
由对称性可知,即当点M的坐标为或时,四边形的面积最大,最大值为6．