河北省秦皇岛市青龙满族自治县青龙部分学校2025届高三上学期11月期中考试数学试卷(含答案)

这是一份河北省秦皇岛市青龙满族自治县青龙部分学校2025届高三上学期11月期中考试数学试卷(含答案)，共16页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．已知集合，则( )
A.B.C.D.
2．已知向量，，且满足，则( )
A.13B.C.26D.
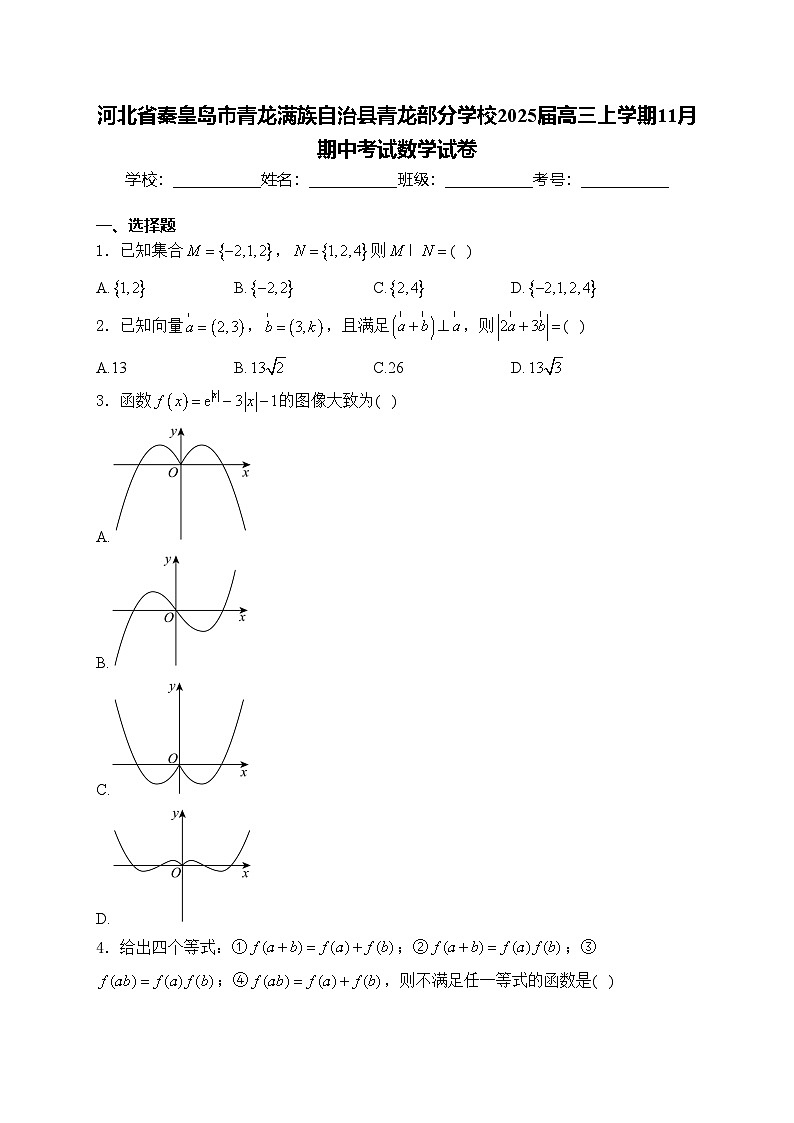
3．函数的图像大致为( )
A.
B.
C.
D.
4．给出四个等式：①；②；③；④，则不满足任一等式的函数是( )
A.B.C.D.
5．已知函数是定义在R上周期为3的奇函数，若，则( )
A.-1B.0C.1D.2016
6．不等式成立的充要条件是( )
A.B.C.D.
7．已知函数在R上单调递减，且关于x的方程恰好有两个不相等的实数解，则a的取值范围是( )
A.B.
C.D.
8．若，则的大小关系是( )
A.B.C.D.
二、多项选择题
9．已知，为复数，则下列说法正确的是( )
A.若，则
B.若，则与的虚部相等
C.若，则或
D.若，则
10．若的内角A，B，C对边分别是a，b，c，，且，则( )
A.外接圆的半径为B.的周长的最小值为
C.的面积的最大值为D.边的中线的最小值为
11．已知为常数，给出关于x的不等式，则( )
A.当，时，不等式的解集为
B.当时，不等式的解集为或的形式，其中
C.当时，不等式的解集为或的形式，其中，
D.当时，不等式的解集为的形式，其中
三、填空题
12．写出一个满足且不是常数函数的函数：_______.
13．中，若，，则_______.
14．已知向量，若，则_______.
四、解答题
15．设向量
(1)若求x的值；
(2)设函数求的最大值
16．在中，内角所对的边分别为，且满足.
(1)求的值；
(2)已知的面积为，求a的值.
17．将长为的铁丝截成12段，搭成一个正四棱柱的模型，以此为骨架做成一个容积最大的容器，则铁丝应怎样截？
18．已知函数.
(1)求函数的图像在点处的切线方程；
(2)求证：.
19．已知函数.
(1)若在定义域内恒成立，求a的取值范围；
(2)当a取(1)中的最大值时，求函数的最小值；
(3)证明不等式.
参考答案
1．答案：A
解析：根据集合的交集的计算得到：,
故选A
2．答案：B
解析：由题意得，∵，
∴，
即，解得
∴，
则，
故选：B
3．答案：C
解析：由函数的定义域为R，
且，
所以函数为偶函数，
当时，，则，
当时，；当时，，
所以在上单调递减，在上单调递增.
故选：C.
4．答案：D
解析：A项满足②；
B项满足④；
C项满足③；
D项不满足任一等式
故选D
5．答案：B
解析：因为，
所以，
所以，
又因为函数是定义在R上的周期为3的奇函数，
所以，
所以；
故选：B
6．答案：A
解析：，
故，
即，
故.
故选：A
7．答案：C
解析：由在上单调递减，得，
又由且在R上单调递减，
得，
解得，所以，
作出函数且在R上的大致图像，
由图像可知，在上，有且仅有一个解，
故在上，同样有且仅有一个解，
当，即时，
联立，即，
则，解得：，
当时，即，由图像可知，符合条件.
综上：.
故选：C
8．答案：B
解析：
，
故选：B
9．答案：AC
解析：对于A，若，则和互为共轭复数，所以，故A正确；
对于B，若，则与的虚部互为相反数，故B错误；
对于C，若，则，
所以或，可得或，故C正确；
对于D，取，，可得，故D错误.
故选：AC
10．答案：ACD
解析：对于A：，由正弦定理得，
即，
即，
因为，所以，
所以，，
因为，则，
令外接圆的半径为R,
根据正弦定理可得，
即，故A正确；
对于C：由余弦定理知，，
因为，，所以，，
当且仅当时等号成立，
因为，
所以的最大值为，故C正确；
对于B：由C知，则，
所以，
当且仅当时等号成立，
所以的最大值为，故B错；
对于D：因为为边上的中线，
所以，，
得，因为，
所以的最小值为，故D正确；
故选：ACD
11．答案：ACD
解析：当，时，，
即，解得，A正确；
设直线，联立，得，
由得或，直线与抛物线有两个交点；
由得或，直线与抛物线有一个交点；
由得，直线与抛物线无交点.
作出函数，，的图像，
当时，如图一，
由图可知，此时不等式解集为，B错误；
当时，如图二，由图可知，C正确；
当时，如图三，由图可知，D正确.
故选：ACD
12．答案：（答案不唯一）
解析：若，
则，
故符合题意的函数可以为.
故答案为：（答案不唯一，符合即可，其中且，其他满足条件的函数亦可）.
13．答案：
解析：由
得：.
将与分别平方作和得：
，
又
或
当时，，，，
，不合题意，.
故答案为：.
14．答案：
解析：因为，
所以，
因为，
所以，解得，
故答案为：
15．答案：(1)
(2)
解析:(1)由,
及,得.
又,从而,所以.
(2)
当时,
当时,
即时,取最大值1.
所以的最大值为.
16．答案：(1)2
(2)1或
解析：(1)由正弦定理得：,
，,
，
因为A，C是三角形内角，，
所以，
而由正弦定理得，
∴，即；
(2)由第一问可知，，设AB边上的高为h，
则三角形ABC的面积，
作下图：
过点C作AB的垂线，垂足为D，则，
设，则由勾股定理得到下列方程组：
，
解得，
由公式法得，
，；
17．答案：铁丝应截成12段等长的铁丝，正四棱柱模型的容积最大.
解析：设正四棱柱的底面边长为，
则该正四棱柱的高为，
由，可得，
则该正四棱柱的体积为，其中，
所以，，
当时，，此时函数单调递增，
当时，，此时函数单调递减，
故当时，函数取得最大值，
且，
故当铁丝应截成12段等长的铁丝，正四棱柱模型的容积最大.
18．答案：(1)
(2)证明见解析
解析：(1)因为，
所以，
所以，
又因为.
所以函数的图像在点处的切线方程为，
即.
(2)要证，
即证，
即证，
即证.
令，
则.
由，可得，（舍去）
因为当时，，
所以当时，，在上单调递减；
当时，，在上单调递增.
所以，
所以，结论得证.
另解：
证明：因为，
所以要证，即证，
即证.
设，
则.
令，
则，
而函数在上单调递减，
又，，
故存在唯一的，使得，
即，即，
等式两边同时取对数得，即.
当时，，在上单调递增；
当时，，在上单调递减.
所以，
即，
所以在上单调递减.
因为当时，，，
所以函数，所以成立.
19．答案：(1)
(2)
(3)证明见解析.
解析：(1)的定义域是，，
当时，，递减，
当时，，递增，
∴，依题意得，则；
(2)当时，，的定义域是，，
令，
由(1)知，的最小值是递增，
又，时，，
即递减，
当时，，
即递增，
∴；
(3)由(2)得，时，，
即，整理得，
又，则，令，
则，
即，
.