学年重庆市南川区三校联盟2024-2025学年上学期九年级期中数学试卷（A卷）

这是一份学年重庆市南川区三校联盟2024-2025学年上学期九年级期中数学试卷（A卷），共35页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（4分）下列四个数中，最小的数是（ ）
A．2B．C．﹣4D．0
2．（4分）下列图形是中心对称图形的是（ ）
A．B．
C．D．
3．（4分）反比例函数y＝经过点（﹣1，﹣4），则反比例函数的解析式为（ ）
A．y＝﹣4xB．y＝C．y＝﹣D．y＝4x
4．（4分）如图，将▱ABCD的一边BC延长至点E，若∠1＝65°（ ）
A．120°B．105°C．125°D．115°
5．（4分）如图，△ABC与△A'B'C'位似，点O为位似中心，AO＝3，则OA'的长度为（ ）
A．3B．6C．9D．12
6．（4分）估计的值应该在（ ）
A．7和8之间B．8和9之间
C．9和10之间D．10和11之间
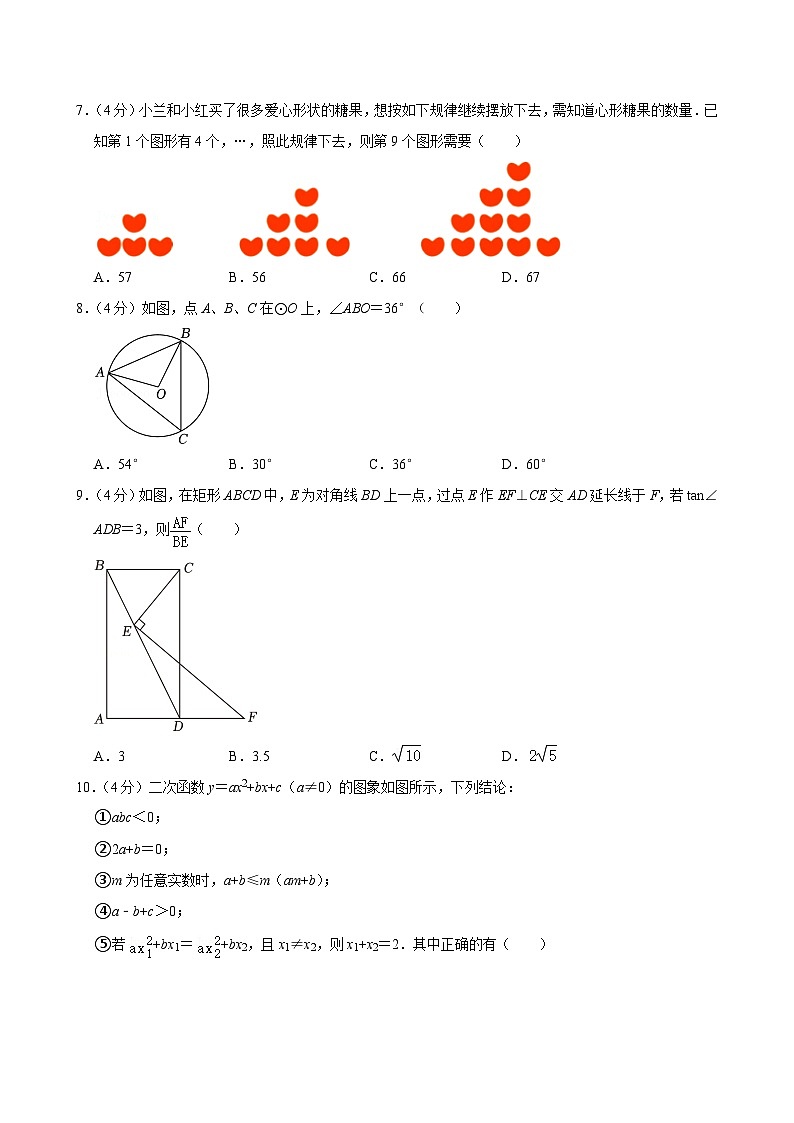
7．（4分）小兰和小红买了很多爱心形状的糖果，想按如下规律继续摆放下去，需知道心形糖果的数量．已知第1个图形有4个，…，照此规律下去，则第9个图形需要（ ）
A．57B．56C．66D．67
8．（4分）如图，点A、B、C在⊙O上，∠ABO＝36°（ ）
A．54°B．30°C．36°D．60°
9．（4分）如图，在矩形ABCD中，E为对角线BD上一点，过点E作EF⊥CE交AD延长线于F，若tan∠ADB＝3，则（ ）
A．3B．3.5C．D．
10．（4分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：
①abc＜0；
②2a+b＝0；
③m为任意实数时，a+b≤m（am+b）；
④a﹣b+c＞0；
⑤若+bx1＝+bx2，且x1≠x2，则x1+x2＝2．其中正确的有（ ）
A．1个B．2个C．3个D．4个
二、填空题：（本大题共8小题，每小题4分，共32分）将每小题的答案直接填写在答题卡中对应的横线上．
11．（4分）计算：（π﹣3）0﹣|﹣5|＝ ．
12．（4分）在桌面上放有四张背面完全一样的卡片，卡片正面分别标有数字﹣2，0，﹣1，随机抽取一张，记下数字后放回洗匀 ．
13．（4分）若正多边形的一个外角为30°，则这个多边形为正 边形．
14．（4分）为了响应“绿水青山就是金山银山”的倡导，某市2022年投入经费4000万元用于环境治理，2024年投入经费6000万元．设经费投入的年平均增长率为x ．
15．（4分）如图：在矩形ABCD中，对角线AC，BD交于点O，若圆弧与线段BC交于点E，且弧线恰好过点O，则图形中阴影部分的面积为 ．（结果保留π）
16．（4分）若关于x的一元一次不等式组的解集为x≥1，且关于y的分式方程，则所有满足条件的整数a的值之和是 ．
17．（4分）如图，在矩形ABCD中，AD＝8，对角线AC、BD相交于点E，将△ADE沿着DE翻折到△FDE，则CF的长为 ．
18．（4分）一个两位数M，若将十位数字2倍的平方与个位数字的平方的差记为数N，当N＞0时，N＝（2×4）2﹣72＝15＞0，则47的“叠加数”为4715；M＝26（2×2）2﹣62＝﹣20＜0，则26没有“叠加数”．那么34的“叠加数”是 ．若两位数M＝10a+b（1≤a≤5，1≤b≤4，且a、b均为整数）有“叠加数”，且12a﹣M﹣N能被13整除 ．
三、解答题：（本大题共8小题，第19题8分，其余各题10分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．
19．（8分）计算题：
（1）（m+1）（m﹣1）+m（3﹣m）．
（2）．
20．（10分）电信诈骗，严重危害着人民群众的财产安全．为提高大家的防范意识，南川区某校举行了主题为“防电信诈骗（百分制）进行整理描述和分析，成绩得分用x表示（80≤x＜85），B组（85≤x＜90），C组（90≤x＜95）（95≤x≤100），下面给出了部分信息：七年级10名学生的竞赛成绩：84，90，99，95，89，90，96，八年级10名学生的竞赛成绩在C组中的数据是：90，94，根据以上信息
七八年级抽取的学生竞赛成绩统计表
（1）上述图表中，a＝ ，b＝ ，m＝ ；
（2）根据以上数据，你认为七、八年级哪个年级掌握的相关知识较好？请说明理由（写出一条理由即可）；
（3）该校七年级有1600人，八年级有1000人参与此次竞赛，请估计该校七、八两个年级对防电信诈骗意识较强（x≥90）
21．（10分）如图，AC为矩形ABCD的对角线，AD＞AB．
（1）尺规作图：作AC的垂直平分线，垂足为点O，交AD于点E；（保留作图痕迹，不写作法）
（2）在（1）所作的图形中，连结AF，求证：四边形AFCE是菱形．（请补全下面的证明过程）
证明：∵四边形ABCD是矩形，
∴ ，
∴∠EAO＝∠FCO，∠AEO＝∠CFO．
∵EF平分AC，
∴ ，
∴△AOE≌ ，
∴AE＝ ，
又∵AE∥CF，
∴四边形AFCE是 ，
又∵EF⊥AC，
∴四边形AFCE是菱形．
22．（10分）为落实劳动教育，实施五育并举，某校合理利用空地，培养学生的劳动能力．农场去年春季种植蔬菜和水果共收获130kg．由于同学们劳动技能提高，今年春季蔬菜产量比去年增加10%，蔬菜和水果的总产量比去年增加18kg．
（1）去年春季蔬菜和水果的产量各多少千克？
（2）今年4月，收获劳动成果时，学校利用劳动课，两组同学同时开始劳动，结果水果采摘小组比蔬菜收割小组提前20分钟完成任务．问水果采摘小组每小时采摘水果多少千克？
23．（10分）如图，在矩形ABCD中，AB＝6，点E为CD的中点，动点P，点P以每秒1个单位长度沿折线E→D→A方向运动到点A停止，点Q也以每秒1个单位长度沿折线E→C→B方向运动到点B停止．设运动时间为x秒
（1）请直接写出y关于x的函数表达式并注明自变量x的取值范围；
（2）在给定的平面直角坐标系中画出这个函数的图象，并写出该函数的一条性质；
（3）若直线y1＝x+m与y的图象有且只有一个交点，请直接写出m的取值范围 ．
24．（10分）如图，码头A在码头B的正东方向，它们之间的距离为100海里．一货船由码头A出发，此时测得码头B在南偏西60°方向．
（1）那么码头A与小岛C距离；（结果保留根号）．
（2）货船在小岛C处准备返回码头B时发生故障，在原地等待救援，一艘救援船在码头A的正东方向和小岛C的南偏东60°方向D处以每小时60海里的速度沿射线DC方向前往进行救援，请通过计算说明救援船能否在补给船到达之前赶到小岛C．（参考数据：≈1.41，≈1.73，≈2.45 ）
25．（10分）如图，在平面直角坐标系中，抛物线y＝ax2+bx+4（a≠0）经过点，与x轴交于A，与y轴交于点C，抛物线的对称轴是直线x＝1．
（1）求抛物线的表达式；
（2）点P是直线BC上方抛物线上的一动点，过点P作PD∥y轴，交BC于点D．点M是y轴上的一动点，DM．当线段PD长度取得最大值时，求△PDM周长的最小值；
（3）将该抛物线进行平移，使得平移后的抛物线经过（2）中△PDM周长取得最小值时的点M（﹣4，0），F两点（E在F的左侧），连接EM．点N为平移后的抛物线上的一动点，请直接写出所有符合条件的点N的坐标．
26．（10分）如图，在等腰△ABC中，AB＝AC
（1）如图1，若∠BAC＝α，线段AD旋转到BA延长线上，交BC、AC于E，F，求∠AFD的度数（用含α的式子表示）；
（2）如图2，若∠BAC＝90°，线段AD绕点A旋转过程中，过点C作CE∥AB，连接DE，试用等式表示线段CD、AC、CE之间的数量关系，并说明理由；
（3）如图3，若∠BAC＝90°，，连接BD，交BD延长线DE于点E．当BE取最大值时，请直接写出
2024-2025学年重庆市南川区三校联盟九年级（上）期中数学试卷（A卷）
参考答案与试题解析
一、选择题：（本大题共10小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．
1．（4分）下列四个数中，最小的数是（ ）
A．2B．C．﹣4D．0
【分析】正数大于0，负数小于0．
【解答】解：∵，
∴四个数中最小的数是﹣2．
故选：C．
【点评】本题考查了有理数的大小比较，掌握正数大于0，负数小于0是解题的关键．
2．（4分）下列图形是中心对称图形的是（ ）
A．B．
C．D．
【分析】根据中心对称图形的概念判断即可．
【解答】解：选项A、C、D的图形都不能找到一个点，所以不是中心对称图形；
选项B的图形能找到一个点，使图形绕某一点旋转180度后与原来的图形重合．
故选：B．
【点评】本题考查的是中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后与原图重合．
3．（4分）反比例函数y＝经过点（﹣1，﹣4），则反比例函数的解析式为（ ）
A．y＝﹣4xB．y＝C．y＝﹣D．y＝4x
【分析】依据题意，将点（﹣1，﹣4）代入反比例函数解析式可以求得k的值，进而可以得解．
【解答】解：由题意，将点（﹣1，
∴﹣4＝．
∴k＝4．
∴反比例函数的解析式为y＝．
故选：B．
【点评】本题主要考查了待定系数法求反比例函数的解析式，解题时需要熟练掌握并理解．
4．（4分）如图，将▱ABCD的一边BC延长至点E，若∠1＝65°（ ）
A．120°B．105°C．125°D．115°
【分析】由∠1＝65°，求得∠BCD＝115°，由平行四边形的性质得∠A＝∠BCD＝115°，于是得到问题的答案．
【解答】解：∵∠1＝65°，
∴∠BCD＝180°﹣∠1＝180°﹣65°＝115°，
∵四边形ABCD是平行四边形，
∴∠A＝∠BCD＝115°，
故选：D．
【点评】此题重点考查平行四边形的性质，由∠1＝65°，求得∠BCD＝115°是解题的关键．
5．（4分）如图，△ABC与△A'B'C'位似，点O为位似中心，AO＝3，则OA'的长度为（ ）
A．3B．6C．9D．12
【分析】根据位似图形的概念得到△ABC∽△A'B'C'，AB∥A′B′，根据相似三角形的性质得到AB：A′B′＝1：4，证明△AOB∽△A'OB'，根据相似三角形的性质计算即可．
【解答】解：∵△ABC与△A'B'C'位似，
∴△ABC∽△A'B'C'，AB∥A′B′，
∵△ABC的周长等于△A'B'C'周长的，
∴AB：A′B′＝4：4，
∵AB∥A′B′，
∴△AOB∽△A'OB'，
∴OA：OA′＝AB：A′B′＝1：4，
∵AO＝3，
∴OA'＝12，
故选：D．
【点评】本题考查的是位似变换，掌握位似图形的概念、相似三角形的性质是解题的关键．
6．（4分）估计的值应该在（ ）
A．7和8之间B．8和9之间
C．9和10之间D．10和11之间
【分析】根据二次根式的混合运算的方法计算出结果为6+，先估算无理数，进而得到6+的大小即可．
【解答】解：＝6+，
∵＜＜，即1＜，
∴2＜6+＜8，
∴7＜＜4，
故选：A．
【点评】本题考查估算无理数的大小以及二次根式的混合运算，掌握算术平方根的定义以及二次根式混合运算的方法是正确解答的关键．
7．（4分）小兰和小红买了很多爱心形状的糖果，想按如下规律继续摆放下去，需知道心形糖果的数量．已知第1个图形有4个，…，照此规律下去，则第9个图形需要（ ）
A．57B．56C．66D．67
【分析】根据所给图形，依次求出所需爱心形状的糖果个数，发现规律即可解决问题．
【解答】解：由所给图形可知，
第1个图形需要的爱心形状的糖果个数为：4＝2+2+1；
第4个图形需要的爱心形状的糖果个数为：7＝1+4+3+1；
第6个图形需要的爱心形状的糖果个数为：11＝1+2+6+4+1；
…，
所以第n个图形需要的爱心形状的糖果个数为：2+2+3+…+n+6+1＝，
当n＝7时，
，
即第9个图形需要的爱心形状的糖果个数为56个．
故选：B．
【点评】本题主要考查了图形变化的规律，能根据所给图形发现所需爱心糖果个数的变化规律是解题的关键．
8．（4分）如图，点A、B、C在⊙O上，∠ABO＝36°（ ）
A．54°B．30°C．36°D．60°
【分析】根据等腰三角形的性质求出∠BAO的度数，由三角形内角和定理求出∠AOB的度数，再根据圆周角定理求出∠ACB的度数即可．
【解答】解：∵OA＝OB，
∴∠BAO＝∠ABO＝36°，
∴∠AOB＝180°﹣∠BAO﹣∠ABO＝180°﹣36°﹣36°＝108°，
∴ACB＝∠AOB＝．
故选：A．
【点评】本题考查圆周角定理，掌握等腰三角形的性质、三角形内角和定理、圆周角定理是解题的关键．
9．（4分）如图，在矩形ABCD中，E为对角线BD上一点，过点E作EF⊥CE交AD延长线于F，若tan∠ADB＝3，则（ ）
A．3B．3.5C．D．
【分析】过点E的PQ⊥AD于点Q，交BC于点P，则四边形ABPQ和四边形DCPQ都是矩形，设AQ＝BP＝m，DQ＝CP＝n，由＝tan∠PBE＝tan∠ADB＝＝3，得EP＝3BP＝3m，EQ＝3DQ＝3n，求得BE＝m，而∠FQE＝∠EPC＝∠CEF＝90°，则∠F＝∠PEC＝90°﹣∠QEF，所以△FQE∽△EPC，则＝＝3，所以FQ＝3EP＝9m，则AF＝10m，求得＝，于是得到问题的答案．
【解答】解：过点E的PQ⊥AD于点Q，交BC于点P，
∵四边形ABCD是矩形，
∴∠PQA＝∠A＝∠ABP＝90°，∠PQD＝∠CDQ＝∠DCP＝90°，
∴四边形ABPQ和四边形DCPQ都是矩形，∠PBE＝∠ADB，
∴∠BPE＝∠CPE＝90°，
设AQ＝BP＝m，DQ＝CP＝n，
∵＝tan∠PBE＝tan∠ADB＝，
∴EP＝3BP＝3m，EQ＝8DQ＝3n，
∴BE＝＝＝m，
∵EF⊥CE，
∴∠FQE＝∠EPC＝∠CEF＝90°，
∴∠F＝∠PEC＝90°﹣∠QEF，
∴△FQE∽△EPC，
∴＝＝＝3，
∴FQ＝7EP＝3×3m＝6m，
∴AF＝AQ+FQ＝m+9m＝10m，
∴＝＝，
故选：C．
【点评】此题重点考查矩形的判定与性质、相似三角形的判定与性质、解直角三角形等知识，正确地作出辅助线是解题的关键．
10．（4分）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：
①abc＜0；
②2a+b＝0；
③m为任意实数时，a+b≤m（am+b）；
④a﹣b+c＞0；
⑤若+bx1＝+bx2，且x1≠x2，则x1+x2＝2．其中正确的有（ ）
A．1个B．2个C．3个D．4个
【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
【解答】解：①抛物线开口方向向上，则a＞0．
抛物线对称轴位于y轴右侧，则a，即ab＜0．
抛物线与y轴交于y轴负半轴，则c＜3，
所以abc＜0．
故①错误；
②∵抛物线对称轴为直线x＝﹣＝5，
∴b＝﹣2a，即2a+b＝2，
故②正确；
③∵抛物线对称轴为直线x＝1，
∴函数的最小值为：a+b+c，
∴m为任意实数时，a+b≤m（am+b）2+bm+c，
故③正确；
④∵抛物线与x轴的一个交点在（5，0）的左侧，
∴抛物线与x轴的另一个交点在（﹣1，6）的右侧，
∴当x＝﹣1时，y＞0，
∴a﹣b+c＞6，
故④正确；
⑤∵+bx6＝+bx5，
∴+bx7﹣﹣bx3＝0，
∴a（x1+x3）（x1﹣x2）+b（x6﹣x2）＝0，
∴（x5﹣x2）[a（x1+x2）+b]＝0，
而x1≠x5，
∴a（x1+x2）+b＝4，即x1+x2＝﹣，
∵b＝﹣4a，
∴x1+x2＝8，
故⑤正确．
综上所述，正确的有②③④⑤．
故选：D．
【点评】主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．
二、填空题：（本大题共8小题，每小题4分，共32分）将每小题的答案直接填写在答题卡中对应的横线上．
11．（4分）计算：（π﹣3）0﹣|﹣5|＝ ﹣4 ．
【分析】先化简各式，然后再进行计算即可解答．
【解答】解：（π﹣3）0﹣|﹣6|＝ 1﹣5
＝﹣4，
故答案为：﹣4．
【点评】本题考查了零指数幂，绝对值，准确熟练地进行计算是解题的关键．
12．（4分）在桌面上放有四张背面完全一样的卡片，卡片正面分别标有数字﹣2，0，﹣1，随机抽取一张，记下数字后放回洗匀 ．
【分析】画树状图，共有16种等可能的结果，两次抽取卡片上的数字之积为负数的结果有4种，再由概率公式求解即可．
【解答】解：画树状图如图：
共有16种等可能的结果，两次抽取卡片上的数字之积为负数的结果有3种，
∴两次抽取卡片上的数字之积为负数的概率为＝，
故答案为：．
【点评】本题考查列表法与树状图法，概率公式，列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．解答本题的关键是熟练掌握概率的求法：概率＝所求情况数与总情况数之比．
13．（4分）若正多边形的一个外角为30°，则这个多边形为正 12 边形．
【分析】根据外角的度数就可求得多边形的边数．
【解答】解：正多边形的边数是：360÷30＝12．
故答案为：12．
【点评】本题主要考查了多边形的外角和定理，任何多边形的外角和都是360度．
14．（4分）为了响应“绿水青山就是金山银山”的倡导，某市2022年投入经费4000万元用于环境治理，2024年投入经费6000万元．设经费投入的年平均增长率为x 4000（1+x）2＝6000 ．
【分析】利用该市2024年投入用于环境治理的经费＝该市2022年投入用于环境治理的经费×（1+经费投入的年平均增长率）2，即可列出关于x的一元二次方程，此题得解．
【解答】解：根据题意得：4000（1+x）2＝6000．
故答案为：4000（2+x）2＝6000．
【点评】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
15．（4分）如图：在矩形ABCD中，对角线AC，BD交于点O，若圆弧与线段BC交于点E，且弧线恰好过点O，则图形中阴影部分的面积为 ．（结果保留π）
【分析】先证明△AOB是等边三角形，得到∠ABO＝60°，则∠EBO＝30°，再证明S△ABO＝S△BOC，则S阴影＝S扇形ABO﹣S△ABO+S△BOC﹣S扇形BOE＝S扇形ABO﹣S扇形BOE，由此求解即可．
【解答】解：∵四边形ABCD是矩形，
∴OA＝OB，∠ABC＝90°，
由作图方法可知AB＝OB，
∴OA＝OB＝AB，
∴△AOB是等边三角形，
∴∠ABO＝60°，
∴∠EBO＝30°，
∵四边形ABCD是矩形，
∴O是线段AC的中点，
∴S△ABO＝S△BOC，
∴S阴影＝S扇形ABO﹣S△ABO+S△BOC﹣S扇形BOE＝S扇形ABO﹣S扇形BOE＝＝．
故答案为：．
【点评】本题主要考查了矩形的性质，扇形面积，等边三角形的性质与判定，证明△AOB是等边三角形，得到∠ABO＝60°，∠EBO＝30°是解题的关键．
16．（4分）若关于x的一元一次不等式组的解集为x≥1，且关于y的分式方程，则所有满足条件的整数a的值之和是 ﹣14 ．
【分析】解不等式组，根据解集为x≥1求出a的取值范围；解分式方程，根据解题是正整数求出a的取值范围，从而确定满足条件的a的所有可能值，将它们相加即可．
【解答】解：解不等式组，得，
∵不等式组的解集为x≥1，
∴﹣≤1，
∴a≥﹣7；
解分式方程，得y＝，
∵y＝2是分式方程的增根，
∴≠2，
∴a≠﹣3，
∵分式方程的解是正数，
∴＞2，
∴a＜3，
∴﹣7≤a＜7且a≠﹣1，
∵分式方程的解是整数，
∴满足条件的整数a的值可能是﹣7，﹣2，1，
﹣7﹣2﹣3+1＝﹣14，
∴所有满足条件的整数a的值之和是﹣14．
故答案为：﹣14．
【点评】本题分式方程的解、解分式方程、解一元一次不等式组，掌握一元一次不等式组和分式方程的解法是解题的关键．
17．（4分）如图，在矩形ABCD中，AD＝8，对角线AC、BD相交于点E，将△ADE沿着DE翻折到△FDE，则CF的长为 ．
【分析】连接AF，交BD于点G，说明EG为△ACF的中位线，再利用勾股定理列方程即可解决问题．
【解答】解：连接AF，交BD于点G，
∵将△ADE沿着DE翻折到△FDE，
∴BD垂直平分AF，
∵四边形ABCD是矩形，
∴AE＝CE，AC＝BD，
∴EG是△ACF的中位线，
∴CF＝2EG，
在Rt△ABD中，由勾股定理得，
∴AE＝BE＝5，
设EG＝x，则BG＝5﹣x，
∴62﹣（2﹣x）2＝56﹣x2，
解得x＝，
∴CF＝2x＝，
故答案为：．
【点评】本题主要考查了翻折变换，矩形的性质，三角形中位线定理，勾股定理等知识，熟练掌握翻折的性质是解题的关键．
18．（4分）一个两位数M，若将十位数字2倍的平方与个位数字的平方的差记为数N，当N＞0时，N＝（2×4）2﹣72＝15＞0，则47的“叠加数”为4715；M＝26（2×2）2﹣62＝﹣20＜0，则26没有“叠加数”．那么34的“叠加数”是 3420 ．若两位数M＝10a+b（1≤a≤5，1≤b≤4，且a、b均为整数）有“叠加数”，且12a﹣M﹣N能被13整除 5484 ．
【分析】利用“叠加数”的定义，即可求出34的“叠加数”；由M＝10a+b，可得出N＝（2a）2﹣b2＝4a2﹣b2，将其代入12a﹣M﹣N中，可得出12a﹣M﹣N＝（2a﹣b）（1﹣2a﹣b），由12a﹣M﹣N能被13整除，可得出2a+b＝14，结合a，b的取值范围，可得出a，b的值，再利用“叠加数”的定义，即可求出结论．
【解答】解：∵M＝34，
∴N＝（2×3）6﹣42＝20，
∴34的“叠加数”是3420；
∵M＝10a+b，
∴N＝（8a）2﹣b2＝2a2﹣b2，
∴12a﹣M﹣N＝12a﹣（10a+b）﹣（5a2﹣b2）＝（4a﹣b）（1﹣2a﹣b）．
∵3≤a≤5，1≤b≤2，a，且12a﹣M﹣N能被13整除，
∴2a+b＝14，
∴，
∴M＝10a+b＝54，N＝4a2﹣b7＝4×58﹣42＝84，
∴满足条件的两位数M的“叠加数”为5484．
故答案为：3420，5484．
【点评】本题考查了二元一次方程的应用，由12a﹣M﹣N能被13整除，找出2a+b＝14是解题的关键．
三、解答题：（本大题共8小题，第19题8分，其余各题10分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．
19．（8分）计算题：
（1）（m+1）（m﹣1）+m（3﹣m）．
（2）．
【分析】（1）利用单项式乘多项式的法则，平方差公式进行计算，即可解答；
（2）先利用异分母分式加减法法则计算括号里，再算括号外，即可解答．
【解答】解：（1）（m+1）（m﹣1）+m（6﹣m）
＝m2﹣1+4m﹣m2
＝﹣1+3m；
（2）
＝•
＝•
＝•
＝
＝．
【点评】本题考查了整式的混合运算，分式的混合运算，单项式乘多项式，平方差公式，准确熟练地进行计算是解题的关键．
20．（10分）电信诈骗，严重危害着人民群众的财产安全．为提高大家的防范意识，南川区某校举行了主题为“防电信诈骗（百分制）进行整理描述和分析，成绩得分用x表示（80≤x＜85），B组（85≤x＜90），C组（90≤x＜95）（95≤x≤100），下面给出了部分信息：七年级10名学生的竞赛成绩：84，90，99，95，89，90，96，八年级10名学生的竞赛成绩在C组中的数据是：90，94，根据以上信息
七八年级抽取的学生竞赛成绩统计表
（1）上述图表中，a＝ 90 ，b＝ 94 ，m＝ 40 ；
（2）根据以上数据，你认为七、八年级哪个年级掌握的相关知识较好？请说明理由（写出一条理由即可）；
（3）该校七年级有1600人，八年级有1000人参与此次竞赛，请估计该校七、八两个年级对防电信诈骗意识较强（x≥90）
【分析】（1）根据扇形统计图可求出“C组”所占的百分比，即可求出m的值，根据中位数、众数的意义可求出a、b的值；
（2）通过中位数、平均数进行分析得出答案；
（3）利用七、八年级样本中的防电信诈骗意识较强（x≥90）的学生的占比分别乘以各对应的总人数，即可得到答案．
【解答】解：（1）七年级10名学生的竞赛成绩：84，90，99，100，90，96，
故众数a＝90，
∵八年级10名学生的竞赛成绩在C组中的数据是：90，94，
∴C组的百分比是，
∴m%＝1﹣20%﹣10%﹣30%＝40%，
∴m＝40，
根据各组占比可知，八年级10名学生的竞赛成绩的中位数是第从小到大排列后的第4个和第6个数据的平均数，即；
故答案为：90，94；
（2）八年级掌握的相关知识较好，理由如下：
∵两个年级的平均数均为91，但八年级的中位数94＞七年级的中位数90，
∴八年级掌握的相关知识较好；
（3）1600×+1000×，
答：该校七、八两个年级对防电信诈骗意识较强的学生一共有1660人．
【点评】本题考查频数（率）分布直方图，中位数，众数，方差，掌握平均数、中位数、众数的意义和计算方法是解答本题的关键．
21．（10分）如图，AC为矩形ABCD的对角线，AD＞AB．
（1）尺规作图：作AC的垂直平分线，垂足为点O，交AD于点E；（保留作图痕迹，不写作法）
（2）在（1）所作的图形中，连结AF，求证：四边形AFCE是菱形．（请补全下面的证明过程）
证明：∵四边形ABCD是矩形，
∴ AD∥BC ，
∴∠EAO＝∠FCO，∠AEO＝∠CFO．
∵EF平分AC，
∴ AO＝CO ，
∴△AOE≌ △COF（AAS） ，
∴AE＝ CF ，
又∵AE∥CF，
∴四边形AFCE是 平行四边形 ，
又∵EF⊥AC，
∴四边形AFCE是菱形．
【分析】（1）根据线段的垂直平分线的作法画图；
（2）根据菱形的判定定理证明．
【解答】解：（1）如图：EF即为所求；
（2）证明：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠EAO＝∠FCO，∠AEO＝∠CFO．
∵EF平分AC，
∴AO＝CO，
∴△AOE≌△COF（AAS），
∴AE＝CF，
又∵AE∥CF，
∴四边形AFCE是平行四边形，
又∵EF⊥AC，
∴四边形AFCE是菱形．
故答案为：AD∥BC，AO＝CO，CF．
【点评】本题考查了基本作图，掌握菱形的判定定理是解题的关键．
22．（10分）为落实劳动教育，实施五育并举，某校合理利用空地，培养学生的劳动能力．农场去年春季种植蔬菜和水果共收获130kg．由于同学们劳动技能提高，今年春季蔬菜产量比去年增加10%，蔬菜和水果的总产量比去年增加18kg．
（1）去年春季蔬菜和水果的产量各多少千克？
（2）今年4月，收获劳动成果时，学校利用劳动课，两组同学同时开始劳动，结果水果采摘小组比蔬菜收割小组提前20分钟完成任务．问水果采摘小组每小时采摘水果多少千克？
【分析】（1）设去年春季蔬菜的产量是x千克，水果的产量是y千克，则今年春季蔬菜的产量是（1+10%）x千克，水果的产量是（1+20%）y千克，根据去年春季及今年春季蔬菜和水果的总产量，可列出关于x，y的二元一次方程组，解之即可得出结论；
（2）设水果采摘小组每小时采摘水果m千克，则蔬菜收割小组每小时收割蔬菜1.2m千克，利用工作时间＝工作总量÷工作效率，结合水果采摘小组比蔬菜收割小组提前20分钟完成任务，可列出关于m的分式方程，解之经检验后，即可得出结论．
【解答】解：（1）设去年春季蔬菜的产量是x千克，水果的产量是y千克，水果的产量是（1+20%）y千克，
根据题意得：，
解得：．
答：去年春季蔬菜的产量是80千克，水果的产量是50千克；
（2）设水果采摘小组每小时采摘水果m千克，则蔬菜收割小组每小时收割蔬菜1.2m千克，
根据题意得：﹣＝，
解得：m＝40，
经检验，m＝40是所列方程的解．
答：水果采摘小组每小时采摘水果40千克．
【点评】本题考查了二元一次方程组的应用以及分式方程的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）找准等量关系，正确列出分式方程．
23．（10分）如图，在矩形ABCD中，AB＝6，点E为CD的中点，动点P，点P以每秒1个单位长度沿折线E→D→A方向运动到点A停止，点Q也以每秒1个单位长度沿折线E→C→B方向运动到点B停止．设运动时间为x秒
（1）请直接写出y关于x的函数表达式并注明自变量x的取值范围；
（2）在给定的平面直角坐标系中画出这个函数的图象，并写出该函数的一条性质；
（3）若直线y1＝x+m与y的图象有且只有一个交点，请直接写出m的取值范围 ﹣7≤m＜0或m＝9 ．
【分析】（1）直接确定三角形的底和高求解即可；
（2）描点、连线即可画出图象，再观察y的图象，可以从增减性写出函数的一条性质；
（3）先求得直线y1经过特殊点时的m的值，结合图象即可求解．
【解答】解：（1）当0≤x＜3时，y＝×4×2x＝8x；
当3≤x≤7时，y7＝AP•AB＝．
∴y关于x的函数关系式为y＝；
（2）画出函数图象如下，
函数y的一条性质：当0≤x＜2时，y随x的增大而增大，y随x的增大而减小；
（3）把（3，12）代入y1＝x+m得，12＝8+m，
把（7，0）代入y2＝x+m得，0＝7+m，
把（6，0）代入y1＝x+m得，7＝0+m，
∴若直线y1＝x+m与y的图象有且只有一个交点，请直接写出m的取值范围是﹣3≤m＜0或m＝9．
故答案为：﹣2≤m＜0或m＝9．
【点评】本题考查了一次函数的图象与系数的关系，一次函数图象上点的坐标特征，函数的图象和性质，正确求出函数解析式并画出图象，数形结合是解题的关键．
24．（10分）如图，码头A在码头B的正东方向，它们之间的距离为100海里．一货船由码头A出发，此时测得码头B在南偏西60°方向．
（1）那么码头A与小岛C距离；（结果保留根号）．
（2）货船在小岛C处准备返回码头B时发生故障，在原地等待救援，一艘救援船在码头A的正东方向和小岛C的南偏东60°方向D处以每小时60海里的速度沿射线DC方向前往进行救援，请通过计算说明救援船能否在补给船到达之前赶到小岛C．（参考数据：≈1.41，≈1.73，≈2.45 ）
【分析】（1）过C作CE⊥BA于E，根据三角函数的定义即可得到结论；
（2）根据等腰三角形的性质即可得到结论．
【解答】解：（1）过C作CE⊥BA于E，如图：
则∠CEB＝90°，
由题意得：∠BCE＝60°，∠CAE＝90°﹣45°＝45°，
∴△ACE是等腰直角三角形，
∴CE＝AE，AC＝，
设CE＝AE＝x海里，则AC＝，
在Rt△BCE中，tan∠BCE＝
∴BE＝CE＝，
∵BD＝AD+AB，
∴x＝x+100，
解得：x＝50+50，
∴x＝+50）＝50，
即AC＝（50+50，
答：码头A与小岛C距离为50+50；
（2）∵∠BCE＝∠DCE＝60°，
∴BC＝DC，
∵CE＝AE＝（50+50）海里，
∴CD＝6CE＝（100+100）海里，
∴救援船所用时间为≈8.55（小时）≈8.29（小时），
∵4.55＞4.29，
∴救援船不能在补给船到达之前赶到小岛C．
【点评】本题考查了解直角三角形的应用﹣方向角问题，正确作出辅助线构造直角三角形是解题的关键．
25．（10分）如图，在平面直角坐标系中，抛物线y＝ax2+bx+4（a≠0）经过点，与x轴交于A，与y轴交于点C，抛物线的对称轴是直线x＝1．
（1）求抛物线的表达式；
（2）点P是直线BC上方抛物线上的一动点，过点P作PD∥y轴，交BC于点D．点M是y轴上的一动点，DM．当线段PD长度取得最大值时，求△PDM周长的最小值；
（3）将该抛物线进行平移，使得平移后的抛物线经过（2）中△PDM周长取得最小值时的点M（﹣4，0），F两点（E在F的左侧），连接EM．点N为平移后的抛物线上的一动点，请直接写出所有符合条件的点N的坐标．
【分析】（1）利用待定系数法解答即可；
（2）利用抛物线的解析式求得点A，B，C的坐标，利用待定系数法求得直线BC的解析式，设P（m，+m+4），则D（m，﹣m+4），可得PD＝+m+4﹣（﹣m+4）＝+2m＝﹣+2，利用二次函数的性质求得PD的最大值为2；取点D关于y轴的对称点D′（﹣2，2），连接PD′，交y轴于点M，连接MD，由将军饮马模型可知此时PM+MD最小，MD＝MD′，再利用勾股定理解答即可得出结论；
（3）求得M的坐标，利用待定系数法求得平移后的抛物线的解析式，设N（P，﹣P+3），利用分类讨论的思想方法分两种情况讨论解答：①当点N在x轴上方时，连接EC，过点M作MH⊥EC于点H，过点N作NK⊥EF于点K，利用等腰直角三角形的判定与性质，直角三角形 的边角关系定理求得tan∠MEH＝，则tan∠NEF＝tan∠MEH＝，在Rt△NEK中利用直角三角形的边角关系定理列出关于p的方程解答即可；②当点N在x轴下方时，连接EC，过点M作MH⊥EC于点H，过点N作NR⊥EF于点R，利用①的方法解答即可．
【解答】解：（1）∵抛物线y＝ax2+bx+4（a≠3）经过点，对称轴是直线x＝1，
∴，
∴，
∴抛物线的表达式为y＝﹣+x+4；
（2）令y＝0，则﹣，
∴x＝﹣2或3，
∴A（﹣2，0），3）．
令x＝0，则y＝4，
∴C（7，4）．
设直线BC的解析式为y＝kx+n，
∴，
∴，
∴直线BC的解析式为y＝﹣x+4．
设P（m，+m+4），
∵PD∥y轴，
∴D（m，﹣m+3），
∴PD＝+m+4﹣（﹣m+4）＝+2，
∵＜0，
∴当m＝2时，PD取得最大值，5），2），
∴PD＝2，
取点D关于y轴的对称点D′（﹣5，2），交y轴于点M，如图，
∵点M是y轴上的一动点，
∴由将军饮马模型可知此时PM+MD最小，MD＝MD′，
∴PM+MD＝PM+MD′＝PD′．
∵DD′＝4，PD＝4，
∴PD′＝＝8，
∴△PDM周长的最小值＝2+2．
（3）设直线PD′的解析式为y＝cx+d，
∴，
∴，
∴直线PD′的解析式为y＝x+3，
令x＝2，则y＝3，
∴M（0，2）．
设平移后的抛物线的解析式为y＝﹣+ex+f，
∵平移后的抛物线经过（2）中△PDM周长取得最小值时的点M，且与x轴交于E（﹣4，
∴，
∴，
∴平移后的抛物线的解析式为y＝﹣﹣x+3．
设N（P，﹣P+3），
令y＝5，则﹣﹣，
∴x＝﹣3或．
∴F（，0）．
∵OE＝4，OM＝3，
∴EM＝＝5．
由（2）知：C（0，6）．
∴OC＝4，
∴CM＝1，OC＝OE＝5，
∴∠OEC＝∠OCE＝45°，EC＝4．
①当点N在x轴上方时，连接EC，过点N作NK⊥EF于点K，
则NK＝﹣P+3，
∴EK＝OE+OK＝p+8．
∵MH⊥EC，∠OCE＝45°，
∴CH＝HM＝，
∴EH＝，
∴tan∠MEH＝．
∵∠MEF+∠NEF＝45°，∠MEF+∠MEH＝45°，
∴∠NEF＝∠MEH，
∴tan∠NEF＝tan∠MEH＝，
∵tan∠NEF＝，
∴，
解得：p＝﹣4（不合题意，舍去）或p＝，
∴N（，）；
②当点N在x轴下方时，连接EC，过点N作NR⊥EF于点R，
则NR＝﹣（﹣P+3）＝，OR＝p，
∴ER＝OE+OR＝p+4．
∵MH⊥EC，∠OCE＝45°，
∴CH＝HM＝，
∴EH＝，
∴tan∠MEH＝．
∵∠MEF+∠NEF＝45°，∠MEF+∠MEH＝45°，
∴∠NEF＝∠MEH，
∴tan∠NEF＝tan∠MEH＝，
∵tan∠NEF＝，
∴，
解得：p＝﹣4（不合题意，舍去）或p＝，
∴N（，﹣）．
综上，所有符合条件的点N的坐标为（，﹣，）．
【点评】本题主要考查了二次函数的图象与性质，抛物线上点的坐标的特征，待定系数法，一次函数的图象与性质，一次函数图象上点的坐标的特征，轴对称的性质，将军饮马模型，直角三角形的性质，勾股定理，直角三角形的边角关系定理，等腰直角三角形的判定与性质，分类讨论的思想方法，利用点的坐标表示出相应线段的长度是解题的关键．
26．（10分）如图，在等腰△ABC中，AB＝AC
（1）如图1，若∠BAC＝α，线段AD旋转到BA延长线上，交BC、AC于E，F，求∠AFD的度数（用含α的式子表示）；
（2）如图2，若∠BAC＝90°，线段AD绕点A旋转过程中，过点C作CE∥AB，连接DE，试用等式表示线段CD、AC、CE之间的数量关系，并说明理由；
（3）如图3，若∠BAC＝90°，，连接BD，交BD延长线DE于点E．当BE取最大值时，请直接写出
【分析】（1）过点A作AH⊥BC于点H，利用等腰三角形的三线合一的性质和平行线的性质解答即可；
（2）过点A作AM⊥BC于点M，过点E作EN⊥BC，交BC的延长线于点N，利用等腰直角三角形的性质和全等三角形的判定与性质解答即可；
（3）由题意得：A，B，C，E四点在以BC为直径的圆上，可得：当AD⊥BD时，BE取得最大值；当AD⊥BD时，连接AE，EC，过点A作AF⊥AE，交BD于点F，利用等腰直角三角形的性质和全等三角形的判定与性质得到BF＝CE，
设AB＝3x，BF＝CE＝y，则AD＝FD＝ED＝x，AC＝AB＝3x，BE＝BF+FD+DE＝2x+y，利用等腰直角三角形的性质和勾股定理得到y与x的关系式，利用x的代数式表示出DE，BE，代入化简即可得出结论．
【解答】解（1）过点A作AH⊥BC于点H，如图，
∵AB＝AC，AH⊥BC，
∴∠BAH＝∠CAH＝∠BAC＝．
∵AH⊥BC，DE⊥BC，
∴AH∥DE，
∴∠AFD＝∠CAH＝α；
（2）线段CD、ACCD
过点A作AM⊥BC于点M，过点E作EN⊥BC，如图，
∵AB＝AC，∠BAC＝90°，
∴△ABC为等腰直角三角形，
∴∠ABC＝∠ACB＝45°，
∵AM⊥BC，
∴AMC为等腰直角三角形，
∴AM＝MC＝AC．
∵AD⊥DE，
∴∠ADM+∠EDN＝90°，
∵∠ADM+∠MAD＝90°，
∴∠MAD＝∠EDN．
在△MAD和△NDE中，
，
∴△MAD≌△NDE（AAS），
∴AM＝DN，
∴DN＝AC．
∵CE∥AB，
∴∠ECA＝∠BAC＝90°，
∵∠ACB＝45°，
∴∠ECN＝45°．
∵EN⊥BC，
∴△ECN为等腰直角三角形，
∴CN＝NE＝CE．
∵DN＝DC+CN，
∴DN＝DC+CE，
∴AC＝DC+，
∴AC＝CE+CD．
（3）＝．理由：
∵∠BAC＝90°，CE⊥BD，
∴∠E＝∠BAC＝90°，
∴A，B，C，E四点在以BC为直径的圆上，
由图形可知：当AD⊥BD时，BE取得最大值，
当AD⊥BD时，连接AE，过点A作AF⊥AE，如图，
∵AB＝AC，∠BAC＝90°，
∴∠ABC＝∠ACB＝45°，
∴∠E＝∠ACB＝45°，
∵AF⊥AE，
∴△AEF为等腰直角三角形，
∴AE＝AF，
∵AD⊥BD，
∴AD＝FD＝ED，
∵∠BAC＝∠FAE＝90°，
∴∠BAF＝∠EAC．
在△BAF和△CAE中，
，
∴△BAF≌△CAE（SAS），
∴BF＝CE，
设AB＝3x，BF＝CE＝y，
∴AC＝AB＝3x，BE＝BF+FD+DE＝6x+y，
∴BC＝AB＝3x．
∵BE2+EC2＝BC5，
∴，
∴y2+2xy﹣3x2＝0，
∴y＝（﹣4+2）x或y＝（﹣3﹣2，舍去），
∴BE＝6x+y＝（1+2）x．
∴＝．
【点评】本题主要考查了等腰三角形的性质，等腰直角三角形的性质，平行线的性质，全等三角形的判定与性质，圆的有关性质，直角三角形的性质，勾股定理，添加恰当的辅助线构造全等三角形是解题的关键年级
七年级
八年级
平均数
91
91
中位数
90
b
众数
a
100
方差
52
50.4
年级
七年级
八年级
平均数
91
91
中位数
90
b
众数
a
100
方差
52
50.4