江苏省宿迁市崇文初级中学2024—2025学年上学期八年级数学期中测试卷 (无答案)

这是一份江苏省宿迁市崇文初级中学2024—2025学年上学期八年级数学期中测试卷 (无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
试卷满分：150分 考试时间：120分钟
班级：___________ 姓名：___________
一、选择题（共8小题，每题3分，共24分）
1．下列四个选项中，不是的函数的是（ ▲ ）
A． B． C． D．
2．下列数据中不能确定物体位置的是（ ▲ ）
A．电影票上的“3排8号”B．小明住在某小区2栋105室
C．南偏西47°D．东经128°，北纬52°的城市
3．下列说法正确的是（ ▲ ）
A．4的平方根是B．8的立方根是
C． D．
4．在△中和△中，已知，，增加下列条件后还不能判定△≌△的是（ ▲ ）
A． B． C．D．
5．满足下列条件的△不是直角三角形的是（ ▲ ）
A．B．
C． D．
6．设面积为31的正方形的边长为，则的取值范围是（ ▲ ）
A． B． C．D．
7．平面直角坐标系中，为坐标原点，点的坐标为，将绕原点按逆时针方向旋转90°得，则点的坐标为（ ▲ ）
A． B． C．D．
8．在平面直角坐标系中，第四象限内的点到轴的距离是3，到轴的距离是2，平行于轴，，则点的坐标是（ ▲）
A．或 B．
C．D．或
二、填空题（共10小题，每小题3分，共30分）
9．函数中自变量的取值范围是 ▲ ．
10．用四舍五入法取近似值，将数0.01125精确到千分位的结果是 ▲ ．
11．已知图中的两个三角形全等，则 ▲ °．
12．已知函数是一次函数，则的值为 ▲ ．
13．已知和关于轴对称，则的值为 ▲ ．
14．若与是同一个数的两个不等的平方根，则这个数是 ▲ ．
15．如图，把一张△纸片沿折叠，若°，°，则的度数为 ▲ ．
16．如图，甲船从港口出发向东北方向航行16海里到达地，乙船同时从港口出发向东南方向航行12海里到达地，此时，两船之间的距离是 ▲ 海里．
17．如图，在△中，°，，在上取一点，延长到点，使得；在上取一点，延长到点，使得；…，按此做法进行下去，的度数为
▲ ．
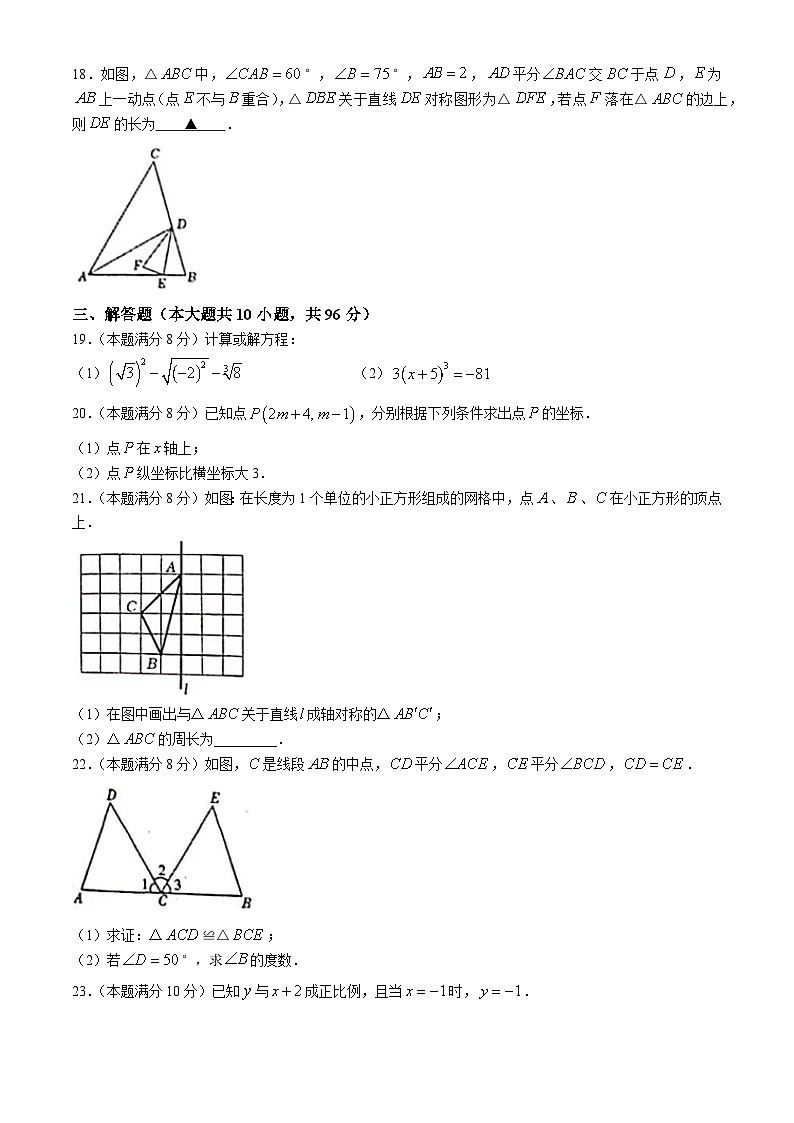
18．如图，△中，°，°，，平分交于点，为上一动点（点不与重合），△关于直线对称图形为△，若点落在△的边上，则的长为 ▲ ．
三、解答题（本大题共10小题，共96分）
19．（本题满分8分）计算或解方程：
（1）（2）
20．（本题满分8分）已知点，分别根据下列条件求出点的坐标．
（1）点在轴上；
（2）点纵坐标比横坐标大3．
21．（本题满分8分）如图：在长度为1个单位的小正方形组成的网格中，点、、在小正方形的顶点上．
（1）在图中画出与△关于直线成轴对称的△；
（2）△的周长为_________．
22．（本题满分8分）如图，是线段的中点，平分，平分，．
（1）求证：△≌△；
（2）若°，求的度数．
23．（本题满分10分）已知与成正比例，且当时，．
（1）求与之间的函数关系式；
（2）求当时的函数值；
（3）该函数图像与轴交于点，与轴交于点，求△的面积．
24．（本题满分10分）已知：如图，在四边形中，°，，．
（1）说明：；
（2）当于点时，试说明：．
25．（本题满分10分）如图，与相交于点，cm，点从点出发，沿→→方向以2cm/的速度运动，点同时从点出发，沿→方向以1cm/的速度运动，当点到达点时，、两点同时停止运动，设点的运动时间为．
（1）当点在→运动时，_________；（用含的代数式表示）
（2）求证：；
（3）当三点共线时，求的值．
26．（本题满分10分）由小学的学习知道：一组对边平行，另一组对边不平行的四边形为梯形，其中平行的一组对边称为底，不平行的一组对边称为腰，我们还将两腰相等的梯形称为等腰梯形，如图②，△≌△，连接、．
（1）当、、在一条直线上且°时，如图①．证明：四边形是等腰梯形；
（2）当、、不在一条直线上且°时，如图②．四边形还是等腰梯形吗？证明你的结论．
27．（本题满分12分）【问题背景】
著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为，较小的直角边长都为，斜边长都为，大正方形的面积可以表示为，也可以表示为，由此推导出重要的勾股定理：如果直角三角形两条直角边长为，斜边长为，则．
【探索求证】
（1）图②为美国第二十任总统伽菲尔德的“总统证法”，△与△按如图所示位置放置，连接，其中°，请你利用图②推导勾股定理；
【问题解决】
（2）如图③，在一条东西走向河流的一侧有一村庄，河边原有两个取水点，其中，由于某种原因，由到的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点（、、在同一条直线上），并新修一条路，且．测得千米，千米，求新路比原路少多少千米？
【延伸扩展】
（3）在第（2）向中若时，，设，求的值．
28．（本题满分12分）如图，°，，于点，于点．其中．
（1）求证：△≌△；
（2）若，求的长；
（3）连接，取的中点为，连接，判断△的形状，并说明理由．