天津市河北区2024－2025学年八年级上学期期中考试数学试卷

这是一份天津市河北区2024－2025学年八年级上学期期中考试数学试卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下列汽车标志中，不是轴对称图形的是（ ）
A．B．
C．D．
2．（3分）一个多边形的内角和是720°，这个多边形的边数是（ ）
A．4条B．5条C．6条D．7条
3．（3分）已知点M（3a+b，3）和点N（﹣2，a﹣2b）关于x轴对称，则a与b的值分别是（ ）
A．，B．，C．1，﹣1D．﹣1，1
4．（3分）如图，在△ABC中，AB＝AC＝8，BC＝5，BD为中线，则△ABD与△BCD的周长之差为（ ）
A．1B．2C．3D．4
5．（3分）如图所示，在△ABC中，∠BAC＝90°，AD⊥BC于点D，若∠B＝30°，BC＝8cm，则BD的长为（ ）
A．7cmB．6cmC．5.5cmD．5cm
6．（3分）如图，△ABC≌△DEC，AF⊥CD．若∠BCE＝65°，∠CAF的度数为（ ）
A．30°B．25°C．20°D．15°
7．（3分）根据下列条件，能画出唯一确定的三角形的是（ ）
A．AB＝2，BC＝5，AC＝2B．AB＝6，∠B＝30°，AC＝4
C．AB＝4，∠B＝60°，∠C＝75°D．BC＝8，∠C＝90°
8．（3分）如图，在△ABC中，已知BA＝BC，∠B＝120°，AB的垂直平分线DE交AC于点D．若AC＝6cm，则AD＝（ ）cm．
A．2B．3C．4D．2.8
9．（3分）如图，在△ABC中，分别以A，B为圆心，大于的长为半径作弧，两弧相交于D，E两点，分别以A，C为圆心，大于的长为半径作弧，两弧相交于F，G两点，且分别与BC相交于M，N两点，连接AM、AN，若∠MAN＝50°，则∠BAC＝（ ）
A．65°B．115°C．120°D．125°
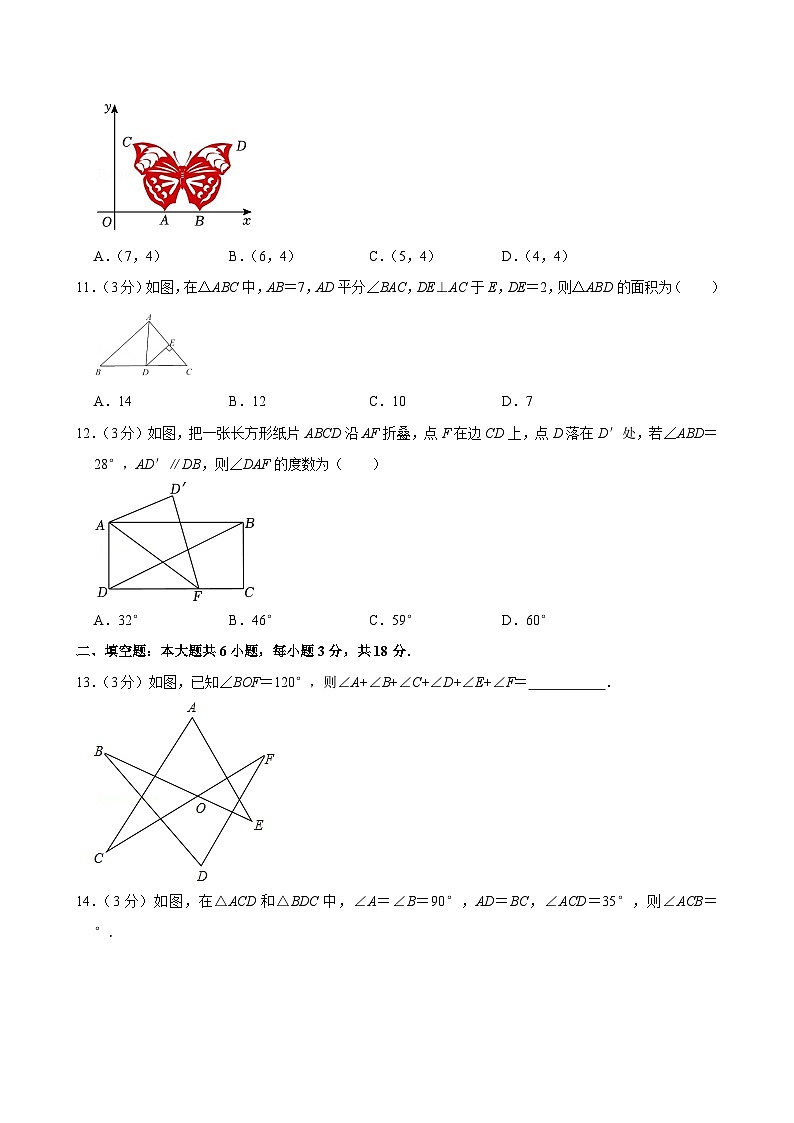
10．（3分）剪纸是中国古代最古老的民间艺术之一．如图是一张蕴含着轴对称变换的蝴蝶剪纸，点A与点B对称，点C与点D对称，将其放置在直角坐标系中，点A，B，C的坐标分别为（3，0），（5，0），（1，4），则点D的坐标为（ ）
A．（7，4）B．（6，4）C．（5，4）D．（4，4）
11．（3分）如图，在△ABC中，AB＝7，AD平分∠BAC，DE⊥AC于E，DE＝2，则△ABD的面积为（ ）
A．14B．12C．10D．7
12．（3分）如图，把一张长方形纸片ABCD沿AF折叠，点F在边CD上，点D落在D′处，若∠ABD＝28°，AD′∥DB，则∠DAF的度数为（ ）
A．32°B．46°C．59°D．60°
二、填空题：本大题共6小题，每小题3分，共18分．
13．（3分）如图，已知∠BOF＝120°，则∠A+∠B+∠C+∠D+∠E+∠F＝ ．
14．（3分）如图，在△ACD和△BDC中，∠A＝∠B＝90°，AD＝BC，∠ACD＝35°，则∠ACB＝ °．
15．（3分）三角形的三边长分别为5，1+2x，8，则x的取值范围是 ．
16．（3分）如图，在等边三角形ABC中，BC＝4，D是AB的中点，过点D作DF⊥AC于点F．过点F作FE⊥BC于点E，则EC的长为 ．
17．（3分）如图，在△ABC中，AF平分∠BAC，AC的垂直平分线交BC于点E，∠B＝70°，∠FAE＝19°，则∠C＝ 度．
18．（3分）如图，AD为∠CAF的角平分线，BD＝CD，过D作DE⊥AC于E，DF⊥AB交BA的延长线于F，则下列结论：①△CDE≌△BDF；②CE＝AB+AE；③∠BDC＝∠BAC；④∠DAF＝∠CBD．其中正确结论的序号有 ．
三、解答题：本大题共6小题，共46分，解答应写出文字说明，演算步骤或证明过程．
19．（6分）如图，在△ABC中，∠BAC＝56°，∠B＝43°，AD平分∠BAC，M是BC延长线上一点，过点M作MF⊥AD，垂足为H，MF分别与AB，AC交于点F，E．求∠M的度数．
20．（6分）如图，△ABC顶点坐标分别为A（1，4），B（﹣2，1），C（3，2）．将△ABC关于x轴对称△A′B′C′．
（1）请你画出△A′B′C′，并写出点A′，B′，C′的坐标；
（2）连接B′C，C′C，求△CB′C′的面积．
21．（8分）如图，在△ABC中，AD平分∠BAC，过线段CD上一点E作EG∥AD，交AC于点F，交BA的延长线于点G．
（1）求证：△AFG是等腰三角形．
（2）若CE＝EF，∠BAC＝80°，求∠B的度数．
22．（8分）如图，BE＝CF，DE⊥AB的延长线于点E，DF⊥AC于点F，且DB＝DC，
求证：AD是∠BAC的平分线．
23．（8分）如图，在△ABC中，∠A＝50°，DE垂直平分BC，∠ABC的角平分线BF交DE于△ABC内一点P，连接PC．若∠ACP＝28°，求∠ABP的度数．
24．（10分）如图所示，直线AB交x轴于点A（4，0），交y轴于点B（0，﹣4）．
（1）如图1，若点C的坐标为（﹣1，0），且AH⊥BC于点H，AH交OB于点P．求证：△OAP≌△OBC．
（2）如图2，若点D为AB的中点，点M为y轴正半轴上一动点，连接MD，过D作DN⊥DM交x轴于N点，当M点在y轴正半轴上运动的过程中，
①线段OM与AN有什么数量关系？
②若S表示三角形的面积，式子S△BDM﹣S△ADN的值是否发生改变？如发生改变，求出该式子的值的变化范围；若不改变，写出该式子的值．
2024-2025学年天津市河北区八年级（上）期中数学试卷
参考答案与试题解析
一、选择题：本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．（3分）下列汽车标志中，不是轴对称图形的是（ ）
A．B．
C．D．
【分析】根据轴对称图形的概念求解．
【解答】解：A、是轴对称图形，故错误；
B、是轴对称图形，故错误；
C、不是轴对称图形，故正确；
D、是轴对称图形，故错误．
故选：C．
【点评】本题考查了轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．
2．（3分）一个多边形的内角和是720°，这个多边形的边数是（ ）
A．4条B．5条C．6条D．7条
【分析】一个n边形的内角和为（n﹣2）•180°．所以多边形的内角和除以180°，所得的商加上2，就是多边形的边数．
【解答】解：720°÷180°+2
＝4+2
＝6（条），
所以，这个多边形的边数是6条．
故选：C．
【点评】本题主要考查多边形的内角和公式．解决问题的关键是理解：一个n边形的内角和为（n﹣2）•180°．
3．（3分）已知点M（3a+b，3）和点N（﹣2，a﹣2b）关于x轴对称，则a与b的值分别是（ ）
A．，B．，C．1，﹣1D．﹣1，1
【分析】关于x轴对称的点的横坐标相等，纵坐标互为相反数，由此可得，解方程即可．
【解答】解：∵点M（3a+b，3）和点N（﹣2，a﹣2b）关于x轴对称，
∴，
解得．
故选：D．
【点评】本题考查关于x轴、y轴对称的点的坐标、解二元一次方程组，熟练掌握关于x轴对称的点的坐标特征、二元一次方程组的解法是解答本题的关键．
4．（3分）如图，在△ABC中，AB＝AC＝8，BC＝5，BD为中线，则△ABD与△BCD的周长之差为（ ）
A．1B．2C．3D．4
【分析】先根据中线的定义得AD＝CD，再表示周长，即可得出答案．
【解答】解：∵BD是△ABC的中线，
∴AD＝CD．
∴△ABD与△BCD的周长之差是AB+AD+BD﹣（BC+BD+CD）＝AB﹣BC＝8﹣5＝3．
故选：C．
【点评】本题主要考查了三角形的中线，三角形的周长，掌握其性质是解决此题的关键．
5．（3分）如图所示，在△ABC中，∠BAC＝90°，AD⊥BC于点D，若∠B＝30°，BC＝8cm，则BD的长为（ ）
A．7cmB．6cmC．5.5cmD．5cm
【分析】求出∠DAC＝30°，利用含30°的直角三角形的性质求出CD＝2，则BD可求出．
【解答】解：∵∠BAC＝90°，∠B＝30°，
∴∠C＝90°﹣∠B＝60°，
∵AD⊥BC于点D，∠C＝60°，
∴∠DAC＝30°，
∴在Rt△ABC中，，
∴Rt△ACD中，∠DAC＝30°，
∴，
∴BD＝BC﹣CD＝8﹣2＝6（cm）．
故选：B．
【点评】此题主要考查含30度角的直角三角形，利用含30°的直角三角形的性质求出CD的长是解题的关键．
6．（3分）如图，△ABC≌△DEC，AF⊥CD．若∠BCE＝65°，∠CAF的度数为（ ）
A．30°B．25°C．20°D．15°
【分析】由全等三角形的性质可得∠ACB＝∠DCE，即可得∠BCE＝∠DCA，得到∠ACF＝65°，再根据直角三角形的性质即可求解．
【解答】解：∵△ABC≌△DEC，
∴∠ACB＝∠DCE，
∴∠ACB﹣∠ACE＝∠DCE﹣∠ACE，
即∠BCE＝∠DCA，
∵∠BCE＝65°，
∴∠DCA＝65°，
即∠ACF＝65°，
∵AF⊥CD，
∴∠AFC＝90°，
∴∠CAF＝90°﹣65°＝25°，
故选：B．
【点评】本题考查了全等三角形的判定和性质，垂直的定义，直角三角形的性质，掌握全等三角形的性质是解题的关键．
7．（3分）根据下列条件，能画出唯一确定的三角形的是（ ）
A．AB＝2，BC＝5，AC＝2B．AB＝6，∠B＝30°，AC＝4
C．AB＝4，∠B＝60°，∠C＝75°D．BC＝8，∠C＝90°
【分析】根据全等三角形的判定方法，逐一判断即可解答．
【解答】解：A、∵2+2＜5，即AB+AC＜BC，
∴此时三条线段不能构成三角形，不符合题意；
B、AB＝6，∠B＝30°，AC＝4，根据边边角不能确定唯一三角形，不符合题意；
C、AB＝4，∠B＝60°，∠C＝75°，根据角角边可以确定唯一三角形，符合题意；
D、BC＝8，∠C＝90°，只有一角和一边，不能确定唯一三角形，不符合题意；
故选：C．
【点评】本题考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解题的关键．
8．（3分）如图，在△ABC中，已知BA＝BC，∠B＝120°，AB的垂直平分线DE交AC于点D．若AC＝6cm，则AD＝（ ）cm．
A．2B．3C．4D．2.8
【分析】连接BD，根据线段垂直平分线的性质知△ABD是等腰三角形；然后证明△CDB是直角三角形，利用30度角所对的直角边是斜边的一半即可求得BD与CD间的数量关系，最后通过等量代换即可求得AC＝3AD，从而求得线段AD的长度．
【解答】解：连接BD，
∵AB的垂直平分线DE交AC于点D，
∴AD＝BD，
∴∠A＝∠ABD，
∵BA＝BC，∠B＝120°，
∴∠A＝∠C＝×（180°﹣120°）＝30°，
∴∠ABD＝30°，
∴∠CBD＝90°，
∴CD＝2BD，
∴CD＝2AD，
∴AC＝AD+CD＝AD+2AD＝3AD，
∵AC＝6cm，
∴AD＝2cm．
故选：A．
【点评】本题考查线段垂直平分线的性质、等腰三角形的性质、含30度角的直角三角形．利用含30度角的直角三角形的性质得出CD＝2BD是解题的关键．
9．（3分）如图，在△ABC中，分别以A，B为圆心，大于的长为半径作弧，两弧相交于D，E两点，分别以A，C为圆心，大于的长为半径作弧，两弧相交于F，G两点，且分别与BC相交于M，N两点，连接AM、AN，若∠MAN＝50°，则∠BAC＝（ ）
A．65°B．115°C．120°D．125°
【分析】由作图可知，直线DE为线段AB的垂直平分线，直线FG为线段AC的垂直平分线，则AM＝BM，AN＝CN，可得∠B＝∠BAM，∠C＝∠CAN，进而可得∠B+∠C＝65°，从而可得答案．
【解答】解：由作图可知，直线DE为线段AB的垂直平分线，直线FG为线段AC的垂直平分线，
∴AM＝BM，AN＝CN，
∴∠B＝∠BAM，∠C＝∠CAN．
∵∠B+∠BAC+∠C＝180°，
∴∠B+∠BAM+∠MAN+∠CAN+∠C＝2∠B+∠MAN+2∠C＝2（∠B+∠C）+50°＝180°，
∴∠B+∠C＝65°，
∴∠BAC＝180°﹣65°＝115°．
故选：B．
【点评】本题考查作图—基本作图、线段垂直平分线的性质，熟练掌握线段垂直平分线的性质是解答本题的关键．
10．（3分）剪纸是中国古代最古老的民间艺术之一．如图是一张蕴含着轴对称变换的蝴蝶剪纸，点A与点B对称，点C与点D对称，将其放置在直角坐标系中，点A，B，C的坐标分别为（3，0），（5，0），（1，4），则点D的坐标为（ ）
A．（7，4）B．（6，4）C．（5，4）D．（4，4）
【分析】由点A与点B对称，求得对称轴为x＝4直线，再根据点C与点D对称，即可求解．
【解答】解：∵A（3，0）和B（5，0）对称，
∴对称轴直线为：，
∵C（1，4）与点D关于x＝4对称，
∴D（7，4），
故选：A．
【点评】本题考查了坐标与图形变化﹣对称，熟知轴对称的性质是解题的关键．
11．（3分）如图，在△ABC中，AB＝7，AD平分∠BAC，DE⊥AC于E，DE＝2，则△ABD的面积为（ ）
A．14B．12C．10D．7
【分析】过D点作DF⊥AB于F，如图，根据角平分线的性质得到DF＝DE＝2，然后利用三角形面积公式进行计算．
【解答】解：过D点作DF⊥AB于F，如图，
∵AD平分∠BAC，DE⊥AC，DF⊥AB，
∴DF＝DE＝2，
∴．
故选：D．
【点评】本题考查了角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解题的关键．
12．（3分）如图，把一张长方形纸片ABCD沿AF折叠，点F在边CD上，点D落在D′处，若∠ABD＝28°，AD′∥DB，则∠DAF的度数为（ ）
A．32°B．46°C．59°D．60°
【分析】由AD′∥DB，利用“两直线平行，内错角相等”，可得出∠D′AB的度数，再利用折叠的性质及∠DAF+∠D′AF＝∠DAB+∠F′AB，即可求出∠DAF的度数．
【解答】解：∵AD′∥DB，
∴∠D′AB＝∠ABD＝28°．
由折叠的性质，可得：∠DAF＝∠D′AF，
∵∠DAF+∠D′AF＝∠DAB+∠F′AB，
∴∠DAF＝（∠DAB+∠D′AB）＝×（90°+28°）＝59°．
故选：C．
【点评】本题考查了平行线的性质以及翻折变换（折叠问题），利用平行线的性质及折叠的性质，求出∠DAF的度数是解题的关键．
二、填空题：本大题共6小题，每小题3分，共18分．
13．（3分）如图，已知∠BOF＝120°，则∠A+∠B+∠C+∠D+∠E+∠F＝ 240° ．
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A+∠C，∠B+∠D，再根据邻补角求出∠EOF，然后求解即可．
【解答】解：如图，如图，根据三角形的外角性质，∠1＝∠A+∠C，∠2＝∠B+∠D，
∵∠BOF＝120°，
∴∠3＝180°﹣120°＝60°，
根据三角形内角和定理，∠E+∠1＝180°﹣60°＝120°，
∠F+∠2＝180°﹣60°＝120°，
所以，∠1+∠2+∠E+∠F＝120°+120°＝240°，
即∠A+∠B+∠C+∠D+∠E+∠F＝240°．
故答案为：240°．
【点评】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并把各角进行转化是解题的关键．
14．（3分）如图，在△ACD和△BDC中，∠A＝∠B＝90°，AD＝BC，∠ACD＝35°，则∠ACB＝ 20 °．
【分析】根据HL定理判定三角形全等，然后根据全等三角形的性质分析求解．
【解答】解：∵∠A＝∠B＝90°，
在Rt△ACD和Rt△BDC中，
，
∴Rt△ACD≌Rt△BDC（HL），
∴∠ACD＝∠BDC＝35°，
∴∠ACB＝180°﹣∠B﹣∠BDC﹣∠ACD＝20°，
故答案为：20．
【点评】本题考查全等三角形的判定和性质，理解用HL判断直角三角形全等的方法是解题关键．
15．（3分）三角形的三边长分别为5，1+2x，8，则x的取值范围是 1＜x＜6 ．
【分析】根据三角形的三边关系：任意两边之和大于第三边，任意两边之差小于第三边．
【解答】解：由题意，有8﹣5＜1+2x＜8+5，
解得：1＜x＜6．
【点评】考查了三角形的三边关系，还要熟练解不等式．
16．（3分）如图，在等边三角形ABC中，BC＝4，D是AB的中点，过点D作DF⊥AC于点F．过点F作FE⊥BC于点E，则EC的长为 ．
【分析】根据在直角三角形中，30°角所对的直角边等于斜边的一半，求得AF，CF，CE，再由等边三角形ABC的边长为4，得出EC的长．
【解答】解：∵△ABC为等边三角形，BC＝4，
∴∠A＝∠C＝60°，AB＝AC＝BC＝4，
∵DF⊥AC，FE⊥BC，
∴∠AFD＝∠CEF＝90°，
∴∠ADF＝∠CFE＝30°，
∴，
∵D是AB的中点，
∴AD＝2，
∴AF＝1，
∴CF＝3，
∴，
故答案为：．
【点评】本题考查等边三角形的性质及应用，熟练掌握等边三角形的性质和含30°角的直角三角形的性质是解题的关键．
17．（3分）如图，在△ABC中，AF平分∠BAC，AC的垂直平分线交BC于点E，∠B＝70°，∠FAE＝19°，则∠C＝ 24 度．
【分析】根据线段的垂直平分线的性质得到EA＝EC，得到∠EAC＝∠C，根据角平分线的定义、三角形内角和定理计算即可．
【解答】解：∵DE是AC的垂直平分线，
∴EA＝EC，
∴∠EAC＝∠C，
∴∠FAC＝∠EAC+19°，
∵AF平分∠BAC，
∴∠FAB＝∠EAC+19°，
∵∠B+∠BAC+∠C＝180°，
∴70°+2（∠C+19°）+∠C＝180°，
解得，∠C＝24°，
故答案为：24．
【点评】本题考查的是线段的垂直平分线的性质、三角形内角和定理，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
18．（3分）如图，AD为∠CAF的角平分线，BD＝CD，过D作DE⊥AC于E，DF⊥AB交BA的延长线于F，则下列结论：①△CDE≌△BDF；②CE＝AB+AE；③∠BDC＝∠BAC；④∠DAF＝∠CBD．其中正确结论的序号有 ①②③④ ．
【分析】根据角平分线上的点到角的两边距离相等可得DE＝DF，再利用“HL”证明Rt△CDE和Rt△BDF全等，根据全等三角形对应边相等可得CE＝AF，利用“HL”证明Rt△ADE和Rt△ADF全等，根据全等三角形对应边相等可得AE＝AF，然后求出CE＝AB+AE；根据全等三角形对应角相等可得∠DBF＝∠DCE，利用“8字型”证明∠BDC＝∠BAC；∠DAE＝∠CBD，再根据全等三角形对应角相等可得∠DAE＝∠DAF，然后求出∠DAF＝∠CBD．
【解答】解：∵AD平分∠CAF，DE⊥AC，DF⊥AB，
∴DE＝DF，
在Rt△CDE和Rt△BDF中，
，
∴Rt△CDE≌Rt△BDF（HL），故①正确；
∴CE＝AF，
在Rt△ADE和Rt△ADF中，
，
∴Rt△ADE≌Rt△ADF（HL），
∴AE＝AF，
∴CE＝AB+AF＝AB+AE，故②正确；
∵Rt△CDE≌Rt△BDF，
∴∠DBF＝∠DCE，
∵∠AOB＝∠COD，（设AC交BD于O），
∴∠BDC＝∠BAC，故③正确；
∴∠DAE＝∠DCB，
∵∠DBC＝∠DCB，
∴∠DAE＝∠DBC，
∵AD为∠CAF的角平分线，
∴∠DAE＝∠DAF，
∴∠DAF＝∠CBD，故④正确；
综上所述，正确的结论有①②③④共4个．
故答案为：①②③④
【点评】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记性质并准确识图判断出全等的三角形是解题的关键，难点在于需要二次证明三角形全等．
三、解答题：本大题共6小题，共46分，解答应写出文字说明，演算步骤或证明过程．
19．（6分）如图，在△ABC中，∠BAC＝56°，∠B＝43°，AD平分∠BAC，M是BC延长线上一点，过点M作MF⊥AD，垂足为H，MF分别与AB，AC交于点F，E．求∠M的度数．
【分析】由角平分线的定义得∠BAD＝28°，由外角性质可得∠ADM＝71°，然后根据三角形的内角和即可求解．
【解答】解：∵AD平分∠BAC，
∴，
∴∠ADM＝∠BAD+∠B＝28°+43°＝71°，
∵MH⊥AD，
∴∠MHD＝90°，
∴∠M＝180°﹣90°﹣71°＝19°．
【点评】本题考查了三角形的内角和定理，角平分线的定义，解题的关键是理解题意，灵活运用所学知识解决问题．
20．（6分）如图，△ABC顶点坐标分别为A（1，4），B（﹣2，1），C（3，2）．将△ABC关于x轴对称△A′B′C′．
（1）请你画出△A′B′C′，并写出点A′，B′，C′的坐标；
（2）连接B′C，C′C，求△CB′C′的面积．
【分析】（1）分别作出A，B，C关于x轴的对称点，再连成三角形，写出A'，B'，C'的坐标即可；
（2）结合图形，用三角形面积可得答案．
【解答】解：（1）如图：
△A′B′C′即为所求；
A'坐标为（1，﹣4）；B'的坐标为（﹣2，﹣1），C'的坐标为（3，﹣2）；
（2）∵×4×5＝10，
∴△CB′C′的面积是10．
【点评】本题考查作图﹣轴对称作图，解题的关键是掌握对称的性质．
21．（8分）如图，在△ABC中，AD平分∠BAC，过线段CD上一点E作EG∥AD，交AC于点F，交BA的延长线于点G．
（1）求证：△AFG是等腰三角形．
（2）若CE＝EF，∠BAC＝80°，求∠B的度数．
【分析】（1）结合角平分线的性质，根据平行线的性质得到∠BAD＝∠G，∠CAD＝∠AFG，然后等量代换可知∠G＝∠AFG，故△AFG是等腰三角形；
（2）根据等边对等角可得∠CFE＝∠C，结合（1）可得∠C＝∠CAD，再根据角平分线及三角形的内角和定理即可求解．
【解答】（1）证明：∵AD平分∠BAC，
∴∠BAD＝∠CAD．
∵EG∥AD，
∴∠BAD＝∠G，∠CAD＝∠AFG，
∴∠G＝∠AFG，
∴AF＝AG，
∴△AFG是等腰三角形．
（2）解：∵CE＝EF，
∴∠CFE＝∠C．
∵∠AFG＝∠CFE，∠AFG＝∠CAD，
∴∠C＝∠CAD．
∵∠BAC＝80°，AD平分∠BAC，
∴∠C＝∠CAD＝40°，
∴∠B＝180°﹣∠BAC﹣∠C＝60°．
【点评】本题考查了等腰三角形的判定及性质，平行线的性质，解决本题的关键是掌握等腰三角形的判定定理．
22．（8分）如图，BE＝CF，DE⊥AB的延长线于点E，DF⊥AC于点F，且DB＝DC，
求证：AD是∠BAC的平分线．
【分析】先根据全等三角形的判定定理得出Rt△BDE≌Rt△CDF，进而得出DE＝DF，由角平分线的判定可知AD是∠BAC的平分线．
【解答】证明：∵DE⊥AB的延长线于点E，DF⊥AC于点F，
∴∠BED＝∠CFD＝90°，
∴△BDE与△CDF是直角三角形，
，
∴Rt△BDE≌Rt△CDF（HL），
∴DE＝DF，
∴AD是∠BAC的平分线．
【点评】本题考查的是角平分线的判定及全等三角形的判定与性质，熟知到角的两边的距离相等的点在角的平分线上是解答此题的关键．
23．（8分）如图，在△ABC中，∠A＝50°，DE垂直平分BC，∠ABC的角平分线BF交DE于△ABC内一点P，连接PC．若∠ACP＝28°，求∠ABP的度数．
【分析】根据线段垂直平分线的性质，可得∠PBC＝∠PCB，根据角平分线的定义，可得∠PBC＝∠PCB＝∠ABP，最后根据三角形内角和定理，即可得到∠ABP的度数．
【解答】解：∵DE垂直平分BC，
∴PB＝PC，
∴∠PBC＝∠PCB，
∵BP平分∠ABC，
∴∠PBC＝∠ABP，
∴∠PBC＝∠PCB＝∠ABP，
∵∠A＝50°，∠ACP＝28°，
∴∠PBC+∠PCB+∠ABP＝180°﹣50°﹣28°＝102°，
∴3∠ABP＝102°，
∴∠ABP＝34°．
【点评】本题主要考查了线段垂直平分线的性质的运用，解题时注意：线段垂直平分线上任意一点，到线段两端点的距离相等．
24．（10分）如图所示，直线AB交x轴于点A（4，0），交y轴于点B（0，﹣4）．
（1）如图1，若点C的坐标为（﹣1，0），且AH⊥BC于点H，AH交OB于点P．求证：△OAP≌△OBC．
（2）如图2，若点D为AB的中点，点M为y轴正半轴上一动点，连接MD，过D作DN⊥DM交x轴于N点，当M点在y轴正半轴上运动的过程中，
①线段OM与AN有什么数量关系？
②若S表示三角形的面积，式子S△BDM﹣S△ADN的值是否发生改变？如发生改变，求出该式子的值的变化范围；若不改变，写出该式子的值．
【分析】（1）用ASA证明△OAP≌△OBC（ASA），即可求解；
（2）①证明△MOD≌△NAD（ASA），即可求解；
（2）点D为AB的中点，则S△DOB＝×S△AOB＝×8＝4，而△MOD≌△NAD，则S△BDM﹣S△ADN＝S△BDM﹣S△MOD＝S△DOB＝4，即可求解．
【解答】（1）证明：∵点A的坐标为（4，0），点B的坐标为（0，﹣4），
∴OA＝OB，
∵∠AOP＝90°，∠BHP＝90°，
∴∠AOP＝∠BHP，
∵∠APO＝∠BPH，
∴∠OAP＝∠OBC，
在△OAP和△OBC中，∠OAP＝∠OBC，OA＝OB，∠AOP＝∠BOC，
∴△OAP≌△OBC（ASA）；
（2）解：①线段OM＝AN，
理由如下：如图2，连接OD，
∵∠AOB＝90°，OA＝OB，点D为AB的中点，
∴OD⊥AB，OD＝OA＝OB，∠BOD＝∠AOD＝∠OAD＝45°，
∴∠MOD＝135°，∠NAD＝135°，
∴∠MOD＝∠NAD，
∵∠ODA＝∠MDN＝90°，
∴∠MDO＝∠NDA，
在△MOD和△NAD中，∠MOD＝∠NAD，OD＝AD，∠MDO＝∠NDA，
∴△MOD≌△NAD（ASA），
∴OM＝AN；
（2）式子S△BDM﹣S△ADN的值不发生改变，
理由如下：S△AOB＝×4×4＝8，
∵点D为AB的中点，
∴S△DOB＝×S△AOB＝×8＝4，
∵△MOD≌△NAD，
∴S△BDM﹣S△ADN＝S△BDM﹣S△MOD＝S△DOB＝4．
【点评】本题考查的是一次函数综合运用，涉及到三角形全等、面积的计算等，证明三角形全等是解题的关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/11/25 14:09:58；用户：18328501451；邮箱：18328501451；学号：43314264