第26讲 动量守恒定律及其应用（讲义）（解析版）-2025年高考物理一轮复习讲练测（新教材新高考）

这是一份第26讲 动量守恒定律及其应用（讲义）（解析版）-2025年高考物理一轮复习讲练测（新教材新高考），共28页。
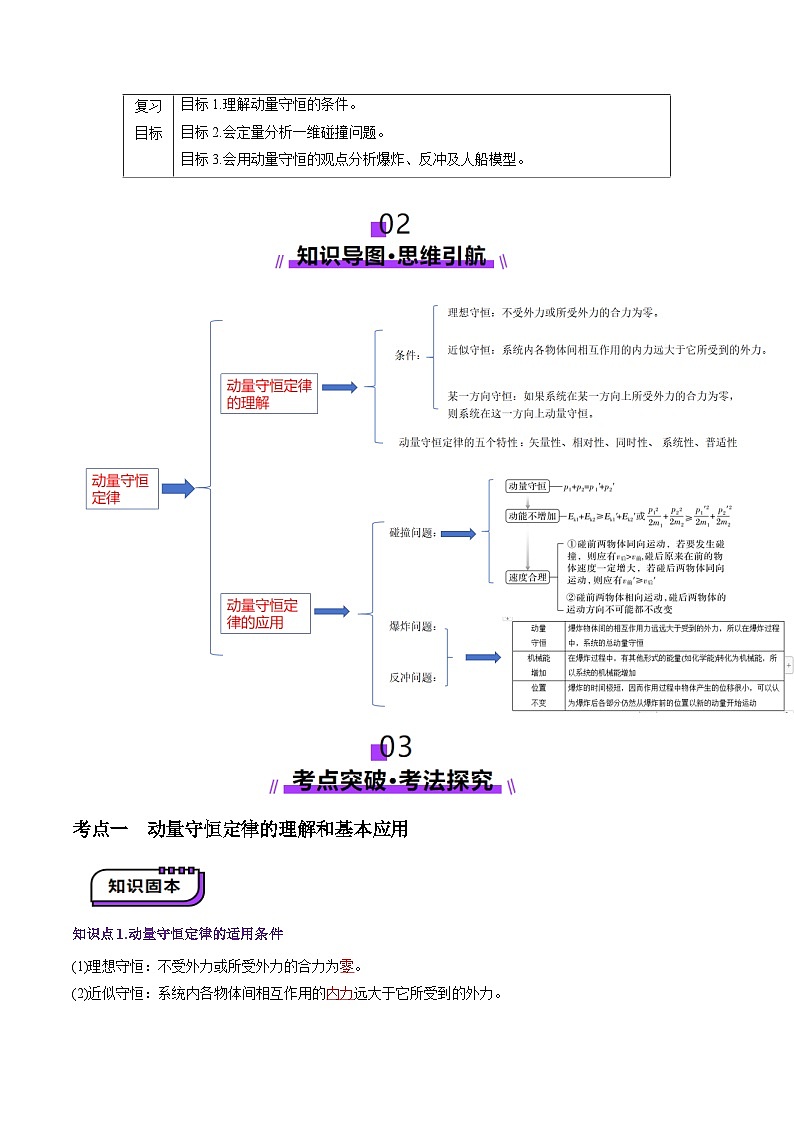
\l "_Tc16510" 02、知识导图，思维引航 PAGEREF _Tc16510 \h 2
\l "_Tc13809" 03、考点突破，考法探究 PAGEREF _Tc13809 \h 3
\l "_Tc18222" 考点一 动量守恒定律的理解和基本应用 PAGEREF _Tc18222 \h 3
\l "_Tc2285" 知识点1.动量守恒定律的适用条件 PAGEREF _Tc2285 \h 3
\l "_Tc9152" 知识点2.动量守恒定律的五个特性 PAGEREF _Tc9152 \h 3
考向洞察
\l "_Tc12743" 考向1.动量守恒定律的理解 PAGEREF _Tc12743 \h 3
\l "_Tc12319" 考向2.动量守恒定律的基本应用 PAGEREF _Tc12319 \h 4
\l "_Tc12282" 考点二 碰撞问题 PAGEREF _Tc12282 \h 6
\l "_Tc9011" 知识点1．碰撞类问题遵循的三条原则 PAGEREF _Tc9011 \h 6
\l "_Tc1755" 知识点2．弹性碰撞讨论 PAGEREF _Tc1755 \h 6
\l "_Tc8921" 知识点3.非弹性碰撞 PAGEREF _Tc8921 \h 7
\l "_Tc15658" 考向洞察 PAGEREF _Tc15658 \h 7
\l "_Tc6599" 考向1.碰撞的可能性分析 PAGEREF _Tc6599 \h 7
\l "_Tc24050" 考向2.弹性碰撞的应用 PAGEREF _Tc24050 \h 8
\l "_Tc11611" 考向3.非弹性碰撞 PAGEREF _Tc11611 \h 9
\l "_Tc11666" 考点三 爆炸、反冲和“人船”模型 PAGEREF _Tc11666 \h 10
\l "_Tc23310" 知识点1.爆炸现象的三个规律 PAGEREF _Tc23310 \h 10
\l "_Tc7141" 知识点2.反冲运动的三点说明 PAGEREF _Tc7141 \h 10
\l "_Tc17003" 知识点3.人船模型及其拓展 PAGEREF _Tc17003 \h 10
\l "_Tc1257" 考向洞察 PAGEREF _Tc1257 \h 11
\l "_Tc1966" 考向1.两体爆炸模型 PAGEREF _Tc1966 \h 11
\l "_Tc6993" 考向2.反冲运动 PAGEREF _Tc6993 \h 12
\l "_Tc23680" 考向3.人船模型及其拓展模型 PAGEREF _Tc23680 \h 13
04、真题练习，命题洞见 \l "_Tc29921" PAGEREF _Tc29921 \h 15
考点一 动量守恒定律的理解和基本应用
知识点1.动量守恒定律的适用条件
(1)理想守恒：不受外力或所受外力的合力为零。
(2)近似守恒：系统内各物体间相互作用的内力远大于它所受到的外力。
(3)某一方向守恒：如果系统在某一方向上所受外力的合力为零，则系统在这一方向上动量守恒。
知识点2.动量守恒定律的五个特性
考向1.动量守恒定律的理解
1.如图，光滑水平地面上有一小车，一轻弹簧的一端与车厢的挡板相连，另一端与滑块相连，滑块与车厢的水平底板间有摩擦。用力向右推动车厢使弹簧压缩，撤去推力时滑块在车厢底板上有相对滑动。在地面参考系(可视为惯性系)中，从撤去推力开始，小车、弹簧和滑块组成的系统( )
A.动量守恒，机械能守恒
B.动量守恒，机械能不守恒
C.动量不守恒，机械能守恒
D.动量不守恒，机械能不守恒
【答案】 B
【解析】 撤去推力，系统所受合外力为0，动量守恒，滑块和小车之间有滑动摩擦力，由于摩擦生热，系统机械能减少，故B正确。
2.如图所示，A、B两木块紧靠在一起且静止于光滑水平面上，木块C以一定的初速度v0从A的左端开始向右滑行，最后停在B木块的右端，对此过程，下列叙述不正确的是( )
A.当C在A上滑行时，A、C组成的系统动量守恒
B.当C在B上滑行时，B、C组成的系统动量守恒
C.无论C是在A上滑行还是在B上滑行，A、B、C三木块组成的系统动量都守恒
D.当C在B上滑行时，A、B、C组成的系统动量守恒
【答案】A
【解析】 当C在A上滑行时，对A、C组成的系统受力分析，B对A的作用力为外力，合外力不等于0，故系统动量不守恒，A错误；当C在B上滑行时，A、B已分离，对B、C组成的系统，沿水平方向不受外力作用，故系统动量守恒，B正确；对A、B、C三木块组成的系统，无论C是在A上滑行还是在B上滑行，系统的水平方向上都无外力作用，系统动量守恒，C、D正确。
3．如图所示，将一光滑的半圆槽置于光滑水平面上，槽的左侧紧靠在墙壁上。现让一小球自左侧槽口A的正上方从静止开始落下，自A点与圆弧槽相切进入槽内，则下列结论中正确的是( )
A．小球在半圆槽内运动的全过程中，只有重力对它做功
B．小球在半圆槽内运动的全过程中，小球与半圆槽在水平方向动量守恒
C．小球自半圆槽B点向C点运动的过程中，小球与半圆槽在水平方向动量守恒
D．小球离开C点以后，将做竖直上抛运动
【答案】C
【解析】： 小球下滑到半圆槽的最低点B之后，半圆槽离开墙壁，除了重力外，槽对小球的弹力也对小球做功，选项A错误；小球下滑到半圆槽的最低点B之前，小球与半圆槽组成的系统水平方向上受到墙壁的弹力作用，系统所受的外力不为零，系统水平方向上动量不守恒，半圆槽离开墙壁后，小球与半圆槽在水平方向动量守恒，选项B错误，C正确；半圆槽离开墙壁后小球对槽的压力对槽做功，小球与半圆槽具有向右的水平速度，所以小球离开右侧槽口以后，将做斜上抛运动，选项D错误。
考向2.动量守恒定律的基本应用
4．随着机动车数量的增加，交通安全问题日益凸显，分析交通违法事例，将警示我们遵守交通法规，珍惜生命。已知某限速60 km/h的平直公路上，一辆质量为m1＝800 kg的汽车A以速度v1＝15 m/s 沿平直公路行驶时，驾驶员发现前方不远处有一质量m2＝1 200 kg的汽车B以速度v2迎面驶来，两车立即同时急刹车，使车做匀减速运动，但两车仍在开始刹车t＝1 s后猛烈地相撞，相撞后结合在一起再沿B车原行驶方向滑行6 m后停下，设两车与路面间动摩擦因数μ＝0.3, g取10 m/s2，忽略碰撞过程中路面摩擦力的冲量，求：
(1)两车碰撞后刚结合在一起时的速度大小；
(2)求B车刹车前的速度，并判断B车是否超速。
【答案】：(1)6 m/s (2)21 m/s，超速
【解析】：(1)对于碰撞后共同滑行过程有a＝eq \f(μmg,m)＝μg
x＝eq \f(v共2,2a)，可得v共＝6 m/s。
(2)对A车有：vA＝v1－at
对B车有：vB＝v2－at
以碰撞前A车运动的方向为正方向，对碰撞过程由动量守恒定律得：
m1vA－m2vB＝－(m1＋m2)v共
可得v2＝21 m/s>60 km/h
故B车超速。
5. (多选)足够大的光滑水平面上，一根不可伸长的细绳一端连接着质量为m1＝1.0 kg的物块A，另一端连接质量为m2＝1.0 kg的长木板B，绳子开始是松弛的。质量为m3＝1.0 kg的物块C放在长木板B的右端，C与长木板B间的滑动摩擦力的大小等于最大静摩擦力大小。现在给物块C水平向左的瞬时初速度v0＝2.0 m/s，物块C立即在长木板B上运动。已知绳子绷紧前，B、C已经达到共同速度；绳子绷紧后，A、B总是具有相同的速度；物块C始终未从长木板B上滑落。下列说法正确的是( )
A.绳子绷紧前，B、C达到的共同速度大小为1.0 m/s
B.绳子刚绷紧后的瞬间，A、B的速度大小均为1.0 m/s
C.绳子刚绷紧后的瞬间，A、B的速度大小均为0.5 m/s
D.最终A、B、C三者将以大小为eq \f(2,3) m/s的共同速度一直运动下去
【答案】 ACD
【解析】 绳子绷紧前，B、C已经达到共同速度，设B、C达到的共同速度大小为v1，根据动量守恒定律可得m3v0＝(m2＋m3)v1，解得v1＝1.0 m/s，A正确；绳子刚绷紧后的瞬间，设A、B具有相同的速度v2，A、B组成的系统满足动量守恒，则有m2v1＝(m1＋m2)v2，解得v2＝0.5 m/s，B错误，C正确；A、B、C三者最终有共同的速度，设为v3，A、B、C组成的系统满足动量守恒，则有m3v0＝(m1＋m2＋m3)v3，解得v3＝eq \f(2,3) m/s，D正确。
考点二 碰撞问题
知识点1．碰撞类问题遵循的三条原则
知识点2．弹性碰撞讨论
(1)碰后速度的求解：
根据动量守恒定律和机械能守恒定律
eq \b\lc\{\rc\ (\a\vs4\al\c1(m1v1＋m2v2＝m1v1′＋m2v2′ ①,\f(1,2)m1v12＋\f(1,2)m2v22＝\f(1,2)m1v1′2＋\f(1,2)m2v2′2 ②))
解得v1′＝eq \f(m1－m2v1＋2m2v2,m1＋m2)，
v2′＝eq \f(m2－m1v2＋2m1v1,m1＋m2)。
(2)分析讨论：
当碰前物体2的速度不为零时，若m1＝m2，则：
v1′＝v2，v2′＝v1，即两物体交换速度。
当碰前物体2的速度为零时，v2＝0，则：
v1′＝eq \f(m1－m2v1,m1＋m2)，v2′＝eq \f(2m1v1,m1＋m2)。
①m1＝m2时，v1′＝0，v2′＝v1，碰撞后两物体交换速度。
②m1＞m2时，v1′＞0，v2′＞0，碰撞后两物体沿相同方向运动。
③m1＜m2时，v1′＜0，v2′＞0，碰撞后质量小的物体被反弹回来。
知识点3.非弹性碰撞
1.非弹性碰撞
碰撞结束后，动能有部分损失。
m1v1＋m2v2＝m1v1′＋m2v2′
eq \f(1,2)m1veq \\al(2,1)＋eq \f(1,2)m2veq \\al(2,2)＝eq \f(1,2)m1v1′2＋eq \f(1,2)m2v2′2＋ΔEk损
2.完全非弹性碰撞
碰撞结束后，两物体合二为一，以同一速度运动，动能损失最大。
m1v1＋m2v2＝(m1＋m2)v
eq \f(1,2)m1veq \\al(2,1)＋eq \f(1,2)m2veq \\al(2,2)＝eq \f(1,2)(m1＋m2)v2＋ΔEk损max
结果：v＝eq \f(m1v1＋m2v2,m1＋m2)
ΔEk损max＝eq \f(m1m2,2（m1＋m2）)(v1－v2)2
3.静止物体被撞后的速度范围
物体A与静止的物体B发生碰撞，当发生完全非弹性碰撞时损失的机械能最多，物体B的速度最小，vB＝eq \f(mA,mA＋mB)v0，当发生弹性碰撞时，物体B速度最大，vB＝eq \f(2mA,mA＋mB)v0。则碰后物体B的速度范围为eq \f(mA,mA＋mB)v0≤vB≤eq \f(2mA,mA＋mB)v0。
考向1.碰撞的可能性分析
1.如图为某运动员正在准备击球，设在某一杆击球过程中，白色球(主球)和花色球碰撞前后都在同一直线上运动，碰前白色球A的动量pA＝5 kg· m/s，花色球B静止，碰后花色球B的动量变为pB′＝4 kg· m/s，则两球质量mA与mB间的关系可能是( )
A.mB＝eq \f(1,6)mA B.mB＝eq \f(1,4)mA
C.mB＝2mA D.mB＝5mA
【答案】 C
【解析】 碰撞过程系统动量守恒，以白色球的初速度方向为正方向，由动量守恒定律得pA＋pB＝pA′＋pB′，解得pA′＝1 kg· m/s，根据碰撞过程总动能不增加，则有eq \f(peq \\al(2,A),2mA)＋eq \f(peq \\al(2,B),2mB)≥eq \f(pA′2,2mA)＋eq \f(pB′2,2mB)，解得mB≥eq \f(2,3)mA，碰后，两球同向运动，A的速度不大于B的速度，则eq \f(pA′,mA)≤eq \f(pB′,mB)，解得mB≤4mA，综上可知eq \f(2,3)mA≤mB≤4mA，故C正确。
考向2.弹性碰撞的应用
2.如图所示，五个等大的小球B、C、D、E、F，沿一条直线静放在光滑水平面上，另一等大小球A沿该直线以速度v向 B球运动，小球间发生碰撞均为弹性碰撞。若B、C、D、E四个球质量相等，且比A、F两球质量均要大些，则所有碰撞结束后，还在运动的小球个数为( )
A．1个 B．2个
C．3个 D．4个
【答案】C
【解析】 球A、B发生弹性碰撞过程mv＝mv1＋Mv2，eq \f(1,2)mv2＝eq \f(1,2)mv12＋eq \f(1,2)Mv22，可得v1＝eq \f(m－M,m＋M)v，v2＝eq \f(2m,m＋M)v，即A球反弹，B球前进，然后B与C发生弹性碰撞，速度互换，B球停止，C球前进，以此类推，最后B、C、D停止，E与F发生弹性碰撞，可推得E、F都向右运动，速度不同，因此最后运动的是A、E、F球，故选C。
3.如图所示，两小球P、Q竖直叠放在一起，小球间留有较小空隙，从距水平地面高度为h处同时由静止释放。已知小球Q的质量是P的2倍。设所有碰撞均为弹性碰撞。忽略空气阻力及碰撞时间，则两球第一次碰撞后小球P上升的高度为( )
A.eq \f(5,3)h B.eq \f(25,9)h C.eq \f(7,3)h D.eq \f(49,9)h
【答案】 B
【解析】 设小球P、Q的质量分别为m、2m，落地前的瞬间二者速度均为v，由动能定理可得3mgh＝eq \f(1,2)×3mv2，解得v＝eq \r(2gh)，Q与地面碰撞后速度等大反向，然后与P碰撞，P、Q碰撞过程满足动量守恒、机械能守恒，规定向上为正方向，则有2mv－mv＝mvP＋2mvQ，eq \f(1,2)×3mv2＝eq \f(1,2)mvP2＋eq \f(1,2)×2mvQ2，解得vP＝eq \f(5,3)eq \r(2gh)，碰后小球P机械能守恒，则有mgh′＝eq \f(1,2)mvP2，解得h′＝eq \f(25,9)h，故选B。
考向3.非弹性碰撞
4.如图所示，光滑水平面上依次有滑块C质量mC＝2 kg，滑块A质量mA＝3 kg，滑块B质量mB＝3 kg。开始时A、B静止，C以初速度v0＝10 m/s的速度冲向A，与A发生弹性碰撞，碰撞后A继续向右运动，与B发生碰撞并粘在一起。求：
(1)C与A碰撞后A的速度大小为多少；
(2)A与B碰撞过程中损失的机械能。
【答案】 (1)8 m/s (2)48 J
【解析】 (1)取向右为正方向，以C、A为系统研究，根据动量守恒定律有
mCv0＝mCvC＋mAvA
根据机械能守恒定律有
eq \f(1,2)mCveq \\al(2,0)＝eq \f(1,2)mCveq \\al(2,C)＋eq \f(1,2)mAveq \\al(2,A)
解得vC＝－2 m/s，vA＝8 m/s
即C与A碰撞后A的速度大小为8 m/s。
(2)仍取向右为正方向，以A、B为系统研究，根据动量守恒定律有
mAvA＝eq \b\lc\(\rc\)(\a\vs4\al\c1(mA＋mB))v
根据能量守恒定律有
E损＝eq \f(1,2)mAveq \\al(2,A)－eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(mA＋mB))v2
解得E损＝48 J。
5.如图所示，超市为节省收纳空间，常常将手推购物车相互嵌套进行收纳。质量均为m＝16 kg的两辆购物车相距L1＝1 m静止在水平面上。第一辆车在工作人员猛推一下后，沿直线运动与第二辆车嵌套在一起，继续运动了L2＝1.25 m后停了下来。人推车时间、两车相碰时间极短，可忽略，车运动时受到的阻力恒为车重的0.25倍，重力加速度取g＝10 m/s2，求：
(1)两辆车从嵌套后运动到停下来所用时间；
(2)两辆车在嵌套过程中损失的机械能；
(3)工作人员对第一辆车所做的功。
【答案】 (1)1 s (2)100 J (3)240 J
【解析】 (1)对整体，由牛顿第二定律有
k×2mg＝2ma
解得a＝2.5 m/s2
逆向过程有L2＝eq \f(1,2)at2，解得t＝1 s。
(2)嵌套后，对整体有0＝v2－at，v2＝2.5 m/s
嵌套过程中有mv1＝2mv2，
解得v1＝5 m/s
在嵌套过程中损失的机械能
ΔE＝eq \f(1,2)mveq \\al(2,1)－eq \f(1,2)×2mveq \\al(2,2)
解得ΔE＝100 J。
(3)对第一辆小车，由动能定理得
W－kmgL1＝eq \f(1,2)mveq \\al(2,1)－0
解得W＝240 J。
考点三 爆炸、反冲和“人船”模型
知识点1.爆炸现象的三个规律
知识点2.反冲运动的三点说明
知识点3.人船模型及其拓展
1.模型图示
2.模型特点
(1)两物体满足动量守恒定律：mv人－Mv船＝0。
(2)两物体的位移大小满足：meq \f(x人,t)－Meq \f(x船,t)＝0，x人＋x船＝L得x人＝eq \f(M,M＋m)L，x船＝eq \f(m,M＋m)L。
3.运动特点
(1)人动则船动，人静则船静，人快船快，人慢船慢，人左船右。
(2)人船位移比等于它们质量的反比；人船平均速度(瞬时速度)比等于它们质量的反比，即eq \f(x人,x船)＝eq \f(v人,v船)＝eq \f(M,m)。
4.“人船模型”的拓展(某一方向动量守恒)
考向1.两体爆炸模型
1.双响爆竹是民间庆典使用较多的一种烟花爆竹，其结构简图如图所示，纸筒内分上、下两层安放火药。使用时首先引燃下层火药，使爆竹获得竖直向上的初速度，升空后上层火药被引燃，爆竹凌空爆响。一人某次在水平地面上燃放双响爆竹，爆竹上升至最高点时恰好引燃上层火药，立即爆炸成两部分，两部分的质量之比为1∶2，获得的速度均沿水平方向。已知这次燃放爆竹上升的最大高度为h，两部分落地点之间的距离为L，重力加速度为g，不计空气阻力，不计火药爆炸对爆竹总质量的影响。
(1)求引燃上层火药后两部分各自获得的速度大小。
(2)已知火药燃爆时爆竹增加的机械能与火药的质量成正比，求上、下两层火药的质量比。
【答案】 (1)eq \f(L,3) eq \r(\f(2g,h)) eq \f(L,3) eq \r(\f(g,2h)) (2)eq \f(L2,18h2)
【解析】(1)引燃上层火药后两部分向相反的方向做平抛运动，竖直方向h＝eq \f(1,2)gt2
水平方向L＝v1t＋v2t
上层火药燃爆时，水平方向动量守恒，设爆竹总质量为m，则有0＝eq \f(1,3)mv1－eq \f(2,3)mv2
解得两部分各自获得的速度大小v1＝eq \f(L,3) eq \r(\f(2g,h))，v2＝eq \f(L,3) eq \r(\f(g,2h))。
(2)上层火药燃爆后爆竹获得的机械能E上＝eq \f(1,2)×eq \f(1,3)mv12＋eq \f(1,2)×eq \f(2,3)mv22
下层火药燃爆后爆竹获得的机械能E下＝mgh
上、下两层火药的质量比eq \f(m上,m下)＝eq \f(E上,E下)＝eq \f(L2,18h2)。
2．(多选)一个质量为m的小型炸弹自水平地面朝右上方射出，在最高点以水平向右的速度v飞行时，突然爆炸为质量相等的甲、乙、丙三块弹片，如图所示。爆炸之后乙自静止自由下落，丙沿原路径回到原射出点。若忽略空气阻力，释放的化学能全部转化为动能，则下列说法正确的是( )
A．爆炸后乙落地的时间最长
B．爆炸后甲落地的时间最长
C．甲、丙落地点到乙落地点O的距离比为4∶1
D．爆炸过程释放的化学能为eq \f(7mv2,3)
【答案】CD
【解析】： 爆炸后甲、丙从同一高度平抛，乙从同一高度自由下落，则落地时间t＝eq \r(\f(2H,g))相等，选项A、B错误；爆炸过程动量守恒，有mv＝－eq \f(1,3)mv丙＋eq \f(1,3)mv甲，由题意知v丙＝v，得v甲＝4v，爆炸后甲、丙从同一高度平抛，落地点到乙落地点O的距离x＝vt，t相同，则x∝v，甲、丙落地点到乙落地点O的距离比为x甲∶x丙＝v甲∶v丙＝4∶1，选项C正确；根据能量守恒定律可得爆炸过程释放的化学能ΔE＝eq \f(1,2)×eq \f(m,3)v甲2＋eq \f(1,2)×eq \f(m,3)v丙2－eq \f(1,2)mv2＝eq \f(7,3)mv2，选项D正确。
考向2.反冲运动
3.一火箭喷气发动机每次喷出质量m＝200 g的气体，气体离开发动机喷出时的速度v＝1 000 m/s。设火箭(包括燃料)质量M＝300 kg，发动机每秒喷气20次，火箭初始时静止(结果保留1位小数)。
(1)当发动机第三次喷出气体后，火箭的速度为多大？
(2)运动第1 s末，火箭的速度为多大？
【答案】 (1)2.0 m/s (2)13.5 m/s
【解析】 (1)设喷出三次气体后火箭的速度为v3，以火箭和喷出的三次气体为研究对象，由动量守恒定律得(M－3m)v3－3mv＝0，解得v3≈2.0 m/s。
(2)发动机每秒喷气20次，设运动第1 s末，火箭的速度为v20，以火箭和喷出的20次气体为研究对象，根据动量守恒定律得(M－20m)v20－20mv＝0，解得v20≈13.5 m/s。
4.如图所示，某中学航天兴趣小组的同学将静置在地面上的质量为M(含水)的自制“水火箭”释放升空，在极短的时间内，质量为m的水以相对地面为v0的速度竖直向下喷出。已知重力加速度为g，空气阻力不计，下列说法正确的是( )
A．火箭的推力来源于火箭外的空气对它的反作用力
B．水喷出的过程中，火箭和水机械能守恒
C．火箭获得的最大速度为eq \f(M,M－m)v0
D．火箭上升的最大高度为eq \f(m2v02,2gM－m2)
【答案】D
【解析】： 火箭的推力来源于火箭里喷出的水对它的反作用力，故A错误；水喷出的过程中，瓶内气体做功，火箭和水机械能不守恒，故B错误；由动量守恒定理可得(M－m)v＝mv0，解得v＝eq \f(mv0,M－m)，故C错误；水喷出后，火箭做竖直上抛运动，由题意有v2＝2gh，h＝eq \f(\b\lc\(\rc\)(\a\vs4\al\c1(\f(mv0,M－m)))2,2g)＝eq \f(m2v02,2gM－m2)，故D正确。
考向3.人船模型及其拓展模型
5.如图所示，质量为M＝4 kg的小车静止在光滑水平面上，小车AB段是半径为R＝1 m 的四分之一光滑圆弧轨道，BC段是长为L的粗糙水平轨道，两段轨道相切于B点。一质量为m＝1 kg 的可视为质点的滑块从小车上的A点由静止开始沿AB轨道下滑，然后滑入BC轨道，最后恰好停在C点，滑块与BC轨道间的动摩擦因数为0.5，重力加速度为g＝10 m/s2，则( )
A．整个过程中滑块和小车组成的系统动量守恒
B．滑块由A滑到B过程中，滑块的机械能守恒
C．BC段长L＝1 m
D．全过程小车相对地面的位移大小为0.6 m
【答案】 D
【解析】 滑块在圆弧轨道上运动时有竖直方向的加速度，所以对系统而言竖直方向外力矢量和不为零，不满足动量守恒的条件，故A错误；滑块由A滑到B过程中，小车对滑块的弹力做负功，滑块的机械能不守恒，故B错误；滑块恰好停在C点时，二者均静止，根据能量守恒定律有mgR＝μmgL，解得L＝2 m，故C错误；根据系统水平方向动量守恒有Mv1＝mv2，通过相同的时间有Mx1＝mx2，且有x1＋x2＝R＋L，解得x1＝0.6 m，故D正确。
6.质量为m的人在质量为M的小车上从左端走到右端，如图所示，当车与地面摩擦不计时，那么( )
A．人在车上行走，若人相对车突然停止，则车由于惯性过一会才停止
B．人在车上行走的平均速度越大，则车在地面上移动的距离也越大
C．人在车上行走的平均速度越小，则车在地面上移动的距离就越大
D．不管人以什么样的平均速度行走，车在地面上移动的距离相同
【答案】D
【解析】： 由人与车组成的系统动量守恒，初态系统总动量为零，则有mv人＝Mv车，若人相对车突然停止，则车也突然停止，故A错误；设车长为L，由m(L－x车)＝Mx车，解得x车＝eq \f(m,M＋m)L，车在地面上移动的位移大小与人的平均速度大小无关，故D正确，B、C错误。
7.一个质量为M、底面边长为b的斜面体静止于光滑的水平桌面上，如图所示，有一质量为m的物块由斜面顶部无初速度滑到底部时，斜面体移动的距离为s。下列说法中正确的是( )
A．若斜面粗糙，则s＝eq \f(mb,M＋m)
B．只有斜面光滑，才有s＝eq \f(mb,M＋m)
C．若斜面光滑，则下滑过程中系统动量守恒，机械能守恒
D．若斜面粗糙，则下滑过程中系统动量守恒，机械能不守恒
【答案】A
【解析】： 不论斜面是否光滑，斜面体和物块组成的系统在水平方向上都动量守恒，以向左为正方向，斜面体的位移大小为s，则物块的位移大小为b－s，物块和斜面体的平均速率分别为v1＝eq \f(b－s,t)，v2＝eq \f(s,t)，由动量守恒定律得mv1－Mv2＝0，解得s＝eq \f(mb,M＋m)，A正确，B错误；不论斜面是否光滑，物块下滑过程中系统在竖直方向上所受合力都不为零，系统所受的合力不为零，所以系统动量不守恒，若斜面光滑，则系统机械能守恒，若斜面不光滑，则系统机械能不守恒，C、D错误。
1．（2024·安徽·高考真题）在某装置中的光滑绝缘水平面上，三个完全相同的带电小球，通过不可伸长的绝缘轻质细线，连接成边长为d的正三角形，如图甲所示。小球质量为m，带电量为，可视为点电荷。初始时，小球均静止，细线拉直。现将球1和球2间的细线剪断，当三个小球运动到同一条直线上时，速度大小分别为、、，如图乙所示。该过程中三个小球组成的系统电势能减少了，k为静电力常量，不计空气阻力。则（ ）
A．该过程中小球3受到的合力大小始终不变B．该过程中系统能量守恒，动量不守恒
C．在图乙位置，，D．在图乙位置，
【答案】D
【详解】AB．该过程中系统动能和电势能相互转化，能量守恒，对整个系统分析可知系统受到的合外力为0，故动量守恒；当三个小球运动到同一条直线上时，根据对称性可知细线中的拉力相等，此时球3受到1和2的电场力大小相等，方向相反，故可知此时球3受到的合力为0，球3从静止状态开始运动，瞬间受到的合力不为0，故该过程中小球3受到的合力在改变，故AB错误；
CD．对系统根据动量守恒
根据球1和2运动的对称性可知，解得
根据能量守恒
解得
故C错误，D正确。
故选D。
2．（2024·江苏·高考真题）在水平面上有一个U形滑板A，A的上表面有一个静止的物体B，左侧用轻弹簧连接在物体B的左侧，右侧用一根细绳连接在物体B的右侧，开始时弹簧处于拉伸状态，各表面均光滑，剪断细绳后，则（ ）
A．弹簧原长时B动量最大
B．压缩最短时A动能最大
C．系统动量变大
D．系统机械能变大
【答案】A
【详解】对整个系统分析可知合外力为0，A和B组成的系统动量守恒，得
设弹簧的初始弹性势能为，整个系统只有弹簧弹力做功，机械能守恒，当弹簧原长时得
联立得
故可知弹簧原长时物体速度最大，此时动量最大，动能最大。对于系统来说动量一直为零，系统机械能不变。
故选A。
3．（2024·广东·高考真题）如图所示，光滑斜坡上，可视为质点的甲、乙两个相同滑块，分别从、高度同时由静止开始下滑。斜坡与水平面在O处平滑相接，滑块与水平面间的动摩擦因数为，乙在水平面上追上甲时发生弹性碰撞。忽略空气阻力。下列说法正确的有（ ）
A．甲在斜坡上运动时与乙相对静止
B．碰撞后瞬间甲的速度等于碰撞前瞬间乙的速度
C．乙的运动时间与无关
D．甲最终停止位置与O处相距
【答案】ABD
【详解】A．两滑块在光滑斜坡上加速度相同，同时由静止开始下滑，则相对速度为0，故A正确；
B．两滑块滑到水平面后均做匀减速运动，由于两滑块质量相同，且发生弹性碰撞，可知碰后两滑块交换速度，即碰撞后瞬间甲的速度等于碰撞前瞬间乙的速度，故B正确；
C．设斜面倾角为θ，乙下滑过程有
在水平面运动一段时间t2后与甲相碰，碰后以甲碰前速度做匀减速运动t3，乙运动的时间为
由于t1与有关，则总时间与有关，故C错误；
D．乙下滑过程有
由于甲和乙发生弹性碰撞，交换速度，则可知甲最终停止位置与不发生碰撞时乙最终停止的位置相同；则如果不发生碰撞，乙在水平面运动到停止有
联立可得
即发生碰撞后甲最终停止位置与O处相距。故D正确。
故选ABD。
4．（2024·广西·高考真题）如图，在光滑平台上有两个相同的弹性小球M和N。M水平向右运动，速度大小为v。M与静置于平台边缘的N发生正碰，碰撞过程中总机械能守恒。若不计空气阻力，则碰撞后，N在（ ）
A．竖直墙面上的垂直投影的运动是匀速运动
B．竖直增面上的垂直投影的运动是匀加速运动
C．水平地面上的垂直投影的运动速度大小等于v
D．水平地面上的垂直投影的运动速度大小大于v
【答案】BC
【详解】由于两小球碰撞过程中机械能守恒，可知两小球碰撞过程是弹性碰撞，由于两小球质量相等，故碰撞后两小球交换速度，即
，
碰后小球N做平抛运动，在水平方向做匀速直线运动，即水平地面上的垂直投影的运动速度大小等于v；在竖直方向上做自由落体运动，即竖直地面上的垂直投影的运动是匀加速运动。
故选BC。
5．（2023·重庆·高考真题）如图所示，桌面上固定有一半径为R的水平光滑圆轨道，M、N为轨道上的两点，且位于同一直径上，P为MN段的中点。在P点处有一加速器（大小可忽略），小球每次经过P点后，其速度大小都增加v0。质量为m的小球1从N处以初速度v0沿轨道逆时针运动，与静止在M处的小球2发生第一次弹性碰撞，碰后瞬间两球速度大小相等。忽略每次碰撞时间。求：
（1）球1第一次经过P点后瞬间向心力的大小；
（2）球2的质量；
（3）两球从第一次碰撞到第二次碰撞所用时间。

【答案】（1）；（2）3m；（3）
【详解】（1）球1第一次经过P点后瞬间速度变为2v0，所以
（2）球1与球2发生弹性碰撞，且碰后速度大小相等，说明球1碰后反弹，则
联立解得
，
（3）设两球从第一次碰撞到第二次碰撞所用时间为Δt，则
所以
6．（2024·江苏·高考真题）嫦娥六号在轨速度为v0，着陆器对应的组合体A与轨道器对应的组合体B分离时间为Δt，分离后B的速度为v，且与v0同向，A、B的质量分别为m、M。求：
（1）分离后A的速度v1大小；
（2）分离时A对B的推力大小。
【答案】（1）；（2）
【详解】（1）组合体分离前后动量守恒，取v0的方向为正方向，有
(m＋M)v0 = Mv＋mv1
解得
（2）以B为研究对象，对B列动量定理有
FΔt = Mv－Mv0
解得
7．（2024·湖南·高考真题）如图，半径为R的圆环水平放置并固定，圆环内有质量为mA和mB的小球A和B（mA>mB）。初始时小球A以初速度v0沿圆环切线方向运动，与静止的小球B发生碰撞。不计小球与圆环之间的摩擦，两小球始终在圆环内运动。
（1）若小球A与B碰撞后结合在一起，求碰撞后小球组合体的速度大小及做圆周运动所需向心力的大小；
（2）若小球A与B之间为弹性碰撞，且所有的碰撞位置刚好位于等边三角形的三个顶点，求小球的质量比。
（3）若小球A与B之间为非弹性碰撞，每次碰撞后的相对速度大小为碰撞前的相对速度大小的e倍（0