初中数学浙教版（2024）七年级上册（2024）5.5 一元一次方程的应用完美版ppt课件

这是一份初中数学浙教版（2024）七年级上册（2024）5.5 一元一次方程的应用完美版ppt课件，文件包含552一元一次方程的应用pptx、教案552一元一次方程的应用docx、学案552一元一次方程的应用docx等3份课件配套教学资源，其中PPT共32页， 欢迎下载使用。
1. 学生能够理解等长等积变形问题中的数量关系，并能准确设出未知数;2. 掌握运用一元一次方程解决等长等积变形问题的方法，提高解题能力;3. 通过解决实际问题，培养学生的数学思维和应用意识。
把一杯水倒入另一只杯中。请指出倒水过程中，哪些量发生了变化，哪些量保持不变。
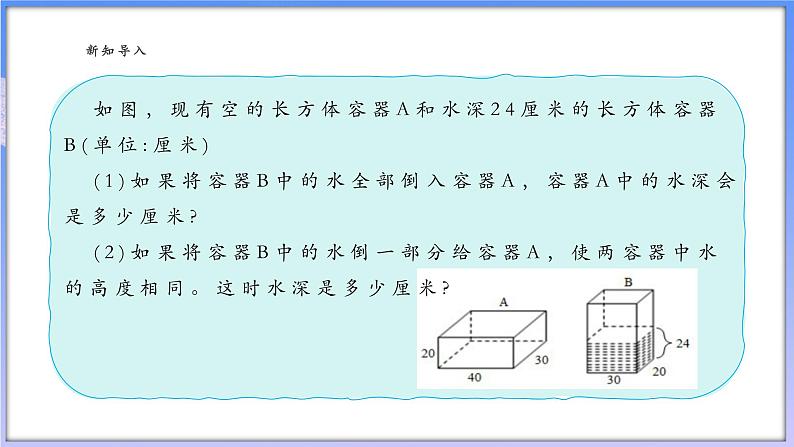
如图，现有空的长方体容器A和水深24厘米的长方体容器B(单位:厘米)(1)如果将容器B中的水全部倒入容器A，容器A中的水深会是多少厘米?(2)如果将容器B中的水倒一部分给容器A，使两容器中水的高度相同。这时水深是多少厘米?
等积(长)变形问题的关键：此类问题的关键在“等积”与“等长”上，是等量关系的所在，必须掌握常见几何图形的周长、面积、体积公式。 “等积变形”是以形状改变而体积不变为前提。“等长变形”是形状改变而周长不变为前提。
▶例3 某雕像的底面呈正方形，在其四周铺上花岗岩，形成一个边宽为3.2米的正方形框（如图中阴影部分）。已知铺这个框恰好用了144块边长为0.8米的正方形花岗岩（接缝忽略不计），问：该雕像的底面边长是多少米？
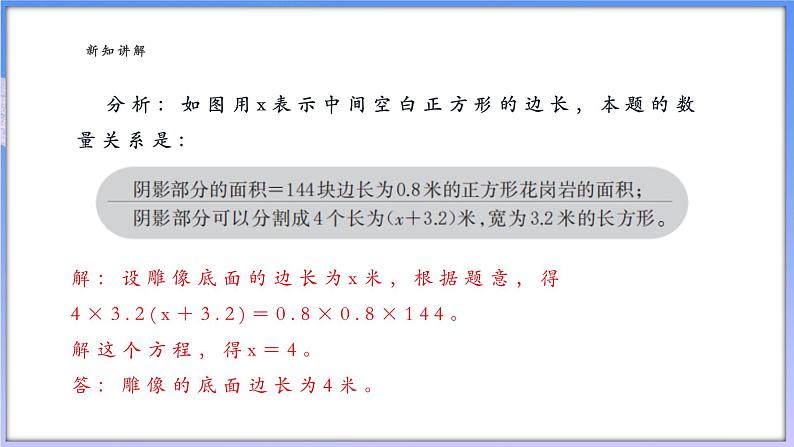
分析：如图用x表示中间空白正方形的边长，本题的数量关系是：
解：设雕像底面的边长为x米，根据题意，得4×3.2(x＋3.2)＝0.8×0.8×144。解这个方程，得x＝4。答：雕像的底面边长为4米。
在运用方程解决有关实际问题时，清楚地分辨量与量之间的关系，尤其是相等关系，是建立方程的关键。解题中的检验对确保答案的正确和合理很有帮助，但具体过程可以省略不写。
▶例4 如图用直径为200mm的钢柱锻造一块长、宽、高分别为300mm，300mm和80mm的长方体毛坯底板。问：应截取钢柱多少长（不计损耗，结果误差不超过1mm）？
【例1】一个长方形的周长是40cm,若将长减少8cm,宽增加2cm,长方形就变成了正方形,则正方形的边长为（ ）A.6cm B.7cm C.8cm D.9cm
B【解析】设正方形的边长为xcm,则长方形的长为(x+8)cm,宽为(x-2)cm。由题意得2(x+8+x-2)=40,解得x=7。故选B。
【例2】水结成冰,体积会增加10%,现有一块冰,体积是5500立方分米,融化成水后体积减少了_______立方分米。
500【解析】设这块冰融化成水后体积为x立方分米。依题意得(1+10%)x=5500,解得x=5000。故融化成水后体积减少了5500-5000=500(立方分米)。故答案为500。
【例4】用一根长10米的铁丝围成一个长方形，使得长方形的长比宽多1.2米，此时长方形的长是多少米？宽是多少米？
【解析】设长方形的宽为x米，则长为(x+1.2)米。依题意得：2(x+1.2+x)=10，解得x=1.9，所以x=1.2+1.9=3.1，答：长方形的长为3.1米，宽为1.9米。
【选做】5.如图(1)是一个盛有水的圆柱形玻璃容器的轴截面示意图,把甲、乙两根相同的玻璃棒垂直插入水中,高度与水面齐平。如图(2),先将甲玻璃棒竖直向上提起4cm,露出水面部分高度为5cm,保持甲玻璃棒离容器底部4cm不变,再将乙玻璃棒竖直向上提起6cm,发现乙玻璃棒仍有部分浸入水中,则乙玻璃棒露出水面部分的高度为_______cm。
【选做】6.根据以下素材,探索完成任务。
【解析】任务1:根据题意,可知设计部分的长为(330-2x)cm,宽为(220-2x)cm.任务2:因为设计的部分也是长方形,且长是宽的1.55倍,所以330-2x=1.55(220-2x),解得x=10,所以四周空白部分宽度是10cm。
知识点 等积(长)变形问题的关键：此类问题的关键在“等积”与“等长”上，是等量关系的所在，必须掌握常见几何图形的周长、面积、体积公式。“等积变形”是以形状改变而体积不变为前提。“等长变形”是形状改变而周长不变为前提。在运用方程解决有关实际问题时，清楚地分辨量与量之间的关系，尤其是相等关系，是建立方程的关键。解题中的检验对确保答案的正确和合理很有帮助，但具体过程可以省略不写。
【选做】1.把一根长100cm的木棍锯成两段,若使其中一段的长比另一段长的2倍少5cm,则锯出的木棍的长不可能为( )A.70cm D.35cm或65cm
A【解析】设一段长为xcm，另一段(2x-5)cm，则:x+(2x-5)=100cm,解得:x=35cm，所以2x-5=65(cm)所以锯出的木棍的长不可能为70cm，故选A。
【选做】2.用一根10cm长的铁丝围成一个三角形,然后把它改围成一个正方形,下列说法正确的是( )A.围成的图形的周长不变B.围成的图形的面积不变C.围成的图形的周长变长D.围成的图形的面积与周长都不变
A【解析】用一根10cm长的铁丝围的一个三角形的周长与改围成一个正形的周长都是10cm,即围成的图形的长不变;围成的一个三角形的面积与围的一个正方形的面积不相等。故选A.
【必做】3.要锻造直径为60mm，高为30mm的圆柱形毛坯，需截取直径为40mm的圆钢长是多少毫米？
【必做】4.有一段钢材可作一个底面直径8厘米，高9厘米的圆柱形零件。如果把它改制成高是12厘米的圆锥形零件，零件的底面积是多少平方厘米?
【必做】5.如图，某小学将一块梯形空地改成宽为30m的长方形运动场地，要求面积不变若在改造后的运动场地，小王、小李两人同时从点A出发，小李沿着长方形边顺时针跑小王则是逆时针跑，并且小王每秒比小李多跑2m，经过10秒钟他们相遇。(1)求长方形的长;(2)求小王、小李两人的速度。
【解析】(1)设长方形的长为x米。依题意得:(30+60)×30÷2=30×x解得:x=45答:长方形的长为45米。(2)设小李的速度是ym/s，则小王的速度是(y+2)m/s，由题意得:10(y+y+2)=(45+30)×2解得:y=6.5，则y+2=8.5.答:小李的速度是6.5m/s，则小王的速度是8.5m/s。
【选做】6.一个密封的玻璃缸，从里面量长12分米，宽是3分米，高是6分米，现在缸内的水深5分米。(1)制作一个这样的玻璃缸至少需要多少平方分米的玻璃?(2)这个玻璃鱼缸内装了多少升水?(图1)(3)如果将这个玻璃鱼缸竖起来放(图2)，那么鱼缸内水深多少分米?
【解析】(1)根据长方体的表面积公式得:S=(12×3+12×6+3×6)×2=(36+72+18)×2=126×2=252(平方分米)答:制作一个这样的玻璃缸至少需要252平方分米的玻璃。(2)根据长方体的体积公式:V=abh,得12×3×5=180(立方分米) 180立方分米=180升答:这个玻璃鱼缸内装了180升水。(3)根据(2)可知这个鱼缸里水的体积,竖起来放,体积不变,根据长方体的体积式:V=Sh,得180÷(3×6)=180-18=10(分米)答:鱼缸内水深10分米。
【拓展题】一个密封的长方体容器，里面长8分米，宽2分米，高4分米，已装了一部分水，水深2.5分米。(1)水与容器的接触面积是多少平方分米?(2)如果以这个长方体的右侧面为底面把长方体竖起来放在桌子上，这时水深是多少分米？