黑龙江省哈尔滨市松北区2024-2025学年九年级上学期期中考试数学试题

这是一份黑龙江省哈尔滨市松北区2024-2025学年九年级上学期期中考试数学试题，共10页。试卷主要包含了答题前，考生先将自己的“姓名”，选择题必须使用2B铅笔填涂，保持卡面整洁，不要折叠，证明，分别代入中，得等内容，欢迎下载使用。
考生须知：
1、本试卷满分为120分，考试时间为120分钟。
2、答题前，考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚，将“条形码”准确粘贴在条形码区域内。
3、请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题纸上答题无效。
4、选择题必须使用2B铅笔填涂：非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
5、保持卡面整洁，不要折叠、不要弄脏、弄皱，不准使用涂改液、刮纸刀。
第Ⅰ卷 选择题（共30分）（涂卡）
一、选择题（每题3分，计30分，每题只有一个正确的答案）
1.2024的倒数的相反数是（ ）
A.2024B.－2024C.D.
2.下列运算一定正确的是（ ）
A.a2＋a2＝a4B.C.D.
3.下列图标中是中心对称图形的是（ ）
A.B.C.D.
4.已知关于x的方程mx2－4x＋2＝0有两个不相等的实数根，则m的取值范围是（ ）
A.m＜2且m≠0B.m＜2C.m＞2且m≠0D.m＞2
5.如图，OA，OB是的两条半径，且OA⊥OB，点C在上，则∠ACB的度数为（ ）
A.45°B.35°C.25°D.20°
6.在平面直角坐标系中，将抛物线y＝2x2先向左平移1个单位长度，再向下平移3个单位长度后所得到的抛物线的解析式为（ ）
A.B.C.D.
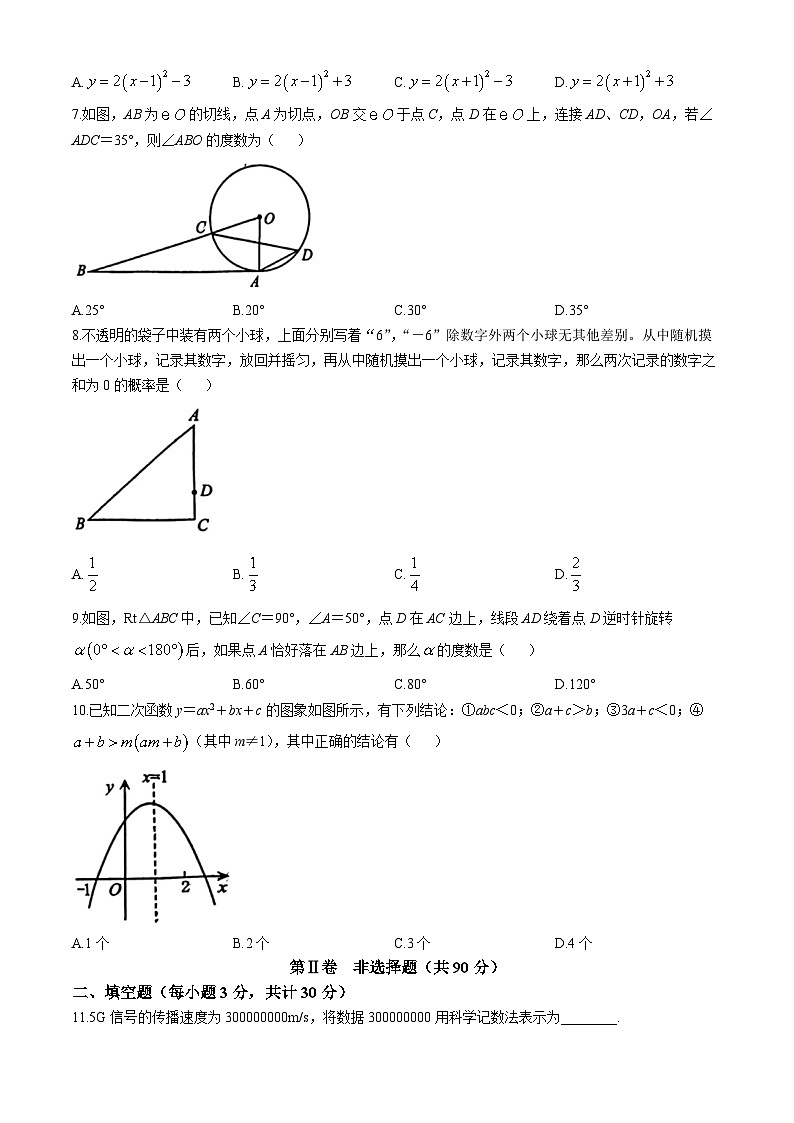
7.如图，AB为的切线，点A为切点，OB交于点C，点D在上，连接AD、CD，OA，若∠ADC＝35°，则∠ABO的度数为（ ）
A.25°B.20°C.30°D.35°
8.不透明的袋子中装有两个小球，上面分别写着“6”，“－6”除数字外两个小球无其他差别。从中随机摸出一个小球，记录其数字，放回并摇匀，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为0的概率是（ ）
A.B.C.D.
9.如图，Rt△ABC中，已知∠C＝90°，∠A＝50°，点D在AC边上，线段AD绕着点D逆时针旋转后，如果点A恰好落在AB边上，那么的度数是（ ）
A.50°B.60°C.80°D.120°
10.已知二次函数y＝ax2＋bx＋c的图象如图所示，有下列结论：①abc＜0；②a＋c＞b；③3a＋c＜0；④（其中m≠1），其中正确的结论有（ ）
A.1个B.2个C.3个D.4个
第Ⅱ卷 非选择题（共90分）
二、填空题（每小题3分，共计30分）
11.5G信号的传播速度为300000000m/s，将数据300000000用科学记数法表示为________.
12.在函数中，自变量x的取值范围是________.
13.若是关于x的一元二次方程，则m＝________.
14.计算的结果是________.
15.如图，OA为的半径，弦BC⊥OA于点P.若BC＝8，AP＝2，则的半径长为________.
16.三角形两边长为3和6，第三边是方程x2－6x＋8＝0的解，这个三角形的周长是________.
17.若二次函数y＝x2－6x＋3a的图象与x轴有且只有一个交点，则a的值为________.
18.如图，AB是的直径，点C在上，点D在优弧BAC上，若∠CAB＝20°，则∠ADC的度数是________.
19.一个扇形的面积是13πcm2，半径是6cm，则此扇形的圆心角是________度.
20.如图，正方形OABC的顶点B在抛物线y＝x2的第一象限的图象上，若点B的横坐标与纵坐标之和等于6，则对角线AC的长为________.
三、解答题（其中21－22题各7分，23－24题各8分，25－27题各10分，共计60分）
21.（本题7分）先化简，再求代数式的值，其中.
22.（本题7分）如图，方格纸中每个小正方形的边长均为1，线段AB和线段CD的端点均在小正方形的顶点上.
（1）在图中画出线段AB绕着点B顺时针旋转90°的线段BE，点E在小正方形的顶点上；
（2）在图中画出以CD为边的等腰三角形CDG，点G在小正方形的顶点上，且△CDG的周长为.连接AE、EG，请直接写出点G到AE的距离是多少.
23.（本题8分）某学校食堂为学生提供了A，B，C，D四种套餐，为了解学生对这四种套餐的喜好情况，单位随机抽取若干名学生进行“你最喜欢哪一种套餐（必选且只选一种）”问卷调查.根据调查结果绘制了条形统计图和扇形统计图，部分信息如下：
调查结果的条形统计图 调查结果的扇形统计图

（1）在这次随机抽样中，一共调查了多少名学生？
（2）通过计算补全条形图，并求出扇形统计图中C的扇形圆心角的度数；
（3）若该学校现有在校学生1500人，请你估计该学校喜欢D套餐的学生一共有多少名.
24.（本题8分）如图，AB是半圆的直径，C，D是半圆上不同于A，B的两点，AD＝BC，AC与相交于点F.BE是半圆所在圆的切线，与AC的延长线相交于点E.
（1）求证：△CBA≌△DAB；
（2）若BE＝BF，写出四个图中等于2CE的线段.
25.（本题10分）某商场服装部在销售中发现：某品牌秋装平均每天可售出20件，每件盈利40元.为了迎接“十·一”国庆节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存.经市场调查发现：如果每件秋装降价1元，那么平均每天就可多售出2件.
（1）要想平均每天销售这种秋装盈利1200元，那么每件秋装应降价多少元？
（2）每件秋装降价多少元时，每天销售这种秋装的利润最高？最高利润是多少？
26.（本题10分）如图1，点A、C、E、G在上，弧AE＝弧CG；

图1 图2
（1）求证：AG＝CE；
（2）如图2，点F在上，连接AE、EF，延长AG、CE交于点B，作FH⊥EC延长线于点H，若∠AEF＝90°，∠CAG＝45°，求证：BE＝CH；
（3）在（2）的条件下，若EC＝4，∠CEF＝15°，求FH的长.
27.（本题10分）如图1，抛物线过点O（0，0）和A（6，0）.

图1 图2 图3
（1）求抛物线的解析式；
（2）如图2，点B是抛物线的顶点，点D是x轴下方抛物线上的一点，连接OD，且OD平分∠AOB，抛物线的对称轴交x轴于点C，交线段OD于点E，点F是线段OB上的动点（点F不与点O和点B重合），连接EF、OB，设点F的横坐标为t，△BEF的面积为s，求s关于t的函数关系式（不用写出自变量的取值范围）；
（3）如图3，在（2）的条件下，当s＝3时，将△BEF沿EF折叠，点B的对应点为点，求点的坐标.
2024－2025学年度上学期九年级期中考试题
数学试卷参考答案
1－5 DCBAA 6－10 CBACB
11、 12、x≠7 13、1 14、 15、5 16、13 17、3 18、110°或70° 19、130 20、
21、解：原式
，…………4'
，
原式…………3'
22、解：（1）如图，线段BE即为所求 （2）如图，△CDG即为所求，点G到AE的距离是.
…………7'
23、解：（1）84÷35%＝240（名）
答：在这次林随机抽样中，一共调查了240名学生。…………2'
（2）在抽取的240人中最喜欢A套餐的人数为240×25%＝60（人），
则最喜欢C套餐的人数为240－（60＋84＋24）＝72（人），
∴扇形统计图中“C”对应扇形的圆心角的大小为，补全条形图如图所示。……4'
（3）（名）
答：估计该学校喜欢D套餐的学生一共有150名.…………2'
24、（1）证明：∵AB是半圆的直径，
∴∠ACB＝∠ADB＝90°，
在Rt△CBA与Rt△DAB中，，
∴Rt△CBA≌Rt△DAB（HL）；…………4'
（2）解：分别是线段AF、BE、EF、BE。…………4'
25、解：（1）设要想平均每天销售这种秋装盈利1200元，那么每件秋装应降价x元，，
解得，，x2＝20
当x＝20时，卖出的多，库存比x＝10时少，
答：要想平均每天销售这种秋装盈利1200元，那么每件秋装应降价20元；…………5'
（2）设每件秋装降价x元，利润为y元，
，
∵a＝－2＜0，
∴当x＝15时，y取得最大值，此时y＝1250，
答：每件秋装降价15元时，每天销售这种秋装的利润最高，最高利润是1250元.…………5'
26、（1）证明：∵连接OA、OG、OE、OC，
∴∠AOG＝∠COE
∴AG＝CE；…………2'
（2）证明：
∴由（1）可知AE＝EF，∠CAG＝∠ACE
∵∠CAG＝45°
∴∠ACE＝45°
∴∠ABC＝90°，AB＝BC
∵∠AEF＝90°
∴∠AEB＋∠FEH＝90°
∠AEB＋∠BAE＝90°
∴∠BAE＝∠FEH
在△ABE和△EHF中
连接
△ABE≌△EHF
∴AB＝EH
∴BC＝EH
∴BE＝CH.…………4'
（3）解：连接OE、OC、AF
∵∠CAG＝45°，∠BAE＝∠CEF＝15°，
∴∠CAE＝30°
∴∠COE＝2∠CAE＝60°
∴OE＝OC＝CE＝4
∵∠AEF＝90°，AE＝EF
∴AF是⊙O的直径，即AF＝2OE＝8
在Rt△AEF中
AF2＝AE2＋EF2
∵AE＝EF
由（2）知BE＝CH＝FH，设CH＝FH＝x
在Rt△EFH中
EF2＝FH2＋EH2
∵x＞0
，即.…………4'
27、（1）解：把点C（0，0）和A（6，0）分别代入中，得：
，
解得，
∴抛物线的解析式…………2'
（2）解：
，
∴顶点，对称轴与x轴的交点C（3，0），
∴OC＝3，，
在Rt△OCB中，作斜边上的中线CM
∵OB2＝OC2＋BC2
∴OB＝6
∴△COM是等边三角形
∴∠COB＝60°，
∵OD平分∠AOB，
∴∠COE＝30°
在Rt△COE中，OE2＝OC2＋EC2
作FN⊥BC于N
∵点F的横坐标为t，
∴FN＝3－t
即…………4'
（3）解：当s＝3时，代入，得
∵∠OBC＝30°
∴∠BFE＝∠BEF＝75°
∵将△BEF沿EF折叠，
，
，即轴，设垂足为P
在Rt△POF中，
∵∠OFP＝30°
∵OF2＝OP2＋PF2

∴点的坐标为…………4'