

广东省广州市海珠区中山大学附属实验学校2024-2025学年九年级上学期期中数学试题与答案
展开
这是一份广东省广州市海珠区中山大学附属实验学校2024-2025学年九年级上学期期中数学试题与答案,共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(共10小题,满分30分,每小题3分)
1.我国古代典籍《周易》用“卦”描述万物的变化.如图为部分“卦”的符号,其中是中心对称图形的是( )
A.B.C.D.
2.的半径为3,点..在外,点到圆心的距离为,则需要满足的条件( )
A.B.C.D.无法确定
3.用配方法解一元二次方程时,配方正确的是( )
A.B.C.D.
4.如图,在中,为直径,,为圆上的点,若,则..的大小为( )
A.51°B.49°C.40°D.39°
5.在平面直角坐标系中,抛物线如图所示,则关于的方程的根的情况为( )
A.有两个不相等的实数根B.没有实数根
C.有实数根D.有两个相等的实数根
6.抛物线的顶点坐标是( )
A.B.C.D.
7.若关于的一元二次方程有一个根为1,则的值为( )
A.3B.0C.D.
8.如图,将绕点顺时针方向旋转到的位置,使得点,,在同一条直线上,,那么旋转角等于( )
A.65°B.100°C.115°D.120°
9.某公司今年10月的营业额为2500万元,按计划第四季度的总营业额要达到9100万元,求该公司11、12两个月营业额的月均增长率,设该公司11、12两个月营业额的月均增长率为,则根据题意可列的方程为( )
A.B.
C.D.
10.当时,函数与的图象有且只有一个交点,其中为常数.则的取值为( )
A.或B.C.D.
二、填空题(共6小题,满分18分,每小题3分)
11.若关于的一元二次方程有整数根,则整数的值可以是______(写出一个即可).
12.在平面直角坐标系中,将抛物线向下平移1个单位,得到的抛物线表达式为______.
13.一个等腰三角形的底边长是6,腰长是一元二次方程的一个根,则此三角形的周长是______.
14.如图,、是的切线,点、为切点,是的直径,,则的大小是______度.
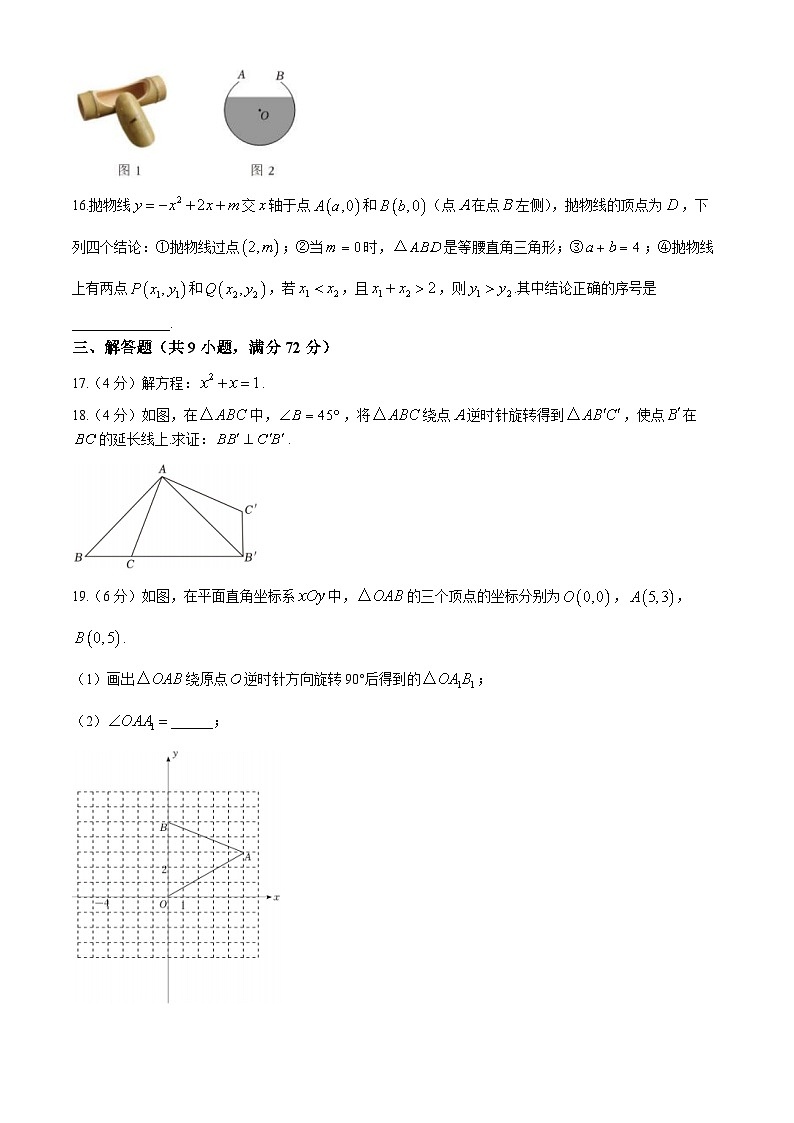
15.“青山绿水,畅享生活”,人们经常将圆柱形竹筒改造成生活用具,图1所示是一个竹筒水容器,图2为该竹筒水容器的截面.已知截面的半径为10cm,开口宽为12cm,这个水容器所能装水的最大深度是______cm.
16.抛物线交轴于点和(点在点左侧),抛物线的顶点为,下列四个结论:①抛物线过点;②当时,是等腰直角三角形;③;④抛物线上有两点和,若,且,则.其中结论正确的序号是______________.
三、解答题(共9小题,满分72分)
17.(4分)解方程:.
18.(4分)如图,在中,,将绕点逆时针旋转得到,使点在的延长线上.求证:.
19.(6分)如图,在平面直角坐标系中,的三个顶点的坐标分别为,,.
(1)画出绕原点逆时针方向旋转90°后得到的;
(2)______;
20.(6分)如图,用篱笆围成一块矩形花圃,该花圃一侧靠墙,而且有一道隔栏(隔栏也用篱笆制作),已知所用篱笆的总长为24m,花圃的面积为,墙的最大可用长度为10m,求边的长.
21.(8分)如图,为的直径,交于点,为上一点,延长交于点,延长至,使,连接.
(1)求证:为的切线;
(2)若且,求的半径.
22.(10分)如图,在中,,.
(1)尺规作图:将绕点顺时针旋转得到,使得点的对应点在的延长线上(保留作图痕迹,不写作法);
(2)在(1)的条件下,连接,判断点与直线的位置关系,并说明理由.
23.(10分)在平面直角坐标系中,点,点在抛物线上.设抛物线的对称轴为直线.
(1)当时,
①直接写出与满足的等量关系;②比较,的大小,并说明理由;
(2)已知点在该抛物线上,若对于,都有,求的取值范围.
24.(12分)如图1所示,等边三角形内接于圆,点是劣弧上任意一点(不与重合),连接、、,求证:.
【初步探索】小明同学思考如下:将与点顺时针旋转60°到,使点与点重合,可得、、三点在同一直线上,进而可以证明为等边三角形,根据提示,解答下列问题:
(1)根据小明的思路,请你完成证明.
(2)若圆的半径为8,则的最大值为_____________(直接写答案).
【类比迁移】如图2所示,等腰内接于圆,,点是弧上任一点(不与、重合),连接、、,若圆的半径为8,试求周长的最大值.
【拓展延伸】如图3所示,等腰,点、在圆上,,圆的半径为8,连接,则的最小值为_____________(直接写答案).
25.(12分)正方形的顶点在某抛物线上,称该正方形为该抛物线的“悬正方形”.若直线与“悬正方形”以为端点的一边相交,且点到直线的距离为,则称直线为该正方形的“悬割线”.
已知抛物线,其中,,,以为边作正方形(点在点的下方).
(1)证明:正方形是抛物线的“悬正方形”;
(2)判断正方形是否还可能是抛物线的“悬正方形”,并说明理由;
(3)若直线是正方形的“悬割线”,现将抛物线及正方形进行相同的平移,是否存在直线为平移后正方形的“悬割线”的情形?若存在,请探究抛物线经过了怎样的平移;若不存在,请说明理由.
2024学年第一学期期中考试模拟考试卷参考答案与试题解析
一、选择题(共10小题,满分30分,每小题3分)
2.解:当时,;当时,;
当时,函数的图象如图一所示:
函数是由函数向上或向下平移得到的,
由图象可知,①时,当时,函数与的图象有且只两个一个交点,不符合题;
②把函数向下平移到过点时,得.解得,
在此过程中,函数与的图象有且只有一个交点;
③把函数向上平移到图象位置时,函数与的图象有且只有一个交点,此时,即,,解得.
综上所述,当或时,函数与的图象在范围内有且只有一个交点.故选:A.
二、填空题(共6小题,满分18分,每小题3分)
11.4(答案不唯一). 12.. 13.14. 14.40. 15.18cm. 16.①②④.
16.解:①把代入得,,抛物线过点,故①正确;
②当时,抛物线与轴的两个交点坐标分别为、,对称轴为,
是等腰直角三角形,故②正确;
③抛物线交轴于点和(点在点左侧),
、是方程的两个根,,故③错误;
④观察二次函数图象可知:当,且,则.故④正确.故答案为:①②④.
三、解答题(共9小题,满分72分)
17.解:,
,,,
,
,,.
18.解:绕点逆时针旋转得到,,,
而点在的延长线上.,,
,.
19.解:(1)如图,即为所求.
(2),,.故答案为:45°.
20.解:设边边的长为,
由题意得:,
解得:(不符合题意,舍去),,
答:边的长为5m.
21.解:(1)证明:如图,连接,
,,
,,
,,,
即,,是半径,为的切线;
(2)解:设的半径,则,,
在中,由勾股定理得,,,
解得,或(舍去),
的半径为3.
22.解:(1)如图,为所作;
(2)点在直线上.理由如下:
绕点顺时针旋转得到,,,
,
,,
,
,
,
点、、共线,即点在直线上.
23.解:(1)①,
;
②抛物线中,,抛物线开口向上,
点,点在抛物线上,对称轴为直线,
点到对称轴的距离大于点到对称轴的距离,
;
(2)由题意可知,点在对称轴的左侧,点,在对称轴的右侧,
,都有,点到对称轴的距离大于点到对称轴的距离,
,
解得,
的取值范围是.
24.解:初步探索:
(1)证明:由旋转得,,,,
,,
、、三点在同一条直线上,,
是等边三角形,,,
是等边三角形,,;
(2)是的弦,且的半径为8,
当经过圆心,即是的直径时,此时的值最大,最大值为16,
的最大值是16,故答案为:16;
类比迁移:如图2,
,,是的直径,且圆心在上,,,
将绕点顺时针旋转90°到,使点与点重合,则,,,
,,、、三点在同一条直线上,
,,
当经过圆心,即是的直径时,此时的值最大,最大值为16,
的最大值为,的最大值为,
周长的最大值是;
拓展延伸:如图3,连接,将线段绕点逆时针旋转90°到,连接,
,,,
连接、,
,,
,,,
,,,的最小值为,
故答案为:.
25.证明:(1)当时,
,
则点在抛物线上,故正方形是抛物线的“悬正方形”;
(2)正方形不可能是抛物线的“悬正方形”,理由如下:
假设点在抛物线上,则当时,,则,
整理得,解得,
与矛盾,假设不成立,所以点不在抛物线上,
故正方形不可能是抛物线的“悬正方形”;
解:(3)假设存在直线为平移后正方形的“悬割线”的情形,则平移后,正方形是抛物线的“悬正方形”,
抛物线及正方形进行相同的平移,平移前,正方形是抛物线的“悬正方形”,则点在抛物线上,
,,轴,
,,
在正方形中,,,则,
点在抛物线上,,
解得,(不合题意,舍去),,
那么平移前,,,,
直线与轴,轴分别交于,,,
直线与轴夹角为45°,
因为平移前,直线是正方形的“悬割线”,如图,设直线与,分别交于点,,
轴,,
在正方形中,,,
则,,
,,,,
点在直线上,,
设点平移后的坐标为,设直线与平移后正方形的边交于点,
如图,同理可得,则,
点在直线上,,,
抛物线及正方形进行相同的平移,
要使直线为平移后正方形的“悬割线”,则抛物线向右平移个单位长度,向上平移个单位长度,其中为任意实数.
相关试卷
这是一份广东省广州市海珠区中山大学附中2023-2024学年九年级上学期期中数学试卷,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省广州市海珠区中山大学附属中学2023-2024学年七年级下学期期中数学试题,文件包含广东省广州市海珠区中山大学附属中学2023-2024学年七年级下学期期中数学试题原卷版docx、广东省广州市海珠区中山大学附属中学2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
这是一份2023-2024学年广东省广州市海珠区中山大学附中九年级(上)期中数学试卷,共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









