

上海市闵行区六校联考2024-2025学年高一上学期期中考试数学试卷(含答案)
展开这是一份上海市闵行区六校联考2024-2025学年高一上学期期中考试数学试卷(含答案),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题
1.设l,m,n是不同的直线,m,n在平面内,则“且”是“”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
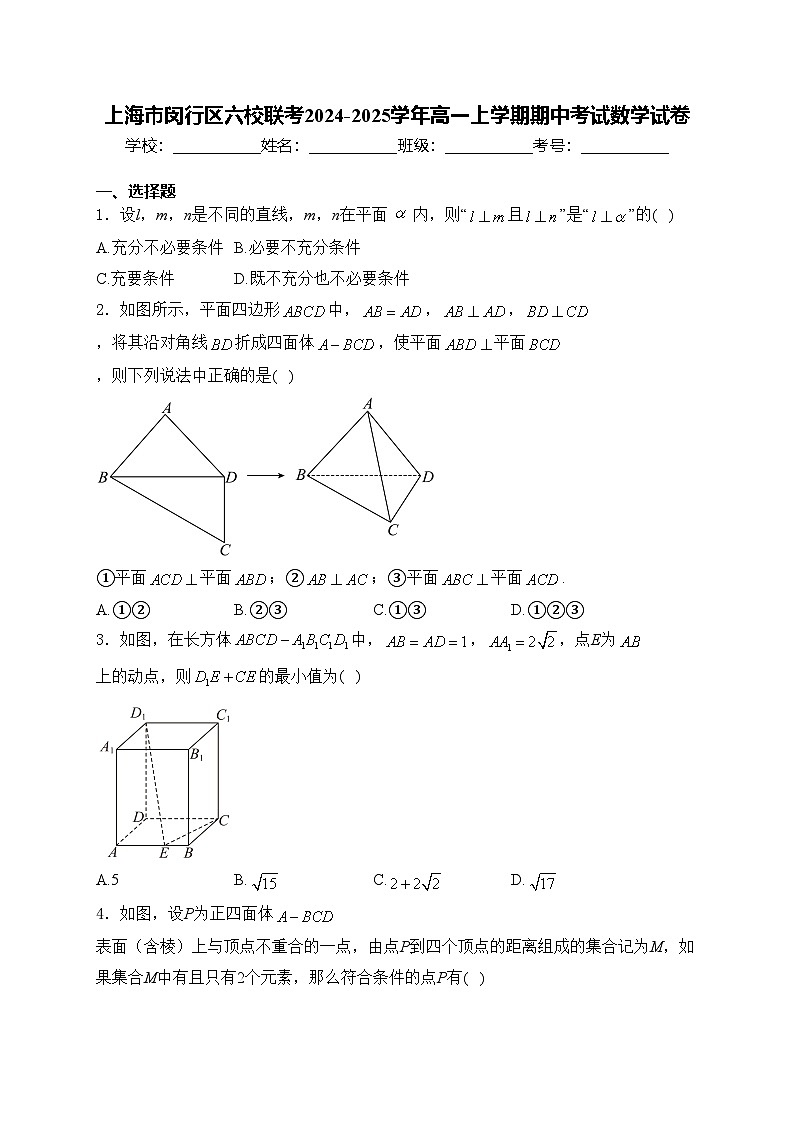
2.如图所示,平面四边形中,,,,将其沿对角线折成四面体,使平面平面,则下列说法中正确的是( )
①平面平面;②;③平面平面.
A.①②B.②③C.①③D.①②③
3.如图,在长方体中,,,点E为上的动点,则的最小值为( )
A.5B.C.D.
4.如图,设P为正四面体表面(含棱)上与顶点不重合的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )
A.4个B.6个C.10个D.14个
二、填空题
5.如果一条直线和两条异面直线中的一条平行,那么它和另一条直线的位置关系是________.
6.若平面,直线,直线,则点M与l的位置关系为____________.
7.正方体中,异面直线与所成角的大小为_________.
8.在正方体中,,则直线到平面的距离为________.
9.的斜二测直观图如图所示,则的面积是________.
10.以下四个命题中,真命题是(只填真命题的序号)________.
①若a,b是两条直线,且,则a平行于经过b的任何平面;
②若直线a和平面满足,则a与内的任何直线平行;
③若直线a,b和平面满足,,则;
④若直线a,b和平面满足,,,则.
11.一个圆台的两个底面半径分别为1和2,高为1,则该圆台的体积为________.
12.已知圆锥的表面积为,其侧面展开图是一个半圆.则圆锥的高为________.
13.正方体的棱长为2,E是棱的中点,则平面截该正方体所得的截面面积为________.
14.如图,求一个棱长为的正四面体的体积,可以看成一个棱长为1的正方体截去四个角后得到,类比这种方法,一个三对棱长相等的四面体,其三对棱长分别为,,,则此四面体的体积为________.
15.某同学在参加魔方实践课时,制作了一个工艺品,如图所示,该工艺品可以看成是一个球被一个棱长为的正方体的六个面所截后剩余的部分,(球心与正方体的中心重合),若其中一个截面圆的周长为,则该球的表面积是________.
16.在我国古代数学名著《九章算术》中,将四个面都是直角三角形的四面体称之为鳖臑,在鳖臑中,平面,且有,,,点P是上的一个动点,则的面积的最小值为________.
三、解答题
17.如图,已知E,F,G,H分别是正方体的棱,,,的中点,且与相交于点Q.
(1)求证:点Q在直线上;
(2)求证:与是异面直线.
18.在如图所示的圆柱中,是底面直径,是圆柱的母线,且.设C是底面圆周上的动点.
(1)求圆柱的表面积和体积;
(2)当二面角的大小为时,求点C到平面的距离.
19.我国古代数学名著《九章算术》中记载了有关特殊几何体的定义:“阳马”是指底面为矩形,一侧棱垂直于底面的四棱锥;“堑堵”是指底面是直角三角形,且侧棱垂直于底面的三棱柱.如图所示,在堑堵中,若,.
(1)求证:四棱锥为阳马;
(2)若直线与平面所成的角为时,求该堑堵的体积.
20.已知平面,平面,为等边三角形,,,F为的中点.
(1)求证:平面;
(2)求证:平面平面;
(3)求直线和平面所成角的正弦值.
21.在棱长均为2的正三棱柱中,E为的中点.过的截面与棱,分别交于点F,G.
(1)若F为的中点,试确定点G的位置,并说明理由;
(2)在(1)的条件下,求截面与底面所成锐二面角的正切值;
(3)设截面的面积为,面积为,面积为,当点F在棱上变动时,求的取值范围.
参考答案
1.答案:B
解析:若且,当时,直线l可以与平面平行,此时,不能推出,
若,m,n是平面内两条不同的直线,则,,
所以“且”是“”的必要不充分的条件.
故选:B
2.答案:D
解析:平面平面,平面平面,,平面,
平面,又平面,
平面平面,故①正确;
平面平面,平面平面,,平面,平面,平面,,故②正确;
平面,平面,平面平面,故③正确;
故选:D
3.答案:D
解析:将绕翻折到与共面,平面图形如下所示:
连接,则的长度即为的最小值,
因为,,所以,
所以,所以,即的最小值为.
故选:D
4.答案:C
解析:分以下两种情况讨论:(1)点P到其中两个点的距离相等,到另外两点的距离分别相等,且这两个距离不等,此时点P位于正四面体各棱的中点,符合条件的有6个点;
(2)点P到其中三个点的距离相等,到另外一点的距离与它到其它三点的距离不相等,此时点P在正四面体各侧面的中心点,符合条件的有4个点,故选C.
5.答案:异面或相交
解析:如果一条直线和两条异面直线中的一条平行,
那么它和另一条直线的位置关系是异面或相交.
故答案为:异面或相交
6.答案:
解析:因为,
所以直线a,直线b,
因为直线,直线,
所以平面,平面,
又平面,
所以.
故答案为:.
7.答案:/
解析:正方体中,,因此异面直线与所成的角或其补角,
而,,因此.
所以异面直线与所成角的大小为.
故答案为:.
8.答案:2
解析:根据正方体的性质可知,.
又平面,平面,
所以,平面.
所以,点A到平面的距离,即等于直线到平面的距离.
又平面,所以点A到平面的距离即为.
所以,直线到平面的距离为2.
故答案为:2.
9.答案:4
解析:依题意,由斜二测画法规则知,的底边,
边上的高,所以的面积是.
故答案为:4.
10.答案:④
解析:对于①,当经过b的平面也经过a时,不成立,故①为假命题;
对于②,a与内的直线平行或异面,故②为假命题;
对于③,直线a与b三种位置关系都有可能,故③也为假命题;
对于④,因为,过a作平面交于直线c,则,
又因为,所以,而,,所以.故④为真命题.
故答案为:④
11.答案:/
解析:由圆台的两个底面半径分别为1和2,高为1,得该圆台的体积.
故答案为:
12.答案:
解析:设圆锥的底面半径为r,母线长为l,高为h,
由于圆锥侧面展开图是一个半圆,
故有,
即圆锥母线长为,
又圆锥的表面积为,
解得,所以,
所以圆锥的高为.
故答案为:.
13.答案:
解析:如图所示,
设F为的中点,连接,.,设G为的中点,连接,,
由且,得是平行四边形,则且,
又且,得且,则A,E,,F共面,
故平面截该正方体所得的截面为.
又正方体的棱长为2,
所以,,,,
故的面积为.
故答案为:
14.答案:2
解析:设四面体所在的长方体棱长分别为a,b,c,则,解得,所以四面体的体积,故答案为2.
15.答案:
解析:设球心为O,作出过球心的截面图如图所示,则,
由截面圆的周长为,得,,
球的半径是.
所以该球的表面积为.
故答案为:.
16.答案:
解析:作图如下:
作于Q,于M,
连接,在鳖臑中,平面,
且有,,,
所以,,易得,,,
又,故平面,
所以,,,
即,,
所以.
设,则,因为,
所以,
当时,
最小为.
因为,
所以最小为时,
有最小值为.
故答案为:
17.答案:(1)证明见解析;
(2)证明见解析
解析:(1)平面平面,
由于平面,平面,
所以,也即点Q在直线上.
(2)假设与不是异面直线.
则与是共面直线,又E在直线外,
则过E与直线有唯一平面,所以可得平面,
这与F在平面外矛盾,故与是异面直线.
18.答案:(1)表面积为,体积为;
(2)
解析:(1)由题意可知,圆柱的底面半径为1,高为2,
则该圆柱的表面积为,体积为.
(2)因为平面,平面,则,
因为是底面直径,C是底面圆周上的动点,由题意可知,C与A、B不重合,所以,,
因为,平面,所以,平面,
因为平面,则,
所以,二面角的平面角为,即,
因为平面,平面,则,
所以,,则,
则,
,
又因为,
设点C到平面的距离为d,则,解得,因此,点C到平面的距离为.
19.答案:(1)证明见解析;
(2)
解析:(1)由题意在堑堵中,底面,
由底面,底面,
所以,,
在三棱柱中,四边形为平行四边形,
所以平行四边形为矩形,又,
又,平面,所以平面,
所以四棱锥为阳马.
(2)由(1)知平面,所以斜线在平面的射影为,
所以直线与平面所成的角为,
在中,,所以,
在中,,所以,
又,所以在中,,
所以堑堵的体积为:.
20.答案:(1)证明见解析;
(2)证明见解析;
(3)
解析:(1)取的中点G,连接、.
F为的中点,且.
平面,平面,
,.
又,.
四边形为平行四边形,则.
平面,平面,
平面.
(2)为等边三角形,F为的中点,.
平面,平面,.
,所以,,
又,平面,
平面.
平面,平面平面.
(3)在平面内,过F作于H,连接.
平面平面,平面平面,平面,
平面.
为和平面所成的角.
因,,则,,
在中,,
直线和平面所成角的正弦值为.
21.答案:(1)点G为棱上靠近点的三等分点,理由见解析;
(2);
(3)
解析:(1)在平面内延长,相交于点P,则平面,又平面,
则有平面平面,,即A,G,P三点共线.
因为E为的中点,F为的中点,所以,所以,又因为,所以,
所以,即点G为棱上靠近点的三等分点.
(2)在平面内延长,相交于点Q,
连接,则平面平面,
在平面内作于点M,则平面ABC,
又平面,所以,
在平面内作于点N,连接,
又平面,,所以平面,
平面,所以,
所以为截面与底面所成锐二面角的平面角.
在中,作于点H,,,,,,,
由余弦定理,则,
,可得,所以,
又,所以,
故截面与底面所成锐二面角的正切值为.
(3)设,则,.
设的面积为S,所以,
又因为,所以,且,
故,令,则,
设,
当时,,
,,,则,即,
所以在上单调递减,
所以,,所以,
所以.
相关试卷
这是一份上海市闵行区2024-2025学年高一上学期期中考试数学试卷,共13页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份上海市闵行区六校联合教研2024-2025学年高三上学期数学期中考试数学试卷(无答案),共4页。
这是一份上海市闵行区六校联考2024-2025学年高一上学期10月期中考试数学试题(无答案),共5页。












